41. 数据流中的中位数

剑指 Offer 41. 数据流中的中位数

295.数据流的中位数

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。
• double findMedian() - 返回目前所有元素的中位数。

示例 1：

输入：
[“MedianFinder”,“addNum”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[1],[2],[],[3],[]]
输出：[null,null,null,1.50000,null,2.00000]

示例 2：

输入：
[“MedianFinder”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[2],[],[3],[]]
输出：[null,null,2.00000,null,2.50000]

限制：

• 最多会对 addNum、findMedian 进行 50000 次调用。

注意：本题与主站 295 题相同：https://leetcode-cn.com/problems/find-median-from-data-stream/

解题思路

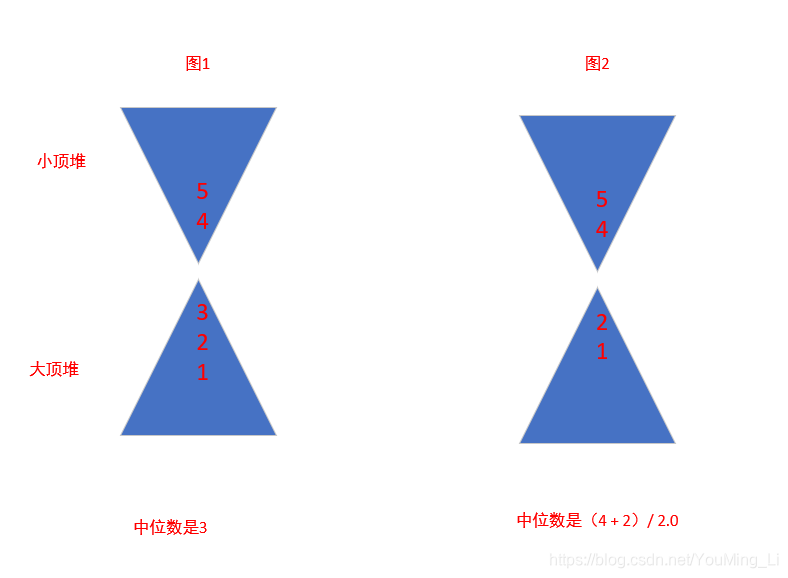
我们可以用两个堆来做，堆也就是优先级队列，如下图：我们用一个大顶堆来存数据流中较小的数，而用小顶堆来存数据流中较大的数，那么我们就有

• 如果数据数据流中元素个数为奇数，中位数便是大顶堆的堆顶元素，下图1
• 如果数据数据流中元素个数为偶数，中位数便是（大顶堆的堆顶元素 + 小顶堆的堆顶元素）/ 2.0,下图2
  

那么当数据流中有新数据进来时，我们要如何维护这两个堆呢？

很简单，我想通过上图大家也发现了，从下往上看的话(注意:这里是为了描述方便以及容易理解才将两个堆画成图示样子的，实际两个堆是完全独立的)，两个堆中的元素刚好是有序的，这也是为什么堆顶的元素就是中位数的原因，因为在中间位置嘛，所以我们首先要维护的就是有序，即让两个堆中的元素有图中所示一样的关系。

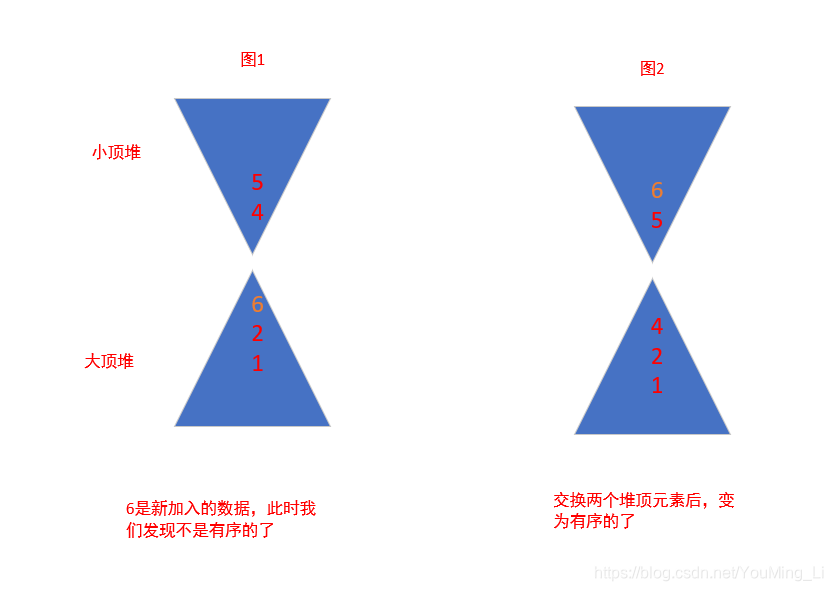
1. 我们可以每次新增元素时都放入大顶堆中，然后比较两个堆顶的元素，如果大顶堆的堆顶元素比小顶堆的堆顶元素大，则不符合有序了，如下图1，此时只需要交换两个堆顶的元素使之有序即可,下图2。
   

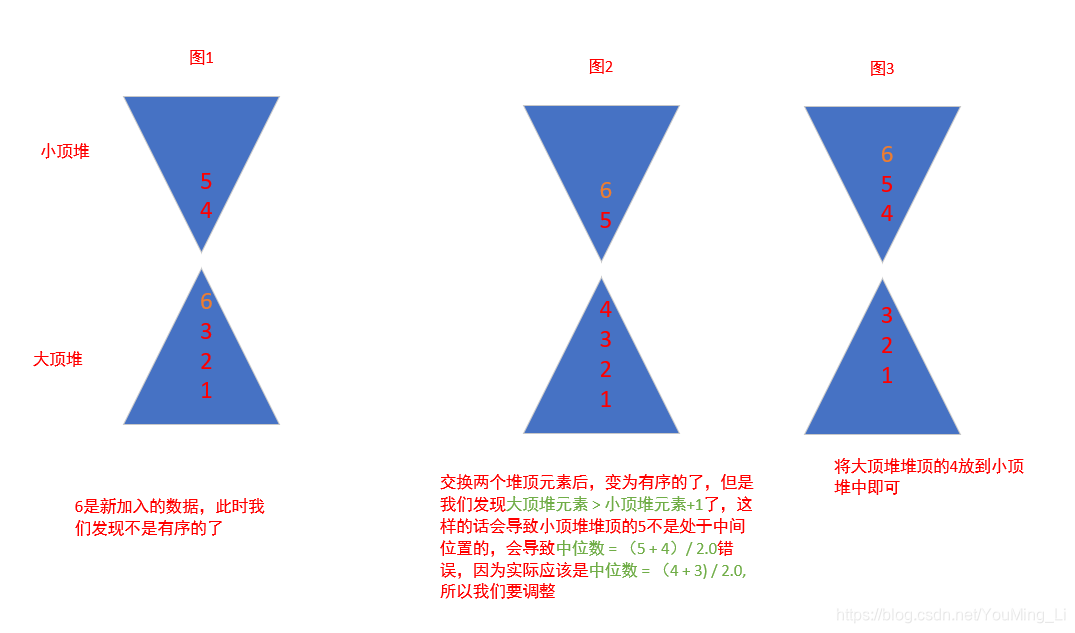
2. 由于要保证两个堆顶的元素处于中间位置，因此两个堆中的元素个数最多只能相差1，又我们每次都是将新数据插入大顶堆，所以为了维护解题思路下面奇数偶数时所说的求中位数方法一直正确，我们需要每次插入元素后都判断一下是否大顶堆中的元素个数是否不止比小顶堆中元素个数多1了，如果是，则应该调整，将大顶堆堆顶元素放入小顶堆,如下图。

Java代码

class MedianFinder {
    Queue<Integer> minQueue;
    Queue<Integer> maxQueue;

    /** initialize your data structure here. */
    public MedianFinder() {
        minQueue = new PriorityQueue<>();
        maxQueue = new PriorityQueue<>(new Comparator<Integer>(){
                @Override
                public int compare(Integer o1,Integer o2){
                    return o2 - o1;
                }
        });
    }
    
    public void addNum(int num) {
        maxQueue.add(num);
        if(!minQueue.isEmpty() && maxQueue.peek() > minQueue.peek()){
            int temp1 = maxQueue.poll();
            int temp2 = minQueue.poll();
            maxQueue.add(temp2);
            minQueue.add(temp1);
        }
        if(maxQueue.size() > minQueue.size() + 1){
            int temp = maxQueue.poll();
            minQueue.add(temp);
        }
    }
    
    public double findMedian() {
        int count = minQueue.size() + maxQueue.size();//数据流中当前共有多少数
        if((count & 1) != 0){//奇数
            return maxQueue.peek();
        }else{//偶数
            //注意需要返回的是double类型，故除2.0，写成2的话是整数除法，返回int型
            return (maxQueue.peek() + minQueue.peek()) / 2.0;
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */