Attention Rollout

最新推荐文章于 2025-12-11 21:18:03 发布

翻译最新推荐文章于 2025-12-11 21:18:03 发布 · 3.4k 阅读

4 ·

CC 4.0 BY-SA版权

原文链接：https://arxiv.org/pdf/2005.00928.pdf

文章标签：

#计算机视觉 #人工智能 #自然语言处理

Transformer 专栏收录该内容

3 篇文章

订阅专栏

本文探讨Transformer模型中Attention Rollout方法，揭示了随着模型加深，注意力模式的演变趋势，并通过Input Ablation实验验证了注意力权重的解释性。通过Attention Rollout计算机制，研究了信息如何在编码层级间传递，以及残差连接在这一过程中的作用。

问题陈述

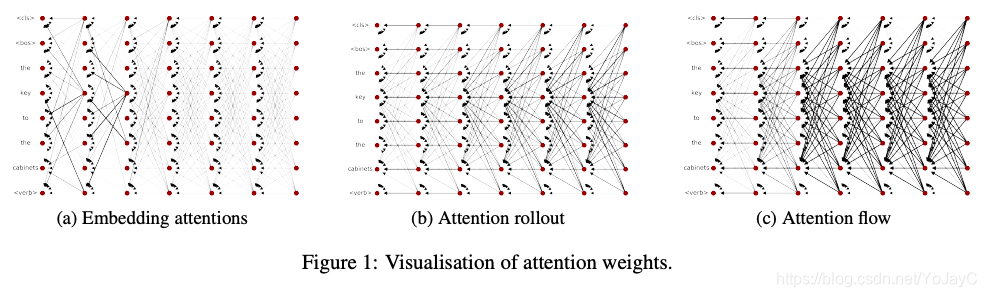
从图1a中的原始attention可以看出，只有在最开始的几层，不同位置的attention模式有一些区别，但是更高层中的attention权重更加一致。这表示随着模型层数的增加，嵌入的内容变得更加情境化，可能都带有类似的信息。此外，另一篇文章 $^{[1]}$ 中表示注意力权重不一定与输入token的相对重要性相对应。

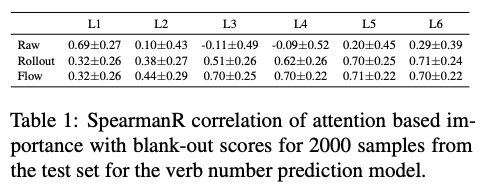
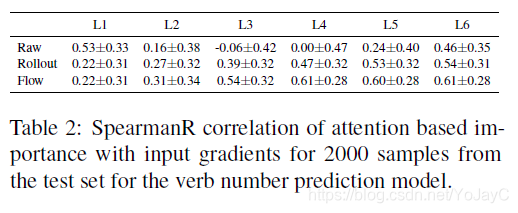
作者使用输入消融法，blank-out方法来估计每个输入token的重要性。Blank-out用UNK逐个替换输入中的每个token，衡量其对预测正确类别的影响程度。接着计算网络最后一层类别Embedding的attention权重和blank-out方法算出的重要性得分之间的Spearman秩相关系数，发现除了第一层之外，其他层的相关系数都很低，证实了前述文章中的观点。从表2可知，输入梯度和重要性得分之间的Spearman秩相关系数同样也很低。

Attention Rollout

给定一个模型和编码的Attention权重，Attention rollout递归计算每一层的token attetions。计算信息从输入层到更高层中的编码时，需要同时考虑模型的残差连接和attention权重，所以用额外表示残差连接的权重来增强attention graph。

给定一个具有残差链接的attention模块，将第 $l+1$ 层的attention值表示成 $V_{l+1}=V_{l}+W_{att}V_{l}$ ，其中 $W_{att}$ 是attention矩阵，因此有 $V_{l+1}=(W_{att}+I)V_{l}$ 。所以给attention矩阵增加一个单位矩阵来表示残差连接，然后重新归一化相加后的权重。计算的结果是 $A=0.5W_{att}+0.5I$ ，A表示用残差连接更新后的原始attention。

给定一个L层的Transformer，目标是计算从 $l_{i}$ 层所有位置到 $l_{j}$ 层所有位置的attention，其中 $j<i$ （反向计算）。在attention图中，从 $l_{i}$ 层位置k的结点v到 $l_{j}$ 层位置m的结点u有多个连接两个结点的边，如果将每一条边的权重视为两个结点间信息传递的一部分，那么可以将该路径中所有边的权重相乘来计算有多少信息从v传递到了u。因为attention图的两结点间可能不止一条边，所以为了计算从v到u传递的信息总量，对两结点间所有可能的路径求和。在实际计算时，为了计算从 $l_{i}$

到 $l_{j}$ 的attention，递归地将下面所有层的注意力权重矩阵相乘

$\tilde{A} = \left\{\begin{matrix} A(l_{i})\tilde{A}(l_{i-1}) & if i>j \\ A(l_{i}) & if i=j \end{matrix}\right.$

在上述等式中， $\tilde{A}$ 是Attention Rollout，A是原始的attention，乘法运算是矩阵乘法。在计算输入attention时，将j设置成0。

总之，Attention Rollout就是计算从底层到高层的Attention矩阵的乘积

References:

[1]. Sofia Serrano and Noah A. Smith. 2019. Is attention interpretable? In proceedings of the 57th Annual Meeting of the Association for Computational Linguistics. Association for Computational Linguistics