一、48. 旋转图像
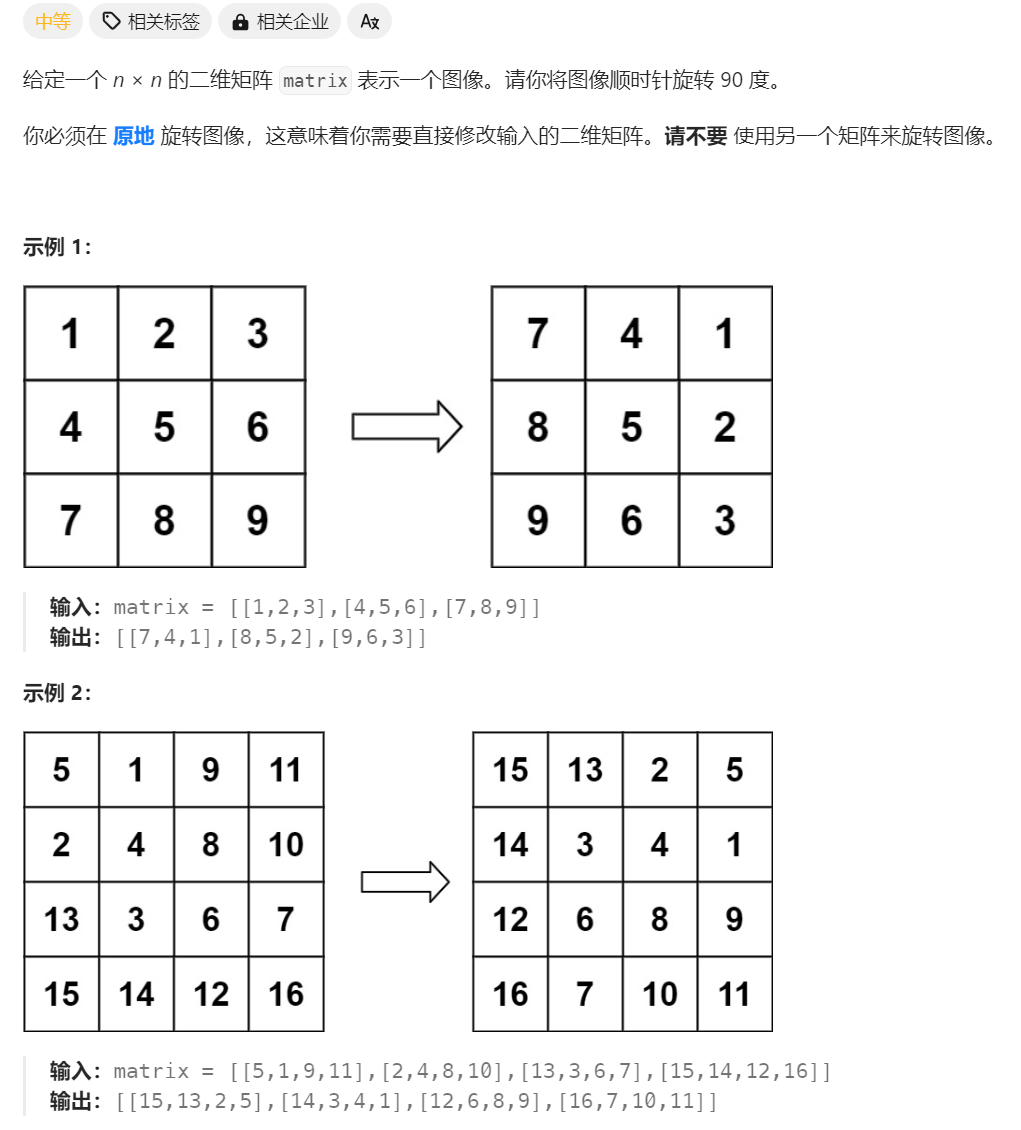
1.1:题目
1.2:解题思路
-
题型:顺/逆时针旋转矩阵;
-
❗❗核心思想/ 关键:不可暴力模拟,先镜像,后水平翻转
这题的意思很简单,就是让我们把矩阵顺时针选择90°,但是难点在于如何原地旋转。
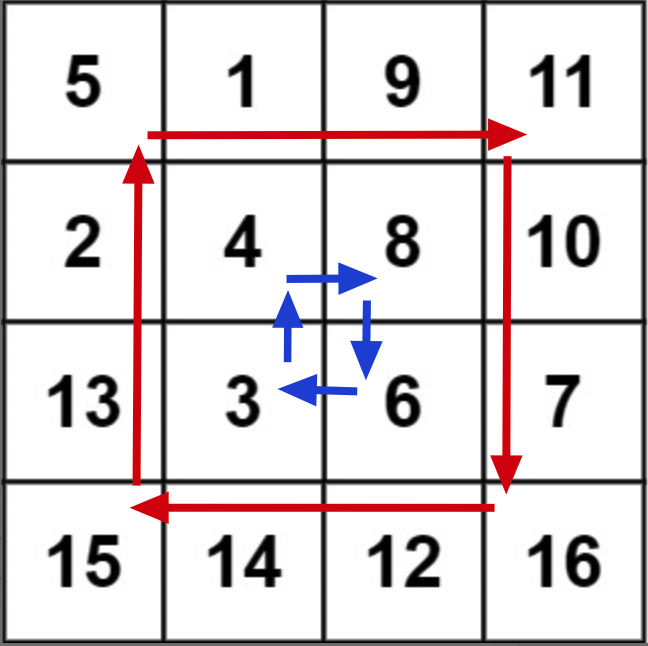
寻常的思路有以下两种:可能会误认为去模拟一下,一圈一圈的去遍历,然后进行旋转;又或者是想去找出当前坐标和旋转后像素对应坐标位置之间的关系,结果发现都想不出来很好的解决方法。这题的关键就在于不走寻常路。它用了另外一种比较巧妙的方法,对于计算机比较好理解,但对于我们可能一下子想不到的方法去解决了。(对于这种题,只要有个印象,以后遇到类似题目就不会懵圈了。
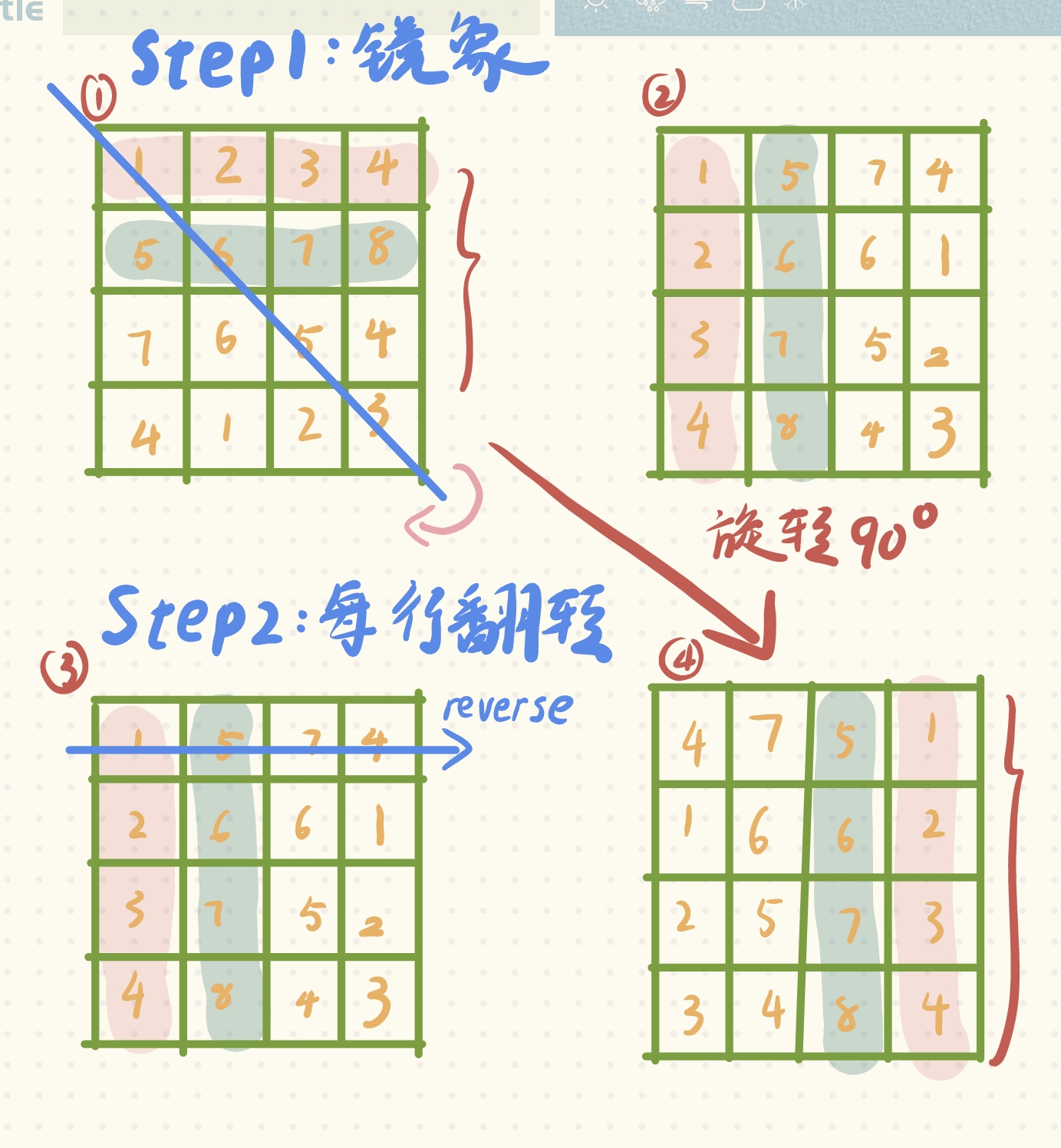
1.3:实现代码——c++
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
//Step1:先对原矩阵逐行遍历,进行镜像
for(int i = 0; i < matrix.size() - 1; i++){
for (int j = i + 1; j < matrix.size(); j++){
//对角线元素进行交换
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
//Step2: 每行进行翻转
for (int i = 0; i < matrix.size(); i++){
//对这一行元素进行翻转
for (int j = 0; j < matrix.size()/2; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[i][matrix.size() - j - 1];
matrix[i][matrix.size() - j - 1] = temp;
}
}
}
};
二、54. 螺旋矩阵
2.1:题目
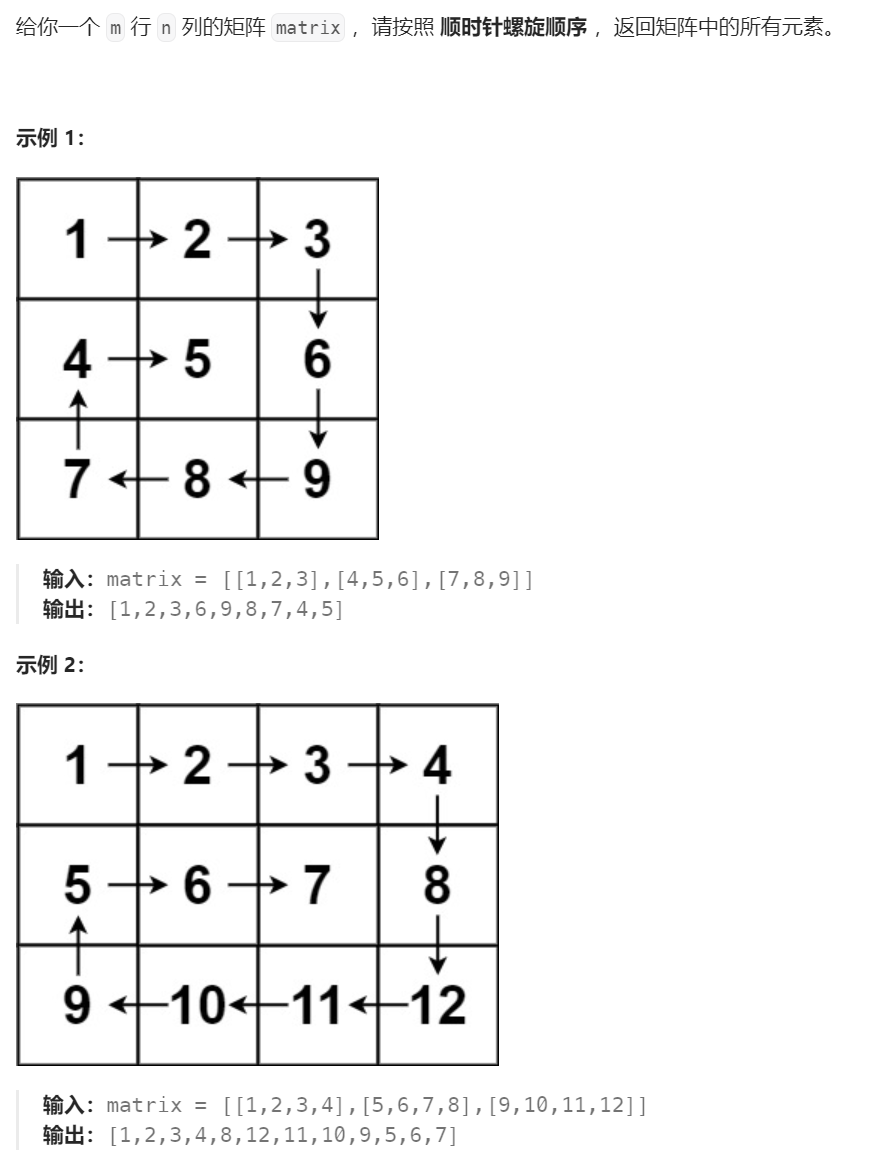
1.1:解题思路
- 题型:矩阵的螺旋遍历;
- ❗❗核心思想/ 关键:模拟,用四个边界点去控制遍历的边界!
这题最开始我的思路是先求出遍历几圈(一个圈数的大循环),然后根据边界和当前遍历圈数的关系再去一圈一圈的模拟遍历,发现真正这种纯模拟的方法,很不好把握边界,也很容易少加或者多加元素。
其实这题最好的思路如下图,设置四个边界标记变量,每一次循环完一圈后,更新一下四个边界。外面的大循环是结果数组的元素个数控制着(这样就不会多加或少加元素!)
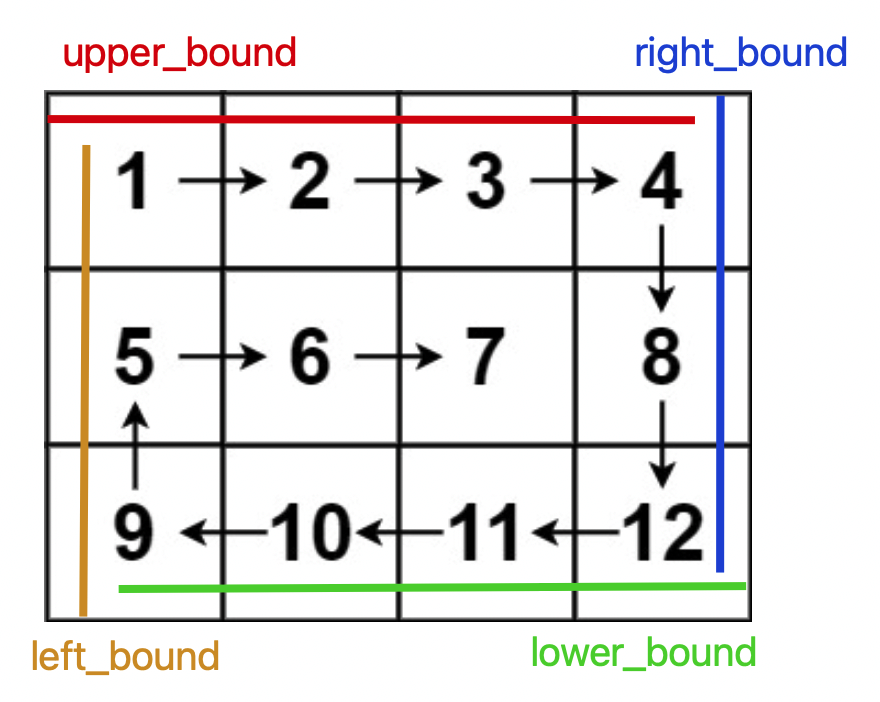
随着数组遍历,边界更新(收缩)
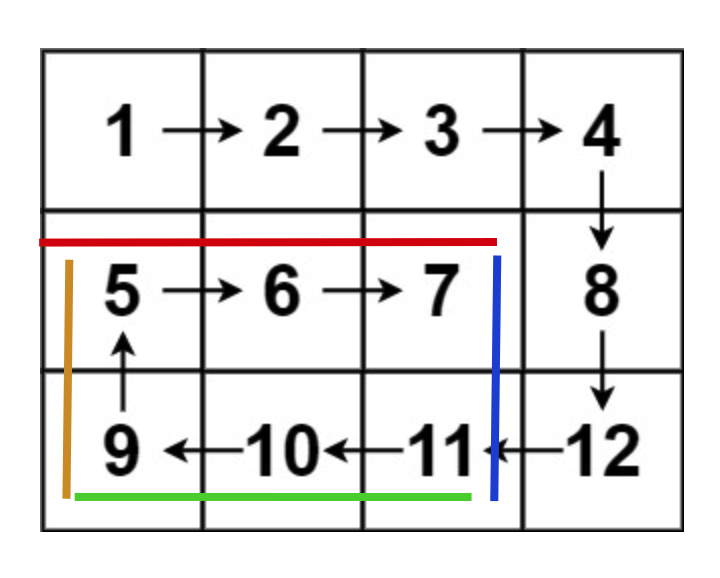
- 注意,在遍历完一条边后,边界点也要随之更新!!!
1.3:实现代码——c++
// 注意:cpp 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性,仅供参考。如有疑惑,可以参照我写的 java 代码对比查看。
#include <vector>
#include <deque>
using namespace std;
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
int upper_bound = 0, lower_bound = m - 1;
int left_bound = 0, right_bound = n - 1;
vector<int> res;
// res.size() == m * n 则遍历完整个数组
while (res.size() < m * n) {
if (upper_bound <= lower_bound) {
// 在顶部从左向右遍历
for (int j = left_bound; j <= right_bound; j++) {
res.push_back(matrix[upper_bound][j]);
}
// 上边界下移
upper_bound++;
}
if (left_bound <= right_bound) {
// 在右侧从上向下遍历
for (int i = upper_bound; i <= lower_bound; i++) {
res.push_back(matrix[i][right_bound]);
}
// 右边界左移
right_bound--;
}
if (upper_bound <= lower_bound) {
// 在底部从右向左遍历
for (int j = right_bound; j >= left_bound; j--) {
res.push_back(matrix[lower_bound][j]);
}
// 下边界上移
lower_bound--;
}
if (left_bound <= right_bound) {
// 在左侧从下向上遍历
for (int i = lower_bound; i >= upper_bound; i--) {
res.push_back(matrix[i][left_bound]);
}
// 左边界右移
left_bound++;
}
}
return res;
}
1.4:总结&易错点
- 在这题注意,四个边界点每遍历完一边就必须更新,因为边界点控制的遍历边界条件是左闭右闭!
- 每次遍历一条边之前,先判断一下是否满足遍历条件!!!(易错),否则容易重复遍历元素!!!
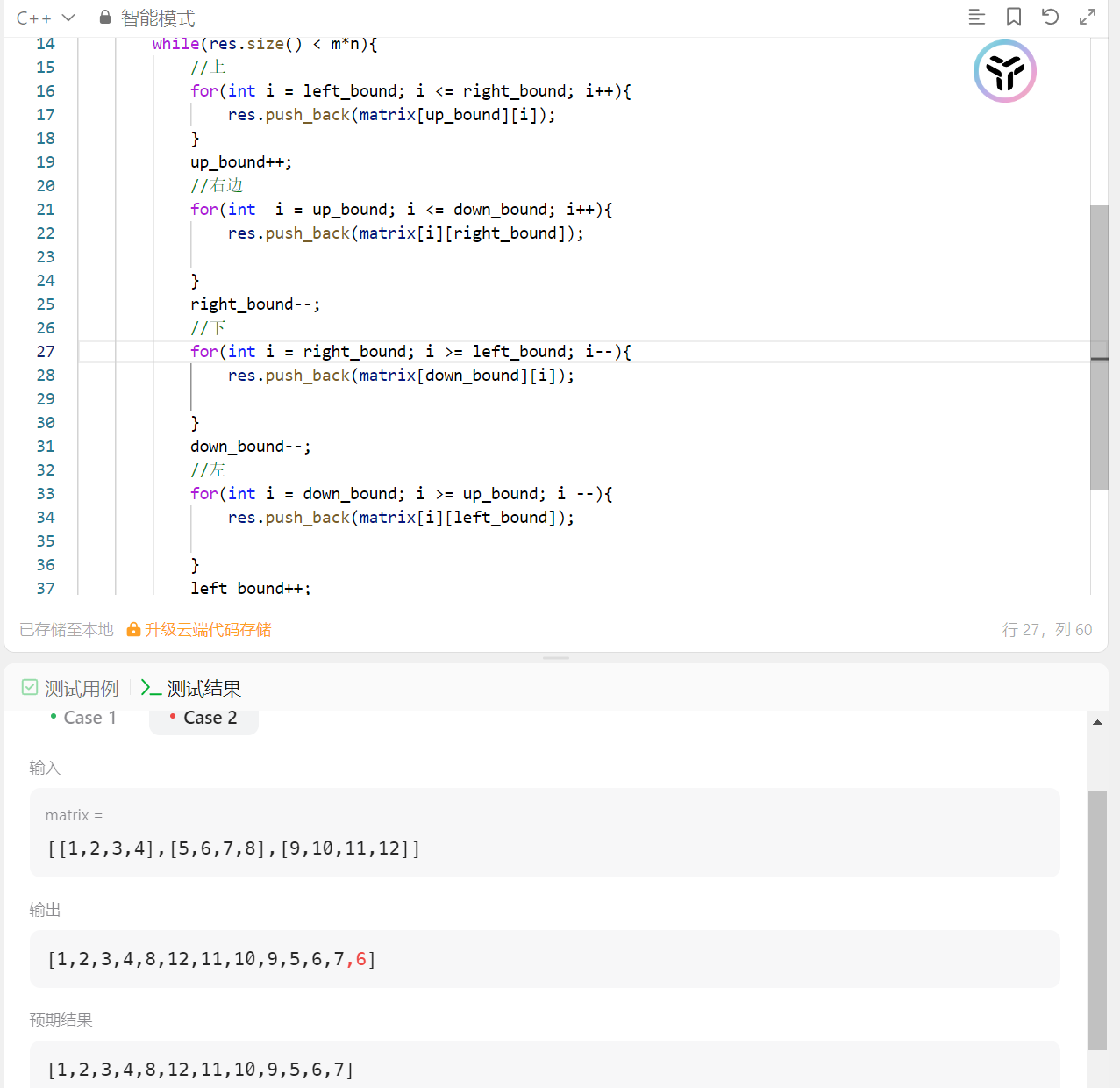
像下图这样,如果没有在遍历没条边之前进行if可行性判断,那么就会重复遍历元素!!!(在第二个循环的第三个if不能进去!!!因为遍历完上边之后,这一圈的元素都遍历完了)
为什么会出现这种情况呢?我们不是明明规定好边界了吗?因为每次在遍历一条边时,的确有边界,但是你要保证这个边界是合理的!!!如果边界合理,OK,你就可以遍历!!!但是在这题中,在边界缩小过程中,很有可能出现边界不合理的情况!!!





 文章讲述了如何使用C++解决旋转图像和螺旋矩阵问题,涉及核心思路如镜像、水平翻转以及利用边界点控制螺旋遍历。作者强调了不走寻常路的解题技巧和避免常见错误的方法。
文章讲述了如何使用C++解决旋转图像和螺旋矩阵问题,涉及核心思路如镜像、水平翻转以及利用边界点控制螺旋遍历。作者强调了不走寻常路的解题技巧和避免常见错误的方法。


















 372
372

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










