AcWing 788. 逆序对的数量（C++算法）

最新推荐文章于 2024-05-07 23:07:27 发布

原创

最新推荐文章于 2024-05-07 23:07:27 发布 · 476 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

本文介绍了一种高效计算逆序对数量的算法，通过使用归并排序的思想，在排序过程中统计逆序对数目，适用于大数据集，如AcWing788题。文章详细解析了算法步骤，并提供了C++实现代码。

AcWing 788. 逆序对的数量

1、题目（来源于AcWing）：
给定一个长度为n的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式
第一行包含整数n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式
输出一个整数，表示逆序对的个数。

数据范围
1≤n≤100000

输入样例：
6
2 3 4 5 6 1
输出样例：
5

2、基本思想：
假设一个函数merge_sort已经能求出逆序对的数量，若将这组数平分为左右两个部分，则：
逆序对的数量=左侧数内部逆序对的数量+右侧数内部逆序对的数量+右侧每个数与左侧数组成的逆序对数量的和
至于为什么要在找逆序对的时候排好序，是因为j之前比它大的数都找出来了，及时它比后面的大，但它被重新放到前面，它还是比后面的大，不影响。
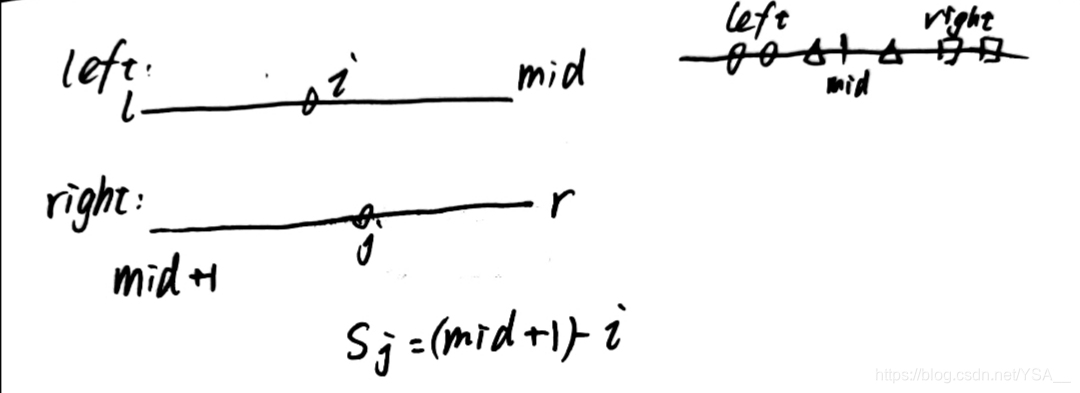
思想示意图
3、步骤：
①分为两组，将左右逆序对数量先加总
②归并的同时累加求同在左右两边的逆序对数量

4、C++代码如下（该代码引用AcWing网站的代码）：

#include <iostream>

using namespace std;

typedef long long ll;//long long比较长写起来比较麻烦，故用typedef

ll merge_sort(int l, int r);//该函数的功能为直接返回逆序对个数

const int N = 1e5 + 10;