寻找分类决策平面

1.超平面

在2维空间中的超平面是一条线，在3维空间中的超平面是一个平面。

2.平面的法向量

如果一非零向量垂直于一平面，这向量就叫做该平面的法向量。容易知道，平面上的任一向量均与该平面的法线向量垂直。

3.超平面的正反

一个超平面可以将它所在的空间分为两半, 它的法向量指向的那一半对应的一面是它的正面, 另一面则是它的反面。如果利用数学来判断的话，需要利用到法向量 w。

4.样本点到决策平面的距离

空间中任意一点$x_0$到超平面$S$的距离公式：$\frac{|w\cdot x_0+b|}{||w||}$.

推导过程：

取点空间中一点$x_0$,，超平面$S$：$w\cdot x+b=0$，其中$x_0,w,x$均为N维向量;

设点$x_0$到平面$S$的距离为$d$，点$x_0$在平面$S$上的投影点为$x_1$，则$x_1$满足$w\cdot x_1+b=0$;

因为向量$\overrightarrow{x_0{x}_1}$平行于$S$平面的法向量$w$，故有

$|w.\overrightarrow{x_0{x}_1}|=|w||\overrightarrow{x_0{x}_1}|=\sqrt[2]{w_1^2+w_2^2+...w_n^2}d=||w||d$

其中||w||为向量$w$的$L_2$范数；

又因,

$w\cdot \overrightarrow{x_0{x}_1}$

$=w^1(x_0^1-x_1^1)+w^2(x_0^2-x_1^2)+...+w^n(x_0^n-x_1^n)$

$=w^1{x}_0^1+w^2{x}_0^2+...+w^n{x}_0^n-(w^1{x}_1^1+w^2{x}_1^2+...+w^n{x}_1^n)$

$=w\cdot x_0+b$

故 $|w\cdot \overrightarrow{x_0{x}_1}|=|w\cdot x_0+b|=||w||d$

得,$d=\frac{|w\cdot x_0+b|}{||w||}$

5.二分类问题

对于二分类问题，假设有m个训练样本{(X(1),y(1))，(X(2),y(2))，...，(X(m),y(m))}\{ (X^{(1)},y^{(1)})， (X^{(2)},y^{(2)})，...， (X^{(m)},y^{(m)})\}{(X(1),y(1))，(X(2),y(2))，...，(X(m),y(m))}，其中，y∈{−1,1}y\in\{-1,1\}y∈{−1,1}。那么，应该如何从训练样本中得到分割超平面$w\cdot x+b=0$呢？

对于二分类问题，可以使用感知机模型来解决。其基本原理就是逐点修正，首先在超平面上随意取一条分类面，统计分类错误的点；然后随机对某个错误点就行修正，即变换直线的位置，使该错误点得以修正；接着再随机选择一个错误点进行纠正，分类面不断变化，直到所有的点都完全分类正确了，就得到了最佳的分类面。

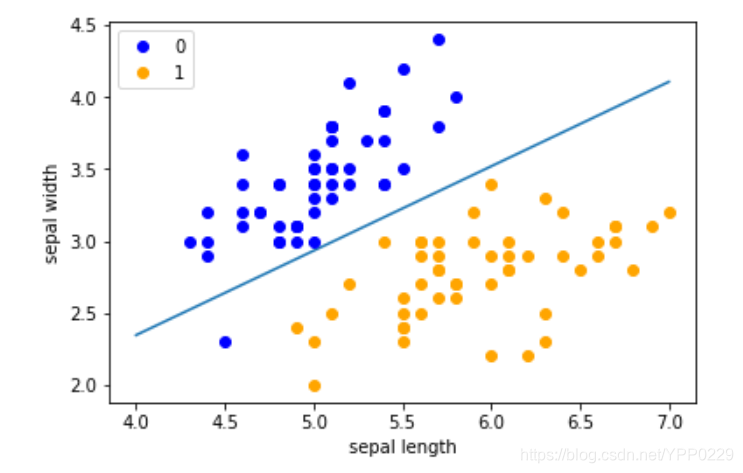
对上图的二分类问题，我们试图找到图中的分隔超平面，能够分割图中的正负样本，其中，分隔超平面为：
$$w\cdot x+b=0$$
如果我们有m个样本，每个样本对应于n维特征和一个二元类别输出，如下：
　$$(x_1^{(0)},x_2^{(0)},...x_n^{(0)},y_0),(x_1^{(1)},x_2^{(1)},...x_n^{(1)},y_1),...(x_1^{(m)},x_2^{(m)},...x_n^{(m)},y_m)$$
我们的目标是找到这样一个超平面，即：
$$w_0+w_1{x}_1+...+w_n{x}_n=0$$
为了简化这个超平面的写法，我们增加一个特征$x_0=1$，这样超平面为${\sum }_{i=0}^n{w}_i{x}_i=0$

寻找决策面的算法过程

输入：m个训练样本{(X(1),y(1))，(X(2),y(2))，...，(X(m),y(m))}\{ (X^{(1)},y^{(1)})， (X^{(2)},y^{(2)})，...， (X^{(m)},y^{(m)})\}{(X(1),y(1))，(X(2),y(2))，...，(X(m),y(m))}，其中y∈{−1,1}y\in\{-1,1\}y∈{−1,1}。

输出：$w，b$（即找到了分类的决策平面）

1. 赋初值：$w_0，b_0$
2. 从训练集中选取一个样本$（x_i，y_i）$
3. 判断该数据点是否为当前模型的误分类点，即判断 $y_i(w\cdot x_i+b)$的值，是大于0还是小于0，如果$y_i(w\cdot x_i+b)<0$则更新；
   $w=w+\eta y_i{x}_i$
   $b=b+\eta y_i$
4. 转到2，直到训练集中没有误分类点

利用余弦相似度进行分类，慢慢向点积靠拢

现在我们假设，有m个训练样本$(x_1^{(0)},x_2^{(0)},...x_n^{(0)},y_0),(x_1^{(1)},x_2^{(1)},...x_n^{(1)},y_1),...(x_1^{(m)},x_2^{(m)},...x_n^{(m)},y_m)$，$y_i$是第$i$个数据的分类标签，我们的训练样本可以分成两个类别，所以标签可以假定为$+$和$-$，其中每一类的样本个数为$n_{+}$和$n_{-}$。

正样本的中心点$C_{+}=\frac{1}{n_{+}}{\sum }_{y_i=+}{x}_i$，负样本的中心点$C_{-}=\frac{1}{n_{-}}{\sum }_{y_i=-}{x}_i$,

从$C_{+}$到$C_{-}$有一条差向量$w=C_{+}-C_{-}$，而$w$的中心点为$C$，所以在$C$点垂直于$w$的超平面就是两类的分类边界。

而想要把某个样本分为$+$的依据为，从$C$点到样本点的向量差与$w$向量的夹角应该小于90°，也即$0<cos\theta <1$；反之，$0>cos\theta >-1$。即，当内积为正，那就说明在分类1，内积为负，就说明在分类2。即：
$$y=sgn(<x_i-C，w>)$$