Clustering by fast search and find of density peaks——通过快速寻找和找到密度高峰进行聚类（笔记）

在进行学习这篇算法之前先复习以下知识

1. 什么是非监督学习
   在一个典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正
   样本和负样本的决策边界，在这里的监督学习中，我们有一系列标签，我们需要据此拟合一
   个假设函数。与此不同的是，在非监督学习中，我们的数据没有附带任何标签，我们拿到的
   数据就是这样的：

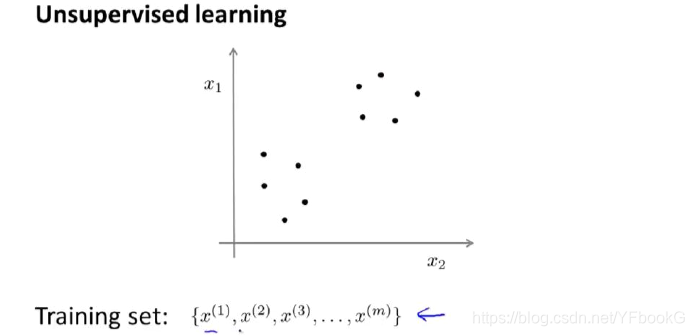
在这里我们有一系列点，却没有标签。因此，我们的训练集可以写成只有x(1),x(2)……一直到x(m)。我们没有任何标签y。因此，图上画的这些点没有标签信息。也就是说，在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。我们可能需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成两个分开的点集（称为簇），一个能够找到我圈出的这些点集的算法，就被称为聚类算法

以上出自吴恩达老师的机器学习课程

所谓非监督就是你的数据有任何的标签或者是有相同的标签或者就是没标签。所以我们已知数据集，却不知如何处理，也未告知每个数据点是什么。别的都不知道，就是一个数据集
非监督学习就是给出一个算法，让算法自行去筛选数据，在数据中找出某种结构

1. k-means聚类算法的思想是什么
   k均值算法是接受一个未标记的数据集，然后将数据聚类成不同的组（簇）
   K-均值是一个迭代算法，假设我们想要将数据聚类成n 个组，其方法为:
   （1）首先选择K 个随机的点μ1,μ2,…,μk，称为聚类中心（cluster centroids）；
   （2）对于数据集中的每一个数据，按照距离K 个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类（计算样本点与聚类中心的位置离哪个更近便划入哪个（是遍历整个样本点））。
   （3）计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置（把一个簇的均值点计算出来把聚类中心移到均值点）。
   依次重复迭代，直到聚类中心不再移动

用μ1,μ2,…,μk来表示聚类中心，用c(1),c(2),…,c(m)来存储与第i 个实例数据最近的聚类中心的索引，K-均值算法的伪代码如下：