量化相关内容（后续更新）

原创已于 2025-12-08 12:47:48 修改 · 99 阅读

CC 4.0 BY-SA版权

文章标签：

于 2025-12-07 22:10:26 首次发布

QuaRot

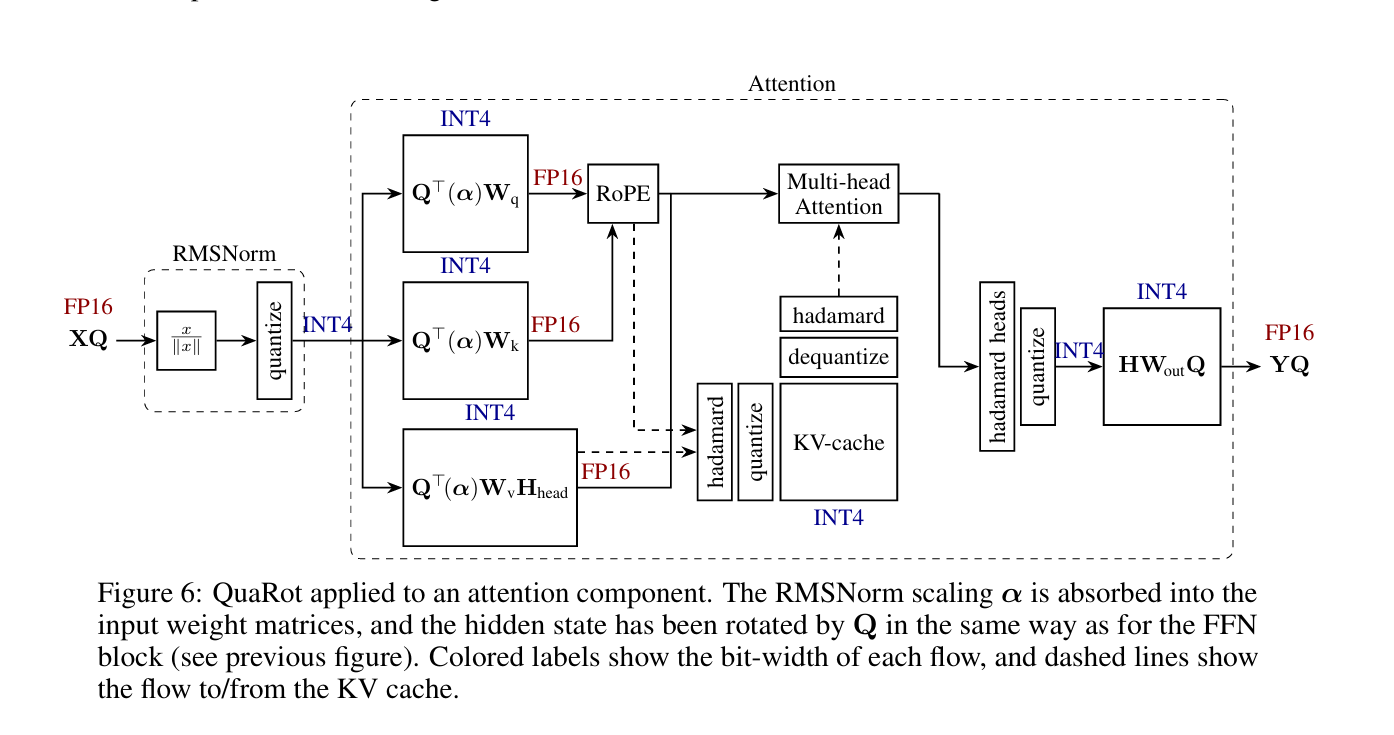
解释：

$Q$ ：随机hadamard矩阵

$\alpha$ ：RMSNorm的随机缩放因子

$quantize$ ：量化，缩放因子为每行最大值的绝对值除以7，每行值做除法舍入到最近整数 $IN4\epsilon \left ( -7,7 \right )$

$dequantize$ ：解量化

$RoPE$ ：进行位置编码，Q和K解量化为FP16输入

$Q^{T}(\alpha )$ ：抵消随机矩阵和进行缩放（离线）

$H_{head}$ ：用于 $V$ 值旋转，维度 $I_{nh}\times H_{dh}$ （离线）

$hadamard$ ：（在线）

写入 $KV-cache$ 时，对于 $K$ 实现旋转；对于 $Q$ 由于与 $K$ 相乘，用于消除变化影响；对于 $V$ 用于消除自身变化影响，以下定义为 $H_1$
读出 $KV-cache$ 时，消除解量化产生的异常，以下定义为 $H_2$
$H_1,H_2$ 与 $H$ 等价

$hadamard \ heads$ ：用于消除跨头异常值，维度 $H_{nh}\times I_{dh}$ （在线）

$HW_{out}$ ： $H$ 为全局hadamard矩阵，维度 $H_{nh}\times H_{dh}$ ，以下定义为 $H_h$

$Hadamard$ 正交且对称，由 $\left \{ -1,1 \right \}$ 组成， $H^TH=HH=I$

计算不变性：

正交变换：只改变向量的“分布形态”（打散异常值），不改变向量的内积/模长（保证注意力分数、加权结果不变）

异常值：“局部维度能量过高”—— 例如激活向量中某几个元素的绝对值远大于其他元素（如某元素为 100，其余仅为 1），这种 “不均衡” 被称为高非相干性

消除异常值：将高非相干性的异常值均匀分散到所有维度

假设激活向量x存在异常值（如x = [100, 1, 1, ..., 1]），其能量主要集中在第一个维度；
经过 Hadamard 变换(x' = Hx)后，由于正交变换的能量守恒，原第一个维度的 “100” 能量会被重新分配到所有维度（例如变为x' = [10, 11, 9, ..., 10]）；
变换后向量的最大元素从 100 降至 10 左右，与其他元素的差距显著缩小，非相干性大幅降低，异常值随之消除。
这种 “能量分散” 不改变向量的总范数，因此不会影响模型的最终输出 —— 这正是 “计算不变性定理” 的核心价值
总范数不变即 $\left \| Hx \right \|_2=\left \| x \right \|_2,\left \| Hx \right \|_2^2=\left ( Hx \right )^T\left ( Hx \right )=x^TH^THx=x^Tx=\left \| x \right \|_2^2$