决策树算法.实战.保存

简单记录下学习关于决策树的学习笔记
只有大体概念，不涉及细节

首先介绍熵的概念
熵用来表示数据混乱的程度
打比方：
熵高：比如义乌批发城，什么东西都有
熵低：比如苹果专卖店，只有苹果的产品

熵的计算公式

解释：如果pi（事件i发生的概率）越大，也就越接近1，取log之后，|logpi|也就越小了，而事件发生的可能性越低，pi就越接近0，取log之后 |logpi| 就越大， 0-1之间取log是负数，取负号变正数。 即H(X)越大说明这些事件发生的可能性都不大，就越混乱。

发生概率越接近0.5，熵值就越大
下图为熵的图像

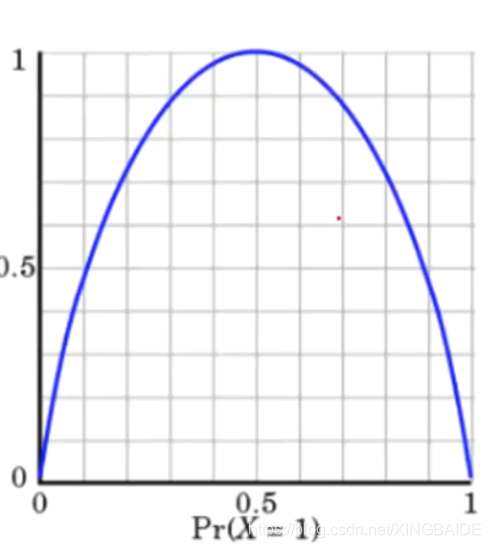
希望经过决策树的一次决策后，得到的集合熵越低

ID3算法：
信息增益：使得信息增益最大的那个作为当前的决策节点

熵值为0，也就是说一个集合里全都是同一类

ID3算法的不足：
如果有类似ID这样的属性，则必然导致大的信息增益，而成为根节点，不是想要的

C4.5:
信息增益率
信息增益/自身的熵值
比如ID属性，有14个id，则自身的熵值为 -log(1/14) 很大，信息增益率就很小

CART:使用GINI系数来当衡量标准

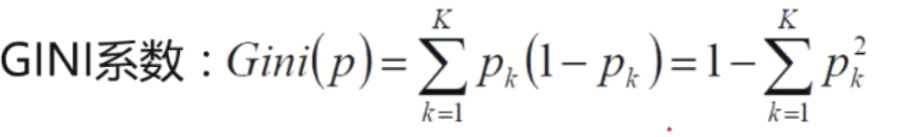
越肯定的事件，pk越接近1，则gini系数越接近0

剪枝：
决策树的过拟合风险大，对训练数据拟合得很好
预剪枝，和后剪枝
预剪枝：一边建树一边剪枝，控制输入数的深度，控制深度和宽度
后剪枝：先建树，回头剪枝
普遍使用预剪枝

预剪枝：

1. 限制深度为n，则深度n之下的树就不要了
2. 限制叶子节点的个数，叶子节点达到要求时则不再分裂
3. 限制叶子样本数，每个叶子节点内都有若干个样本，比方说设置为10，则某个叶子节点个数为8的话，就不再分裂了
4. 信息增益，分裂时信息增益小于某个阈值则不分裂

后剪枝：

C(t)为某个叶子节点的gini系数乘该叶子节点的样本数，Tleaf为叶子节点数目

实战可以参考;
https://www.cnblogs.com/pinard/p/6056319.html
https://blog.youkuaiyun.com/qq_28409193/article/details/80112746

神tm…找了半天都只有决策树保存的方法,没有读取的办法…
sklearn中存树：

fw = open("./output/RegressorTree", 'wb')
    pickle.dump(treelist[loc], fw)
    fw.close()

读树：

fr = open("./output/RegressorTree", 'rb')
    mytree= pickle.load(fr)