B树的插入

链接：https://blog.youkuaiyun.com/baidu_37964071/article/details/79533027
一、B树的定义
1970年，R. Bayer和E.m ccreight 提出了一种适合外查找的树，它是一种平衡的多叉树，称为B树，有些地方写的是B-树，注意不要误读成"B减树"）
1、B树（B-tree）是对2-3树数据结构的扩展，又称为多路平衡查找树，它的一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同
2、B树是一种自平衡树数据结构，可以保持数据排序，它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构
3、B树针对读写大数据块的系统进行了优化。B树的算法减少定位记录时所经历的中间过程，从而加快存取速度。普遍运用在数据库和文件系统。

二、B树的性质
一棵M阶(M>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足一下性质：

1. 根节点至少有两个孩子
2. 每个非根节点至少有M/2(上取整)个孩子,至多有M 个孩子 3. 每个非根节点至少有M/2-1( 上取整)个关键字,至多有M-1个关键字，并且以升序排列
3. key[i]和key[i+1]之间的孩子节点的值介于key[i ]、key[i+ 1]之间
4. 所有的叶子节点都在同一层
   三、B树的插入
   步骤：
   1、插入一个元素时，首先在B树中是否存在，如果不存在，即比较大小寻找插入位置，在叶子结点处结束，然后在叶子结点中插入该新的元素
   2、如果叶子结点空间足够，这里需要向右移动该叶子结点中大于新插入关键字的元素，如果空间满了以致没有足够的空间去添加新的元素，则将该结点进行“分裂”，将一半数量的关键字元素分裂到新的其相邻右结点中，中间关键字元素上移到父结点中（当然，如果父结点空间满了，也同样需要“分裂”操作）
   3、当结点中关键元素向右移动了，相关的指针也需要向右移。如果在根结点插入新元素，空间满了，则进行分裂操作，这样原来的根结点中的中间关键字元素向上移动到新的根结点中，因此导致树的高度增加一层

eg：M阶B树–M=3
{53 , 75 , 139 , 49, 145, 36, 101};

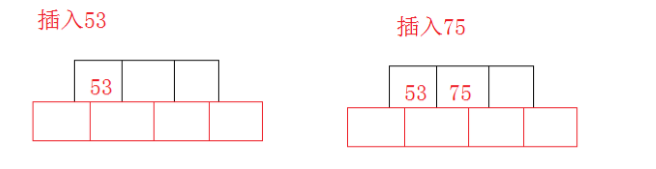
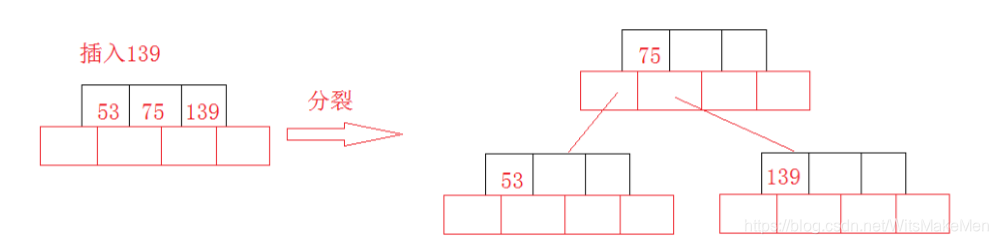
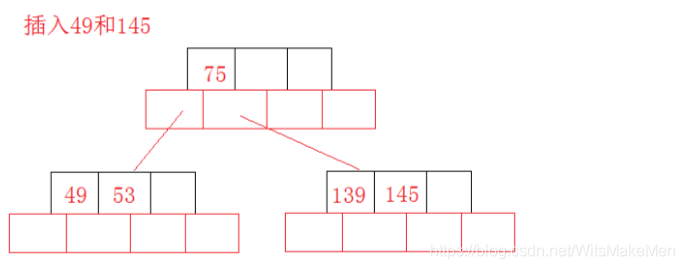
插入36：

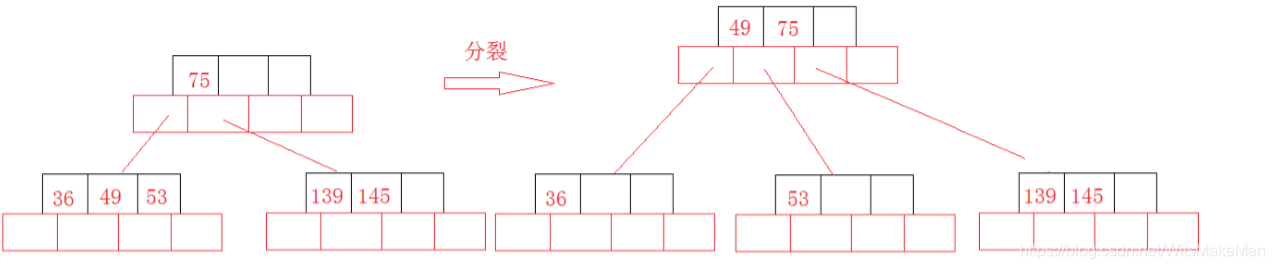
插入101后还需要分裂。

代码：
#include
using namespace std;

template<class K,int M=3>
struct BTreeNode
{
BTreeNode()
:_pParent(NULL)
, _size(0)
{
for (size_t i = 0; i <= M; i++)
{
_pSub[i] = NULL;
}
}

K _key[M];
BTreeNode<K, M> *_pSub[M + 1];
BTreeNode<K, M> *_pParent;
size_t _size;

};

template<class K,int M=3>
class BTree
{
typedef BTreeNode<K, M> Node;
typedef Node* pNode;
public:
BTree()
:_pRoot(NULL)
{}

bool Insert(K& key)
{
	if (_pRoot == NULL)     //无根节点
	{
		_pRoot = new Node();
		_pRoot->_key[0] = key;
		_pRoot->_size = 1;
		return true;
	}

	pair<pNode, int> ret = Find(key);
	if (ret.second >= 0)
		return false;
	pNode pCur = ret.first;
	pNode pSub = NULL;
	while (1)
	{
		_Insert(pCur, key, pSub);
		size_t size = pCur->_size;
		if (size < M)
			return true;
		else
		{
			size_t mid = size >> 1;
			pNode tmp = new Node();
			for (size_t i= mid + 1; i < size; i++)
			{
				tmp->_key[tmp->_size] = pCur->_key[i];
				tmp->_pSub[tmp->_size] = pCur->_pSub[i];
				if (tmp->_pSub[tmp->_size])
					tmp->_pSub[tmp->_size]->_pParent = tmp;
				tmp->_size++;
			}
			tmp->_pSub[tmp->_size] = pCur->_pSub[pCur->_size];

			if (tmp->_pSub[tmp->_size])
				tmp->_pSub[tmp->_size]->_pParent = tmp;
			pCur->_size -= (tmp->_size + 1);               //处理size

			if (pCur == _pRoot)                            //如果当前结点是根结点，还需要再处理
			{
				_pRoot = new Node;
				_pRoot->_key[0] = pCur->_key[mid];
				_pRoot->_pSub[0] = pCur;
				pCur->_pParent = _pRoot;
				_pRoot->_pSub[1] = tmp;
				tmp->_pParent = _pRoot;
				_pRoot->_size = 1;
				return true;
			}
			else
			{
				key = pCur->_key[mid];
				pCur = pCur->_pParent;
				pSub = tmp;
			}
		}
	}
}

pair<pNode, int> Find(const K& key)
{
	pNode pCur = _pRoot;
	pNode pParent = NULL;

	while (pCur)
	{
		size_t i = 0;
		while (i < pCur->_size)
		{
			if (key == pCur->_key[i])
				return pair<pNode, int>(pCur, i);
			else if (key < pCur->_key[i])
				break;
			else
				i++;
		}
		pParent = pCur;
		pCur = pCur->_pSub[i];
	}
	return make_pair(pParent, -1);//没找到返回-1
}

private:
void _Insert(pNode pCur, const K& key, pNode pSub)
{
//直接插入的思想
int end = pCur->_size - 1;
while (key < pCur->_key[end] && end >= 0)
{
pCur->_key[end + 1] = pCur->_key[end];
pCur->_pSub[end + 2] = pCur->_pSub[end + 1];
end–;
}

	pCur->_key[end + 1] = key;
	pCur->_pSub[end + 2] = pSub;
	if (pSub)
		pSub->_pParent = pCur;
	pCur->_size += 1;
}

private:
Node *_pRoot;
};

int main()
{
int arr[] = { 53, 75, 139, 49, 145, 36, 101 };
BTree b;
size_t size = sizeof(arr) / sizeof(arr[0]);
for (size_t i = 0; i < 7; i++)
b.Insert(arr[i]);

system("pause");
return 0;

}