读《微波工程(第三版)》笔记 (3：介质中的边界条件)

原创

已于 2022-10-11 20:05:32 修改 · 3.9k 阅读

·

3

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

于 2022-10-11 11:42:46 首次发布

本文探讨了在特定边界条件下，如何求解麦克斯韦方程组以获取电位移矢量、磁感应强度等物理量的具体表达式。通过分析不同介质间的分界面，详细阐述了法向和切向场的连续性和不连续性的数学描述。

求解微分形式的麦克斯韦方程组(详见笔记1) ，必须已知边界上的值时，才能有完整切唯一的解。

常用的方法是：在一定的区域求解无源麦克斯韦方程组获得带有未知系数的通解，再利用边界条件来求得这些系数

我的理解：麦克斯韦方程组+边界条件=特解

目录

一般材料分界面上的场

电位移矢量

磁感应强度

介质分界面的场

理想导体（电壁）分界面的场

磁壁边界条件

一般材料分界面上的场

分析模型

考虑两种媒质之间的平面界面，如图3.1所示：

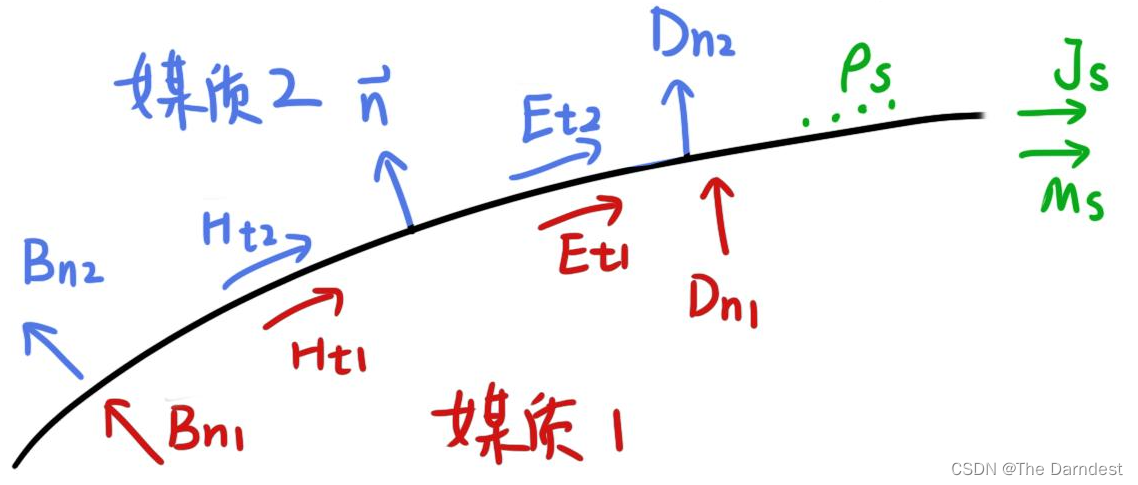
图 3.1

其中，两个介质内的场和分界面上的场都用颜色进行了区分。

利用积分形式的麦克斯韦方程组来推导分界面上的的法向、切向场的边界条件。

我们可以选取如图3.2所示的闭合高斯曲面作为分析工具，主要用来分析电位移矢量和磁感应强度。它是一个圆柱面，上下底面横跨两种媒质，并且要求高度h->0。

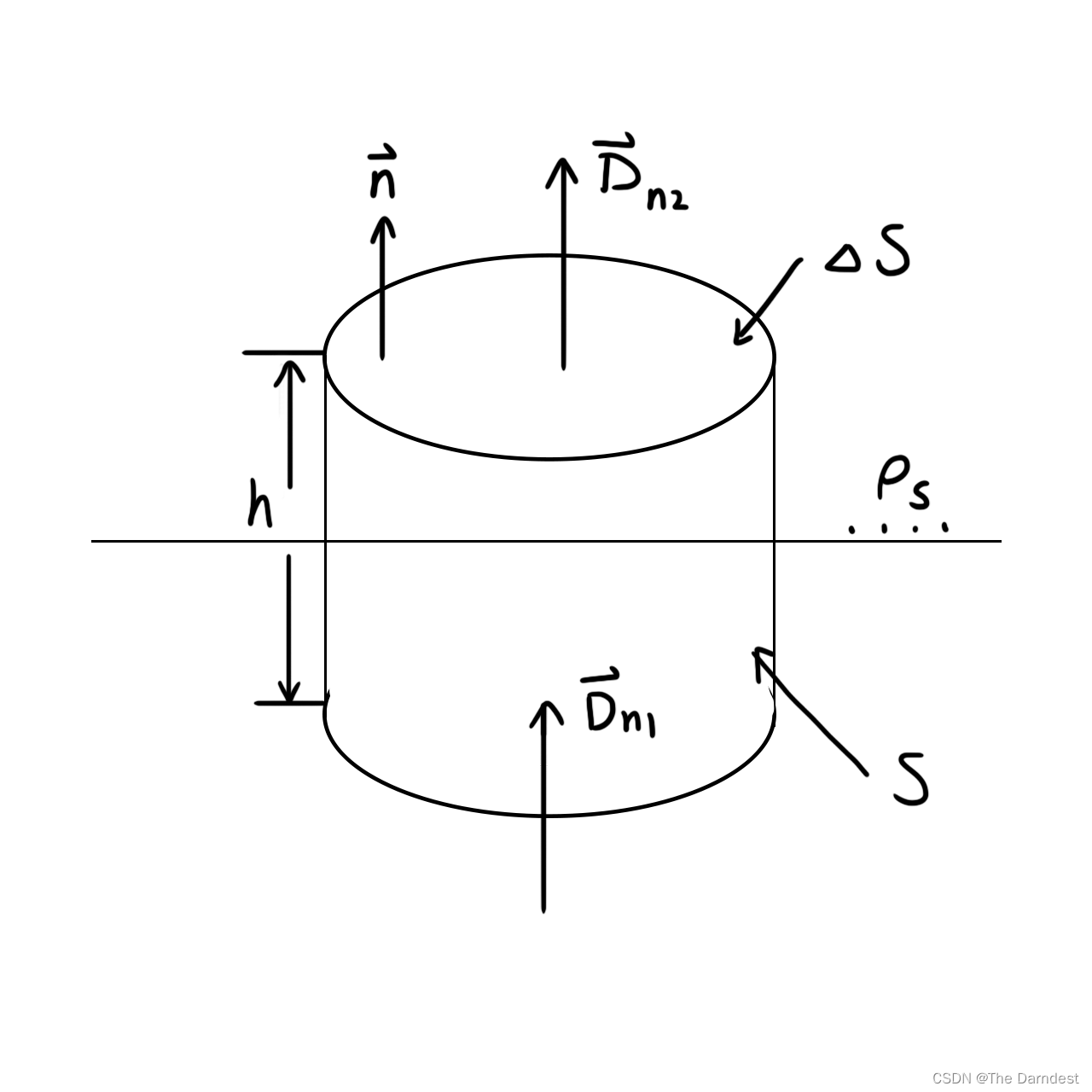
图 3.2

分析磁场、电场时，可以使用图3.3

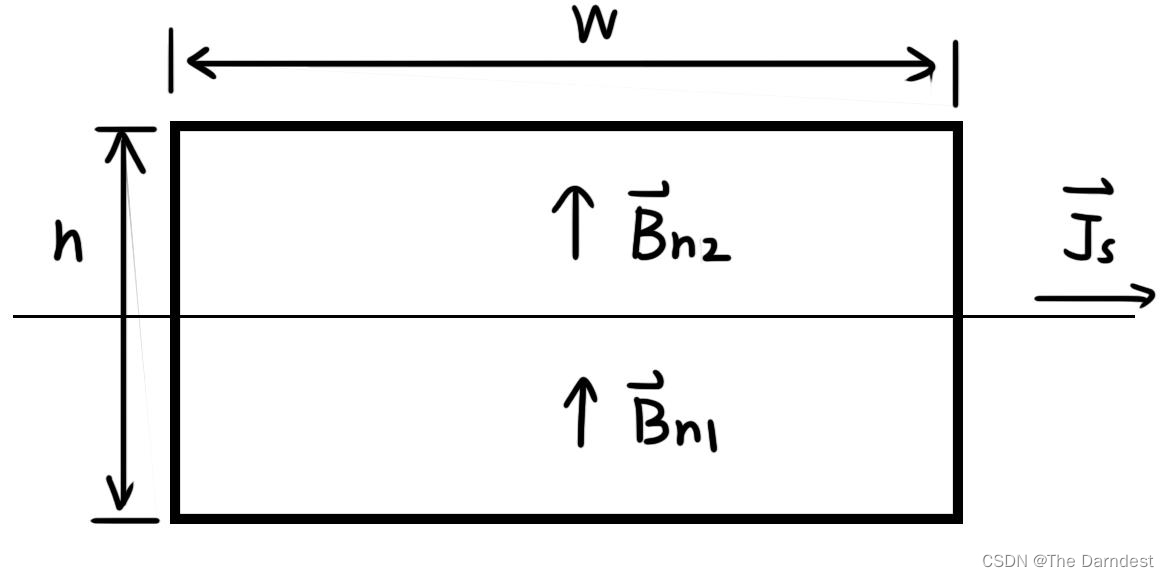
图 3.3（这里有点小错误，别管两个磁感应强度）

电位移矢量

电位移矢量满足高斯定理：

$\oint _{S}\overrightarrow{D}\cdot d\overrightarrow{s}=\int _{V}\rho d\nu=Q$

由于高度h趋于0，此时圆柱侧面的电位移通量贡献为0，可以简化为：

$\begin{} {\color{black} \Delta S\cdot D_{n2} - \Delta S\cdot D_{n1} = \Delta S\cdot \rho_{s}} \\\\ D_{n2}-D_{n1}=\rho_{s} \end{}$

如果写成矢量形式，则为：

$\widehat{n}\cdot (\overrightarrow{D_{2}}-\overrightarrow{D_{1}})=\rho_{s}$

也就是：电位移矢量在边界上法向不连续，数值相差为分界面上的面电荷密度。

磁感应强度

同样地，将磁通连续性方程的积分形式

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。