常用激活函数

可见，激活函数能够帮助我们引入非线性因素，使得神经网络能够更好地解决更加复杂的问题。

1. Sigmoid

$sigmoid(x)=\frac{1}{1+e^{-x}}$

$sigmoi{d}^{\prime }(x)=\frac{1}{1+e^{-x}}$

Sigmoid 函数的取值范围在 (0,1) 之间，单调连续，求导容易，一般用于二分类神经网络的输出层。

函数图像和导数图像：

import math
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10,10)
a=np.array(x)
y1=1/(1+math.e**(-x)) # 函数值
y2=math.e**(-x)/((1+math.e**(-x))**2) # 导数值
plt.xlim(-11,11)
ax = plt.gca() # get current axis 获得坐标轴对象
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none') # 将右边 上边的两条边颜色设置为空 其实就相当于抹掉这两条边
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left') # 指定下边的边作为 x 轴   指定左边的边为 y 轴
ax.spines['bottom'].set_position(('data', 0)) #指定 data  设置的bottom(也就是指定的x轴)绑定到y轴的0这个点上
ax.spines['left'].set_position(('data', 0))
plt.plot(x,y1,label='Sigmoid',linestyle="-", color="blue") #label为标签
plt.plot(x,y2,label='Deriv.Sigmoid',linestyle="--", color="red") #l
plt.legend(['Sigmoid','Deriv.Sigmoid'])

优缺点

优点：
sigmoid 是使用范围最广的一类激活函数，具有指数函数形状，它在物理意义上最为接近生物神经元。此外，(0, 1) 的输出还可以被表示作概率，或用于输入的归一化，代表性的如Sigmoid交叉熵损失函数。

缺点：
（1）首先，Sigmoid 函数软饱和区范围广（左右趋向于无穷的两个部分），容易造成梯度消失，使得网络参数很难得到有效训练。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象
（2）此外，sigmoid函数的输出均大于0，使得输出不是0均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。这样会使权重更新效率降低。
（3）最后还有一点，Sigmoid 函数包含 exp 指数运算，运算成本也比较大。

注：软饱和：$li{m}_{x\to \infty }{f}^{\prime }(x)=0$

2. Tanh

$tanh(x)=\frac{sinhx}{coshx}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

$tan{h}^{\prime }(x)=1-tan{h}^2(x)$

函数图像和导数图像：

优缺点：
优点：
与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid快，减少迭代次数。

缺点：
tanh一样具有软饱和性，从而造成梯度消失，在两边一样有趋近于０的情况

3. ReLU

ReLU的全称是Rectified Linear Units，是一种AlexNet时期才出现的激活函数。

$$relu(x)=max(0,x)=\{\begin{array}{ll}0& x<0\\ x& x>0\end{array}$$

$$rel{u}^{\prime }(x)=\{\begin{array}{ll}0& x<0\\ 1& x>0\end{array}$$

函数图像和导数图像：

优缺点
优点：
（1）在SGD（随机梯度下降算法）中收敛速度够快，大约是 sigmoid/tanh 的 6 倍。。
（2）可以看到，当x<0时，ReLU硬饱和，而当x>0时，则不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。这让我们能够直接以监督的方式训练深度神经网络，而无需依赖无监督的逐层预训练。
（3）没有复杂的指数运算，计算简单、效率提高。

缺点：
（1）与Sigmoid类似，ReLU的输出均值也大于0，偏移现象和神经元死亡会共同影响网络的收敛性。
（2）前向传导（forward pass）过程中，如果 x < 0，则神经元保持非激活状态，且在后向传导（backward pass）中「杀死」梯度。这样权重无法得到更新，网络无法学习。神经元死亡是不可逆的。

注：硬饱和：$f\prime (x)=0$

4. Leaky ReLU & PReLU

为了改善ReLU在x<0时梯度为0造成Dead ReLU，提出了Leaky ReLU使得这一问题得到了缓解。例如在我们耳熟能详的YOLOV3网络中就使用了Leaky ReLU这一激活函数，一般$\alpha$取0.25。

另外PReLU就是将Leaky ReLU公式里面的当成可学习参数参与到网络训练中。

$$leaky-relu(x)=\{\begin{array}{ll}\alpha x& x<0,(0<\alpha <1)\\ x& x>0\end{array}$$

$$leaky-rel{u}^{\prime }(x)=\{\begin{array}{ll}\alpha & x<0,(0<\alpha <1)\\ 1& x>0\end{array}$$

函数图像：

Leaky ReLU 的优点与 ReLU 类似：

• 没有饱和区，不存在梯度消失问题。
• 没有复杂的指数运算，计算简单、效率提高。
• 实际收敛速度较快，大约是 Sigmoid/tanh 的 6 倍。
• 不会造成神经元失效，形成了“死神经元”。

5. ELU

$$elu(x)=\{\begin{array}{ll}\alpha (e^x-1)& x<0,(0<\alpha <1)\\ x& x>0\end{array}$$

函数图像：

ELU 融合了sigmoid和ReLU，左侧具有软饱和性，右侧无饱和性。右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱能够让ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于零，所以收敛速度更快。

• 没有饱和区，不存在梯度消失问题。
• 没有复杂的指数运算，计算简单、效率提高。
• 实际收敛速度较快，大约是 Sigmoid/tanh 的 6 倍。
• 不会造成神经元失效，形成了“死神经元”。
• 输出均值为零
• 负饱和区的存在使得 ELU 比 Leaky ReLU 更加健壮，抗噪声能力更强。

但是，ELU 包含了指数运算，存在运算量较大的问题。

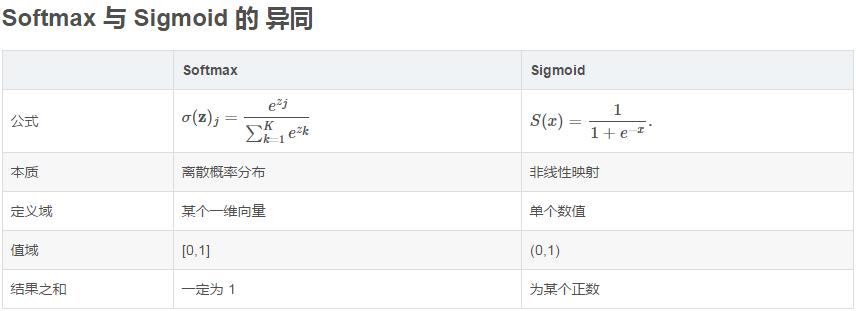
6. Softmax

Softmax - 用于多分类神经网络输出。

假设有n个元素，第i个元素的Softmax输出值为：

$$Softma{x}_i(x)=\frac{e^x}{{\sum }_{i=1}^n{e}^i}$$