2024年小美赛B题Heesch数

是Winky啊

已于 2024-12-05 10:34:16 修改

阅读量899

点赞数 29

分类专栏：竞赛文章标签：数学建模

于 2024-11-30 21:34:22 首次发布

本文链接：https://blog.youkuaiyun.com/Winkyyyyyy/article/details/144133946

版权

竞赛专栏收录该内容

2 篇文章

订阅专栏

2024 年认证机构杯国际数学建模竞赛

http://mcm.tzmcm.cn

1. 问题分析

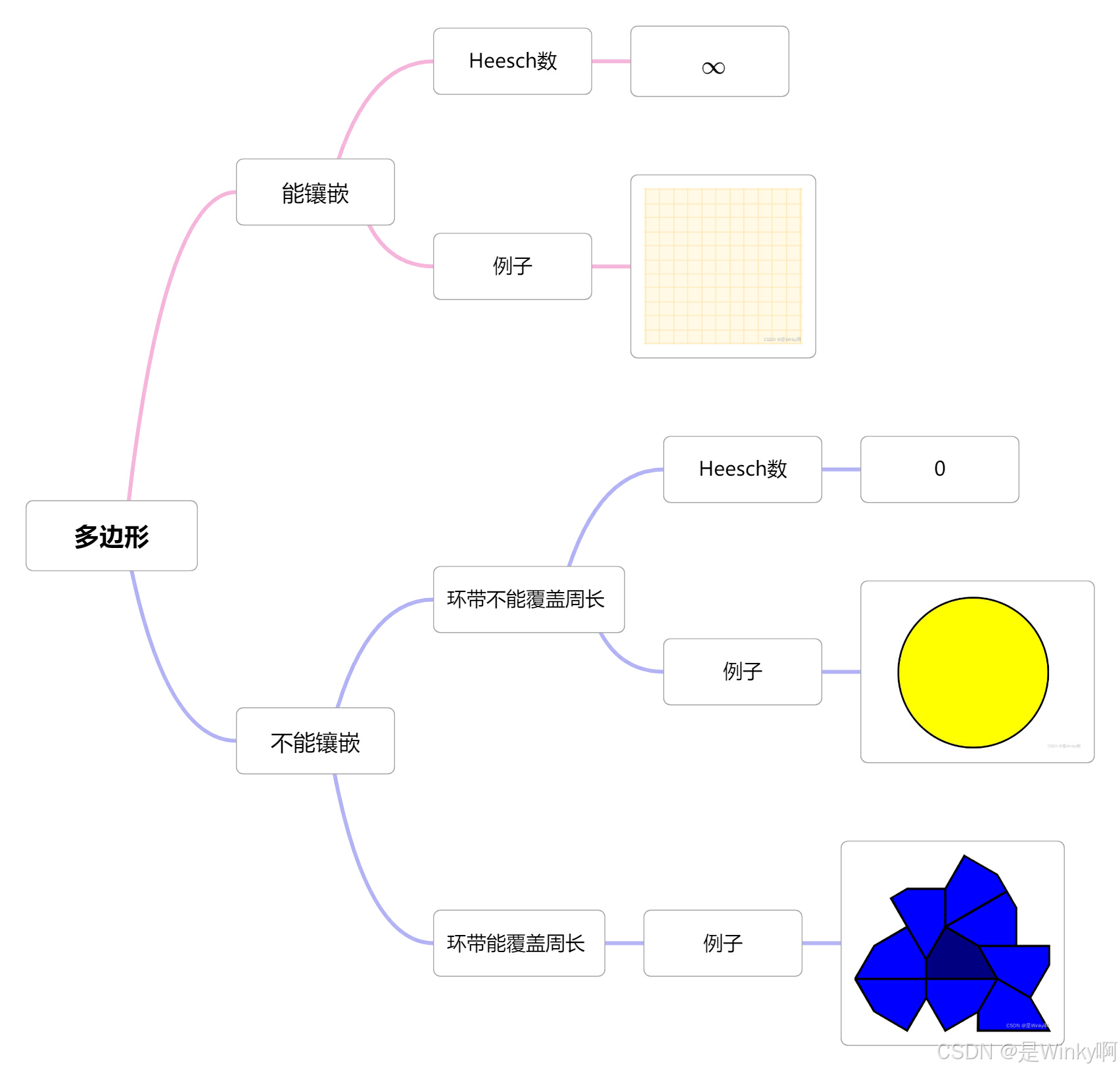
🧀多边形分类

🧀Heesch数定义

Heesch 的问题 - 维基百科，自由的百科全书 --- Heesch's problem - Wikipedia

在几何图形中，形状的 Heesch 数是同一形状的副本的最大层数，该副本可以围绕它，没有重叠和间隙。

🧀环带

环带是指对于一个多边形，当用与它相同的多边形通过旋转、平移和镜像等操作围绕其形成一圈没有缝隙的多边形组合时，这一圈多边形组合被称为该多边形的环带。

第 $0$ 环带是多边形本身

$k> 0$ 时，第 $k$ 个环带是与第 $\left ( k-1 \right )$ 个环带共享边界点的瓷砖集合

图形 $S$ 的黑施数是存在特定条件下 $k$ 的最大值

目前已知的有限的最大黑施数是 $6$

Heesch Number 6 的人物：突破二十年的界限 |数学智能者

🧀例子

Heesch数	图像
0
1
1
2
4
5
6
$\infty$

2. Heesch数

构建数学模型和算法创建具有最大黑施数的多边形，描述算法原理、实现过程和最终结果，不一定要超已知最佳结果，但算法自动生成最大可能结果即可。

这道题讨论的Heesch数是有限且非0的，要求解的多边形是不能镶嵌且环带能覆盖周长的。

符合要求的多边形有两种，一种是直线型图形，一种是曲线型图形。

🧀直线型图形

🍕随机

🍔生成原始图形 $S_{0}$

生成有 $n$ 个随机顶点的多边形 $S_0=\{(\theta _i,r_i)\mid i=1,2,\cdots,m\}$

其中 $0\leq \theta_{i}\leq 2\pi$ ， $0\leq r_{i}\leq 100$

🍔假设

$S_0=\{(\theta _i,r_i)\mid i=1,2,\cdots,m\}$ 为多边形本身

$S_{1}=\left \{S_{11}\cup S_{12}\cup \cdots\cup S_{1j}|j=1,2, \cdots,n_1\right \}$ 为环带 $1$ ；

$S_{2}=\left \{S_{21}\cup S_{22}\cup \cdots\cup S_{2j}|j=1,2, \cdots,n_2\right \}$ 为环带 $2$ ；

$S_{k}=\left \{S_{k1}\cup S_{k2}\cup \cdots\cup S_{kj}|j=1,2, \cdots,n_k\right \}$ 为环带 $k$ 。

$k$ 为该多边形对应的最大环带数，即Heesch数。

🍔约束条件

$S_{0}=S_{1j}=\cdots =S_{kj}$ ， $S_{k1}=S_{k2}=\cdots =S_{kj}$

$S_{0}\cap S_{1}\cap...\cap S_{k-1}\cap S_{k}=0$ ， $S_{k1}\cap S_{k2}\cap...\cap S_{k(j-1)}\cap S_{kj}=0$

$S_{0}\cup S_{1}\cup...\cup S_{k-1}\cup S_{k}$ 是一个单连通多边形，

$S_k$ 包围 $S_{ k-1 }$

🍔生成环带 $S_{k}$

🍔最优化

如何排列环带使 $k$ 最大

这种方法生成的多边形十分随机，生成的多边形符合要求的可能性极小。

🍕由正三角形组成

A Figure with Heesch Number 6: Pushing a Two-Decade-Old Boundary | The Mathematical Intelligencer

🍔生成原始图形 $S_{0}$

生成原始图形这里有两种方案。

边扩展法

先生成一个等边三角形，为初代图形，将等边三角形的三个边存入边的集合。

我们在这里随机选择一条边，在这条边的基础上生成一个不与原图形重叠的正三角形。

将新加的三角形的边加入边的集合，刚刚选择的边变为图形内部的一部分，从中边集中删除。

……

这里注意，我们要先设置好组成原始图形的三角形个数。

中心点扩展法

构造二维直角坐标系，将每一个三角形用中心点表示，设三角形的边长为 $l$ 。

设初代图形是顶点朝上的正三角形，用它的中心点 $\left(\frac l2,\frac l{2\sqrt{3}}\right)$ 表示。

对于顶点朝上的三角形，若要“扩展”，则有三种情况 $\left(x-\frac{\ell}{2},y+\frac{l}{2\sqrt{3}}\right)$ , $\left(x+\frac{\ell}{2},y+\frac{l}{2\sqrt{3}}\right)$ , $\left(x,y-\frac{l}{\sqrt{3}}\right)$ ；

对于顶点朝下的三角形，若要“扩展”，三种情况分别为 $\left(x,y+\frac{l}{\sqrt{3}}\right)$ , $\left(x-\frac{\ell}{2},y-\frac{l}{2\sqrt{3}}\right)$ , $\left(x+\frac{\ell}{2},y-\frac{l}{2\sqrt{3}}\right)$ 。我们将已经选中的三角形用这种方式“扩展”，且不能选择已选中的点。

🍔假设

$S_0$ 为多边形本身

$S_{1}=\left \{S_{11}\cup S_{12}\cup \cdots\cup S_{1j}|j=1,2, \cdots,n_1\right \}$ 为环带 $1$ ；

$S_{2}=\left \{S_{21}\cup S_{22}\cup \cdots\cup S_{2j}|j=1,2, \cdots,n_2\right \}$ 为环带 $2$ ；

$S_{k}=\left \{S_{k1}\cup S_{k2}\cup \cdots\cup S_{kj}|j=1,2, \cdots,n_k\right \}$ 为环带 $k$ 。

$k$ 为该多边形对应的最大环带数，即Heesch数。

🍔约束条件

$S_{0}=S_{1j}=\cdots =S_{kj}$ ， $S_{k1}=S_{k2}=\cdots =S_{kj}$

$S_{0}\cap S_{1}\cap...\cap S_{k-1}\cap S_{k}=0$ ， $S_{k1}\cap S_{k2}\cap...\cap S_{k(j-1)}\cap S_{kj}=0$

$S_{0}\cup S_{1}\cup...\cup S_{k-1}\cup S_{k}$ 是一个单连通多边形，

$S_k$ 包围 $S_{ k-1 }$

🍔生成环带 $S_{k}$

由于生成的原始图形 $S_{0}$ 是由正三角形组成的，那么对于任意副本 $S_\mathrm{kj}$ ,在形成环带时，相对 $S_{0}$ 的旋转角只有0°、60°、120°、180°、240°、300°这 6 种可能性。

🍔最优化

如何排列环带使 $k$ 最大

🍕由正方形组成

[2105.09438] Heesch Numbers of Unmarked Polyforms

🍔生成原始图形 $S_{0}$

这样的原始图形又被称为多联骨牌。多联骨牌（Polyominoes）是由多个正方形以边相连构成的平面图形，在组合数学、计算几何和理论计算机科学等领域有着广泛的应用。在多联骨牌的研究中，生成特定形状或规模的多联骨牌是一个重要的基础问题。

生成多联骨牌有三种方案。

边扩展法

先生成一个正方形，为初代图形，命名为 $squ_1$ ,有四条边分别命名为 $e_1,e_2,e_3,e_4$ ,将这四条边存入边的集合 $G$ 。

我们在这里随机选择一条边，在这条边的基础上生成一个不与原图形重叠的正方形，将新生成的图形命名为 $squ_1+squ_2$ 。

将新加的正方形的边加入边的集合 $G$ ,刚刚选择的边变为图形内部的一部分，从 $G$ 中删除，然后重新命名 $squ_1+squ_2$ 的六条边为 $e_1,e_2,e_3,e_4,e_5,e_6$

…………

这里注意，我们要先设置好组成原始图形 $S_{0}$ 的的正方形个数 $U$ 。

基于邻域扩展的多联骨牌坐标生成算法

该算法基于邻域扩展的思想，构造二维直角坐标系，将每一个正方形用左下点坐标表示，从一个边长为 $\ell$ 的初始正方形开始，逐步在其邻域中选择新的正方形来构建多联骨牌。每次扩展时，只考虑当前已有的正方形的四个邻域方向(上、下、左、右),即新坐表可能为 $(x+\ell,y),(x,y+\ell),(x-\ell,y),(x,y-\ell)$ ,且不能选择已选中的点，确保生成的正方形是相互连接的，然后得到了一些待选坐标。在选择新坐标时，从待选坐标中随机选择一个坐标，这引入了一定的随机性。然而，整个算法的框架是确定的，即通过邻域扩展的方式逐步生成多联骨牌。这种随机性与确定性的结合使得算法能够生成多种不同形状的联骨牌。

基于随机游走的多联骨牌坐标生成算法

本算法设计理念融合了随机探索与局部困境处理机制，以确保生成的多联骨牌既满足连通性要求，又具备一定的随机性与多样性。算法起始于二维平面原点坐标，以此为种子点开启坐标扩展进程。在整个坐标生成流程中，定义了一组表示平面基本方向的向量集，涵盖向上、向下、向右以及向左四个方向，以此为基础构建坐标扩展的方向选择框架。在每一轮坐标扩展迭代中，算法优先对当前坐标点的邻域方向进行可用性评估。对于当前坐标点，依据预定义的方向向量集，依次推算出各个方向上的潜在新坐标。通过与已生成坐标集进行比对，筛选出尚未被访问过的方向，这些方向即构成当前坐标点的可用方向集。若当前坐标点存在可用方向，算法将引入随机性因素，从可用方向集中随机抽取一个方向作为本次扩展的方向选择。基于选定的方向，更新当前坐标点至新的位置，并将该新坐标纳入已生成坐标集，从而实现坐标集的逐步扩充。然而，在坐标扩展进程中，可能会遭遇局部死胡同困境，即当前坐标点的所有邻域方向均已被访问，无可用方向可供选择。针对此类情形，算法设计了一套回溯与重选机制。具体而言，算法遍历已生成坐标集中的所有坐标点，针对每个坐标点重新评估其邻域方向的可用性，统计每个坐标点仍具扩展潜力的方向数量。将具有非零扩展潜力方向数量的坐标点收集至候选坐标点集。若候选坐标点集非空，则从中随机选定一个坐标点作为新的当前坐标点，以此为起点继续坐标扩展流程；反之，若候选坐标点集为空，则意味着算法在当前条件下无法成功生成连通的多联骨牌，算法将触发异常终止信号。通过反复执行上述迭代步骤，直至已生成坐标集的规模达到指定坐标点，即原始图形达到指定的正方形数。