基本思想
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
分而治之
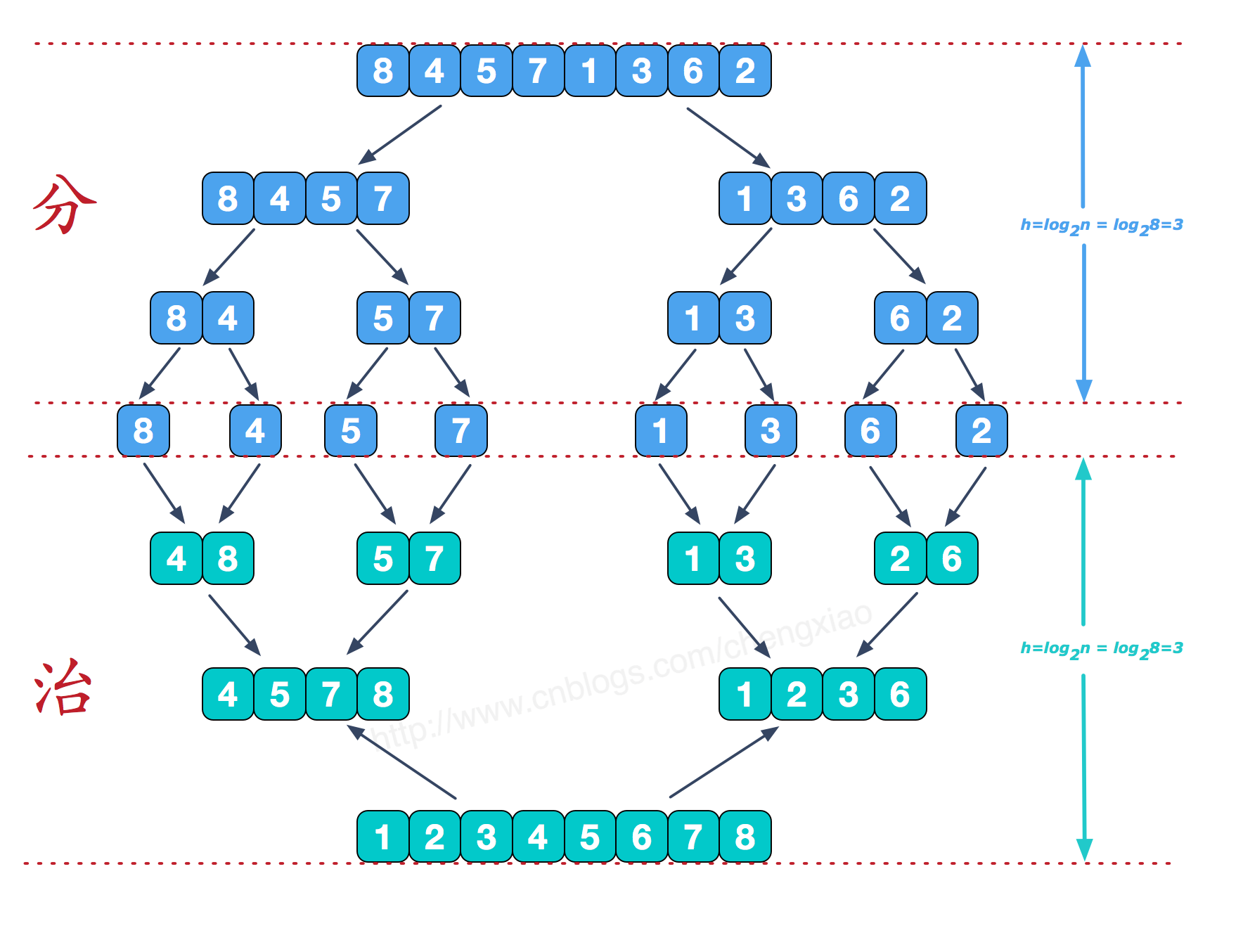
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
合并相邻有序子序列
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
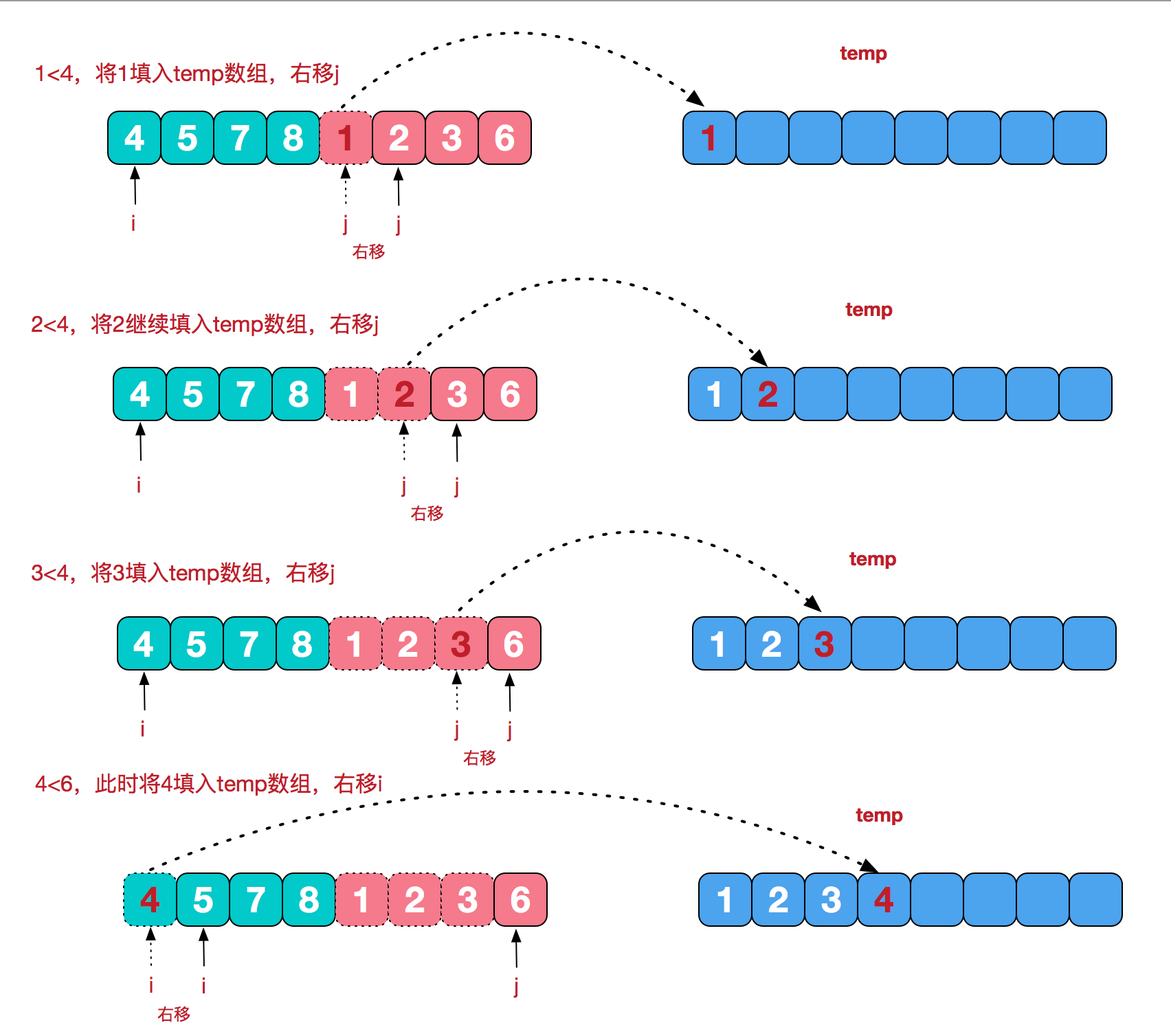
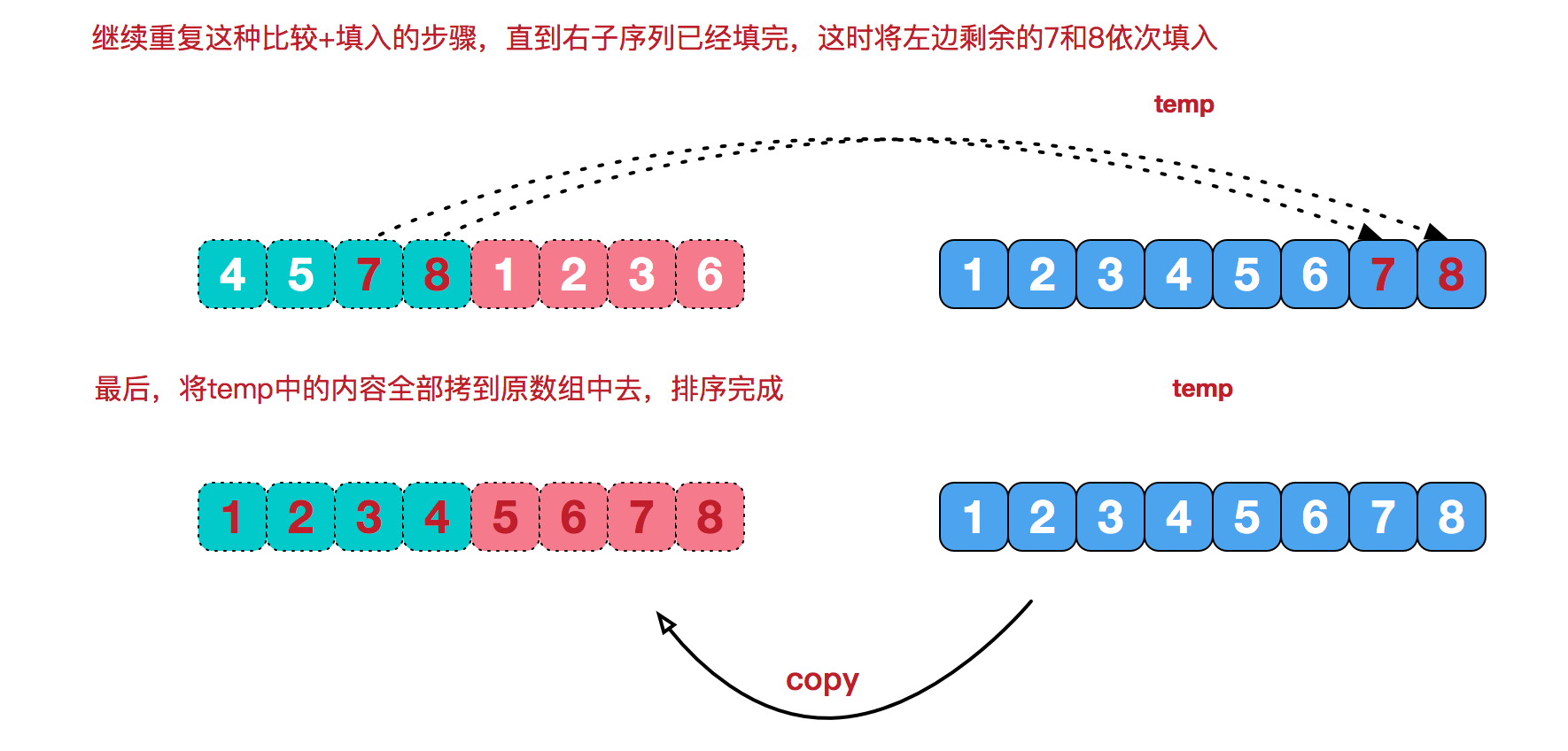







 本文深入讲解了归并排序的基本思想及其实现过程,包括分治策略的运用、递归实现方式、合并相邻有序子序列的具体步骤,以及算法的时间复杂度分析。
本文深入讲解了归并排序的基本思想及其实现过程,包括分治策略的运用、递归实现方式、合并相邻有序子序列的具体步骤,以及算法的时间复杂度分析。
















 1293
1293

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








