目录
梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
导包
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline方程
lambda函数
f = lambda x : (x - 3)**2 + 2.5*x -7.5画图
x = np.linspace(-2,5,100)
y = f(x)
plt.plot(x,y)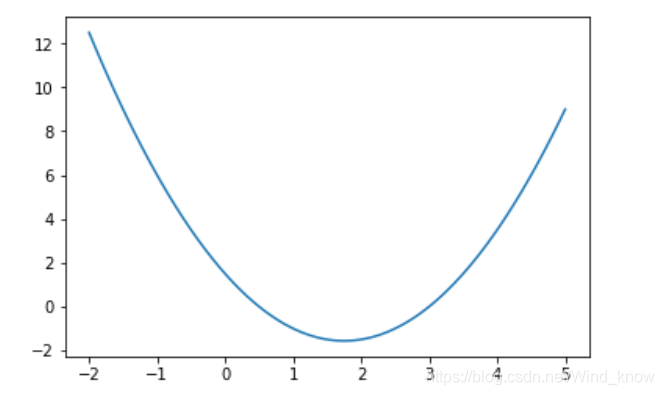
对f求导
求解导数令导数=0求解最小值

梯度下降求解最小值
用lambda表示求导后的方程
# 导数函数
d = lambda x : 2*(x - 3) + 2.5设置学习率
# 学习率,每次改变数值的时候,改变多少
learning_rate = 0.1梯度下降找最优值
# min_value瞎蒙的值,方法,最快的速度找到最优解(梯度下降)
min_value = np.random.randint(-3,5,size = 1)[0]
print('-------------------',min_value)
# 记录数据更新了,原来的值,上一步的值,退出条件
min_value_last = min_value + 0.1
# tollerence容忍度,误差,在万分之一,任务结束
tol = 0.0001
count = 0
while True:
if np.abs(min_value - min_value_last) < tol:
break
# 梯度下降
min_value_last = min_value
# 更新值:梯度下降
min_value = min_value - learning_rate*d(min_value)
count +=1
print('+++++++++++++++++++++%d'%(count),min_value)
print('**********************',min_value)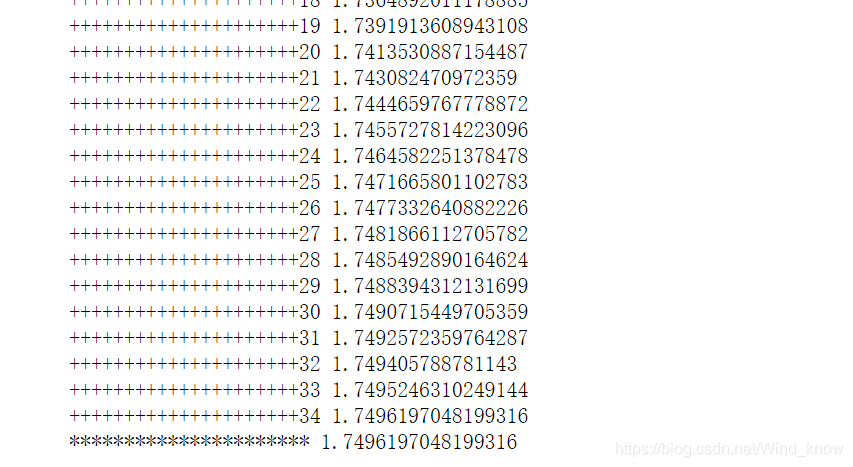
梯度上升找最大值
函数二,有最大值
f2 = lambda x : -(x - 3)**2 + 2.5*x -7.5
x = np.linspace(-2,10,100)
y = f2(x)
plt.plot(x,y)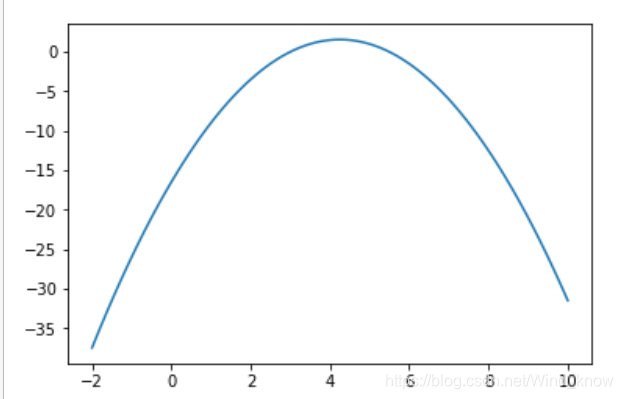
# 梯度提升
# 导数函数
result = []
d2 = lambda x : -2*(x - 3) + 2.5
learning_rate = 10
# max_value瞎蒙的值,方法,最快的速度找到最优解(梯度下降)
# 梯度消失,梯度爆炸(因为学习率太大)
max_value = np.random.randint(2,8,size = 1)[0]
# max_value = 1000
result.append(max_value)
print('-------------------',max_value)
# 记录数据更新了,原来的值,上一步的值,退出条件
max_value_last = max_value + 0.001
# tollerence容忍度,误差,在万分之一,任务结束
# precision精确度,精度达到了万分之一,任务结束
precision = 0.0001
count = 0
while True:
if count >3000:
break
if np.abs(max_value - max_value_last) < precision:
break
# 梯度上升
max_value_last = max_value
# 更新值:梯度上升
max_value = max_value + learning_rate*d2(max_value)
result.append(max_value)
count +=1
print('+++++++++++++++++++++%d'%(count),max_value)
print('**********************',max_value)
更新规则
# 更新规则
ret = ret - ret*step将每一步怎么走的过程画出来 ,加入result[]
# 梯度提升
# 导数函数
d2 = lambda x : -2*(x - 3) + 2.5
learning_rate = 0.1
# max_value瞎蒙的值,方法,最快的速度找到最优解(梯度下降)
# 梯度消失,梯度爆炸(因为学习率太大)
max_value = np.random.randint(2,8,size = 1)[0]
# max_value = 1000
result.append(max_value)
print('-------------------',max_value)
# 记录数据更新了,原来的值,上一步的值,退出条件
max_value_last = max_value + 0.001
# tollerence容忍度,误差,在万分之一,任务结束
# precision精确度,精度达到了万分之一,任务结束
precision = 0.0001
count = 0
while True:
if np.abs(max_value - max_value_last) < precision:
break
# 梯度上升
max_value_last = max_value
# 更新值:梯度上升
max_value = max_value + learning_rate*d2(max_value)
result.append(max_value)
count +=1
print('+++++++++++++++++++++%d'%(count),max_value)
print('**********************',max_value)
画图
plt.figure(figsize=(12,9))
x = np.linspace(4,8,100)
y = f2(x)
plt.plot(x,y)
##列表无法参加运算,将它转化为np
result = np.asarray(result)
plt.plot(result,f2(result),'*')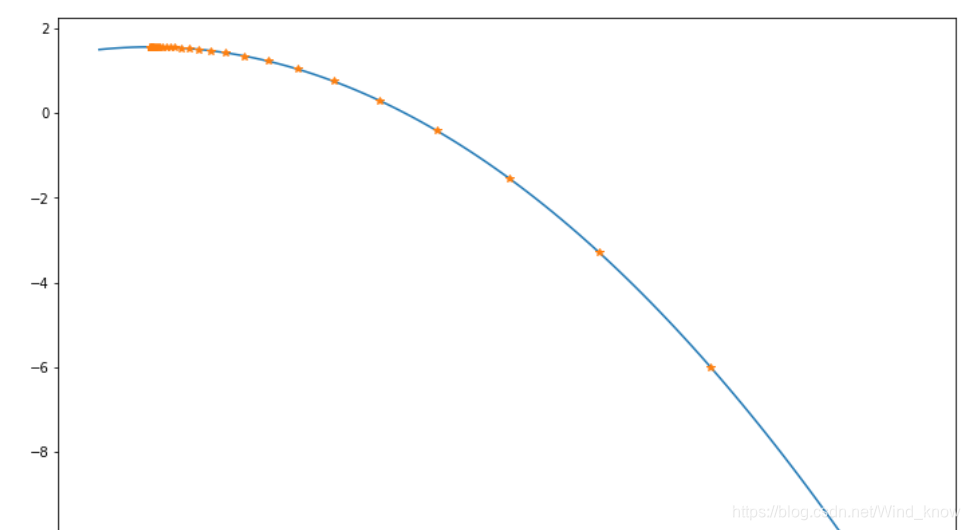
越接近最大值,斜率就越靠近0。leaning_rate设置太大,步子太大,一下就迈过去了。学习率给太大,会造成梯度爆炸,太小会造成梯度消失。
























 4637
4637

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








