leetcode 第399题 除法求值

leetcode 第399题 除法求值

问题分析

问题如下（传送门）

题目给了一组方程式，每个方程式有两个变量，分别为被除数和除数，最后的商在对应位置的方程式结果中。最后求的就是在问题方程式中解出每个方程。这个题目可以用并查集的方法来解决，我们可以将具有联系的所有变量归类到同一个集合中，在一个集合中，任意两个变量直接的关系都可以得到，所有只要问题方程式中的两个变量在同一个集合就能很方便的得到两者的商。
下面的问题就是用什么数据结构来构建这样的集合。开始，我用的是一个长度为26的数组，这样每个字母对应唯一的位置，但是后来提交的时候失败了，因为题目所给的变量并不是全部有单一的字母构成的，其实变量是字符串。所有，后来我就换成用字典来求解了。在字典中，键为当前字符串变量，值为一个列表，其中第一个值为当前键的父亲（形象一点），初始化时就为自己本身，第二个值时父亲与当前键的比值，初始化为1.0，如下所示。

接下来就是构建集合了，假设给定的方程式为[ [“a”, “b”], [“b”, “c”]]，我们可以得到下面的结构：

其中b的父亲为a，b的值为（“a”, a/b），c开始的父亲为b，所以c的值为（“b”, b/c），但后来将c的父亲指向a，如果将c的父亲指向a，那么c值的第二项就要改为a/c，可以通过a/b * b/c得到，这样做对以后的计算很有帮助，因为可以很快速的找到其父亲。
上面的情况中，如果在这条父子链上，多出分支的话，可以直接加入，即假设方程式为[ [“a”, “b”], [“b”, “c”], [“b”, “e”]]，得到字典如下：

同样，改变e的父亲到a。

上面是所有的变量构成了一个集合，下面是有两个集合的情况。假设方程式为[ [“a”, “b”], [“b”, “c”],[“b”, “e”], [“f”, “g”]]，那么结果为：

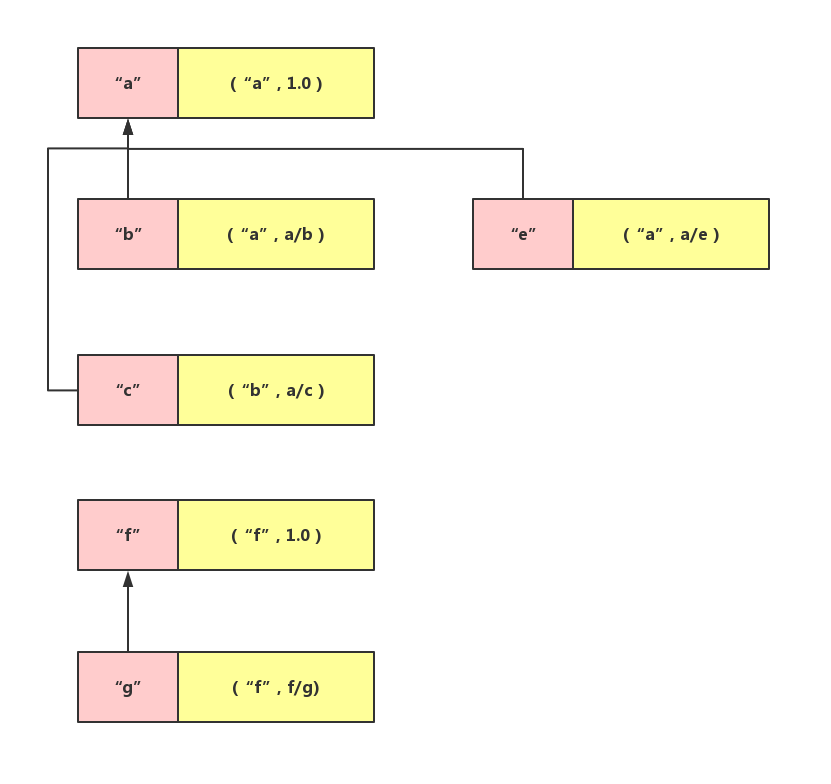
接下来就是比价重要的点了，假设在给定方程式中先建立了两个不同的集合，但是有一个方程式将两个集合联系到一起那该怎么办，比如方程式为：[ [“a”, “b”], [“b”, “c”], [“b”, “e”], [“f”, “g”], [“c”, “g”]]。通过c和g将两个集合合并成一个，这里我的做法是，找到两个结合的父亲，然后让其中一个父亲降级，成为另一个父亲的儿子，这里，我让f成为了a的儿子，那么得到示意图如下：

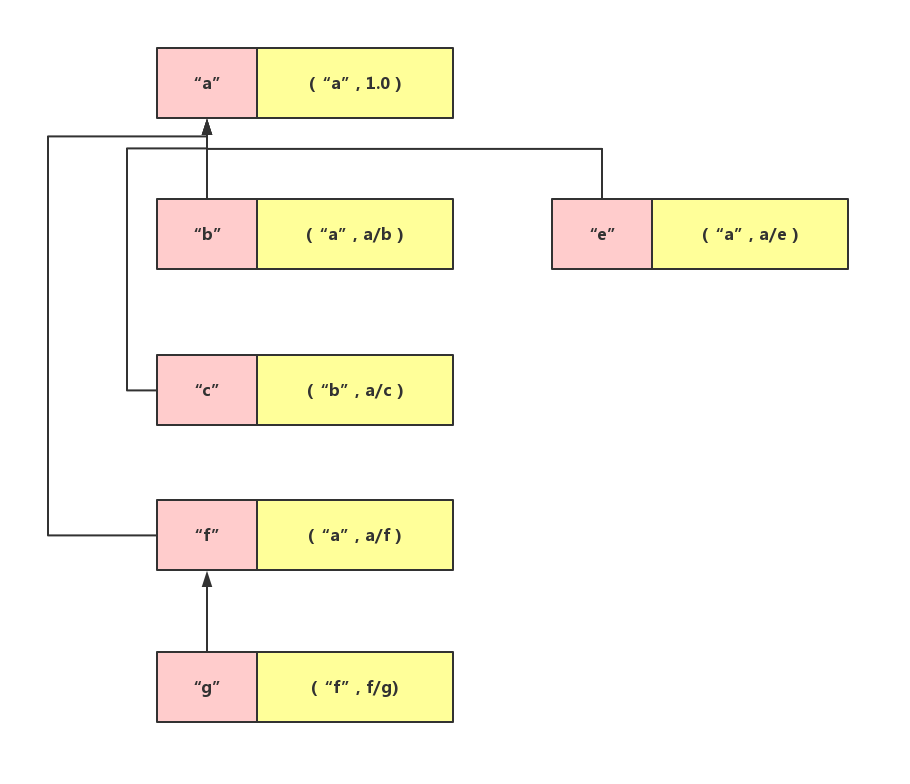
我们知道如下项：a/c， c/g， f/g所以一定能得到a/f（数学运算）。至此，所有的变量都联通了。

下面就是对问题方程式求值的过程。由于所有在同一个集合的变量都有同一个祖先，我们就可以利用这个祖先做一个中间项。比如b/g。可以用下面的手段得到：

所以只要是同一个集合，一定得到确切的值，不在同一个集合的或在方程式中没有出现的变量，直接返回-1.0。

源码

Python

class Solution:
    def calcEquation(self, equations, values, queries):
        conn = {}
        ret = []

        def findFather(i):
            multi = 1
            while conn[i][0] != i:
                multi *= conn[i][1]
                i = conn[i][0]
            return i, multi


        for i, equ in enumerate(equations):
            a, b = equ
            if a in conn:
                father_1, num_1 = findFather(a)
                num_2 = 1
                father_2 = b
                if b in conn:
                    father_2, num_2 = findFather(b)
                conn[father_2] = father_1, num_1 * values[i] / num_2
            else:
                conn[a] = [a, 1]
                num_2 = 1
                father_2 = b
                if b in conn:
                    father_2, num_2 = findFather(b)
                conn[father_2] = a, values[i] / num_2

        for query in queries:
            a, b = query
            if a in conn and b in conn:
                father_1, num_1 = findFather(a)
                father_2, num_2 = findFather(b)
                if  father_1 == father_2:
                    ret.append(num_2 / num_1)
                    continue
            ret.append(-1.0)

        return ret

C++

class Solution {
    map<string, pair<string, double>> conn;
    string father_2, father_1, a, b;
    double num_1, num_2;
    pair<string, double> ans_1, ans_2;

    pair<string, double> findFather(string i){
        double multi = 1.0;
        while (conn[i].first != i){
            multi *= conn[i].second;
            i = conn[i].first;
        }
        return make_pair(i, multi);

    }
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        vector<double> ret;
        for (int i = 0; i < equations.size(); ++i){
            a = equations[i][0];
            b = equations[i][1];
            if (conn.find(a) != conn.end()){
                ans_1 = findFather(a);
                father_1 = ans_1.first;
                num_1 = ans_1.second;
                father_2 = b;
                num_2 = 1.0;
                if (conn.find(b) != conn.end()){
                    pair<string, double> ans_2 = findFather(b);
                    father_2 = ans_2.first;
                    num_2 = ans_2.second;
                }
                conn[father_2] = make_pair(father_1, num_1 * values[i] / num_2);
            }

            else{
                conn[a] = make_pair(a, 1.0);
                father_2 = b;
                num_2 = 1.0;
                if (conn.find(b) != conn.end()){
                    pair<string, double> ans_2 = findFather(b);
                    father_2 = ans_2.first;
                    num_2 = ans_2.second;
                }
                conn[father_2] = make_pair(a, values[i] / num_2);
            }
        }

        for (auto query: queries){
            a = query[0];
            b = query[1];
            if (conn.find(a) != conn.end() && conn.find(b) != conn.end()){
                ans_1 = findFather(a);
                ans_2 = findFather(b);
                if (ans_1 .first == ans_2.first){
                    ret.push_back(ans_2.second / ans_1.second);
                    continue;
                }
            }
            ret.push_back(-1.0);
        }

        return ret;
    }
};

谢谢！！