【轻松掌握数据结构与算法】栈：后进先出的数据结构

已于 2025-01-12 16:21:01 修改
阅读量1.1k 收藏 19
点赞数 20
CC 4.0 BY-SA版权
分类专栏： 轻松掌握数据结构与算法 文章标签： python 开发语言 数据结构 算法
于 2025-01-12 01:19:06 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Whoisbug/article/details/145085299

栈（Stack）是一种后进先出（LIFO, Last In First Out）的数据结构，它只允许在一端进行插入和删除操作。栈在计算机科学中有着广泛的应用，例如函数调用、表达式求值、括号匹配等。本文将详细介绍栈的基本概念、操作以及应用场景，并通过示例和图表来帮助你更好地理解栈。

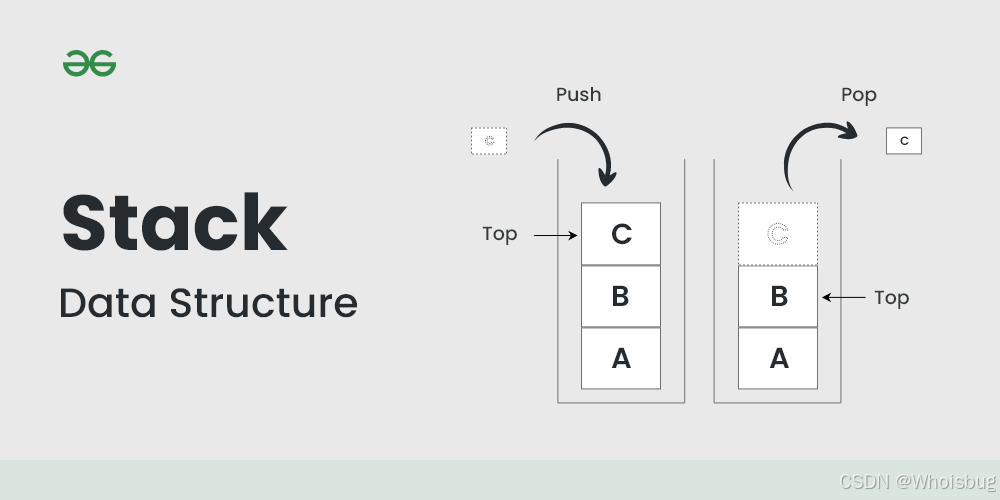
栈的基本概念

栈是一种线性数据结构，它遵循后进先出的原则。栈的主要操作包括：

  • push：将一个元素添加到栈顶。

  • pop：移除栈顶的元素并返回。

  • peek 或 top：返回栈顶的元素但不移除。

  • is_empty：检查栈是否为空。

  • size：返回栈中元素的数量。

栈的实现

栈可以通过数组或链表来实现。数组实现的栈具有固定的大小，而链表实现的栈可以动态扩展。

数组实现的栈
class Stack:
    def __init__(self, capacity):
        self.capacity = capacity
        self.stack = [None] * capacity
        self.top = -1

    def push(self, value):
        if self.top == self.capacity - 1:
            raise Exception("Stack overflow")
        self.top += 1
        self.stack[self.top] = value

    def pop(self):
        if self.top == -1:
            raise Exception("Stack underflow")
        value = self.stack[self.top]
        self.top -= 1
        return value

    def peek(self):
        if self.top == -1:
            return None
        return self.stack[self.top]

    def is_empty(self):
        return self.top == -1

    def size(self):
        return self.top + 1
链表实现的栈
class ListNode:
    def __init__(self, value=0, next=None):
        self.value = value
        self.next = next

class Stack:
    def __init__(self):
        self.head = None

    def push(self, value):
        new_node = ListNode(value)
        new_node.next = self.head
        self.head = new_node

    def pop(self):
        if self.head is None:
            raise Exception("Stack underflow")
        value = self.head.value
        self.head = self.head.next
        return value

    def peek(self):
        if self.head is None:
            return None
        return self.head.value

    def is_empty(self):
        return self.head is None

    def size(self):
        count = 0
        current = self.head
        while current:
            count += 1
            current = current.next
        return count

栈的操作示意图

1. push 操作

概念：将一个元素添加到栈顶。

示意图：

初始状态：
栈顶
+---+    push(3)
|   |    +---+
|   |    | 3 |
|   |    |   |
+---+    +---+

2. pop 操作

概念：移除栈顶的元素并返回。

示意图：

初始状态：
栈顶
+---+    pop()
| 3 |    +---+
| 2 |    | 2 |
| 1 |    | 1 |
+---+    +---+

3. peek 操作

概念：返回栈顶的元素但不移除。

示意图：

初始状态：
栈顶
+---+    peek()
| 3 |    返回 3
| 2 |
| 1 |
+---+

4. is_empty 操作

概念：检查栈是否为空。

示意图：

初始状态：
栈顶
+---+    is_empty()
| 3 |    返回 False
| 2 |
| 1 |
+---+

空栈：
栈顶
+---+    is_empty()
|   |    返回 True
+---+

5. size 操作

概念：返回栈中元素的数量。

示意图：

初始状态：
栈顶
+---+    size()
| 3 |    返回 3
| 2 |
| 1 |
+---+

栈的应用场景

栈在许多计算机科学问题中都有广泛的应用。以下是一些常见的应用场景和详细的示例。

1. 括号匹配

括号匹配问题是一个经典的栈应用。给定一个字符串，包含多种类型的括号（如()、[]、{}），需要检查括号是否正确匹配。

def is_valid_parentheses(s):
    stack = []
    mapping = {")": "(", "]": "[", "}": "{"}
    for char in s:
        if char in mapping:
            top_element = stack.pop() if stack else '#'
            if mapping[char] != top_element:
                return False
        else:
            stack.append(char)
    return not stack

# 示例
print(is_valid_parentheses("()"))  # True
print(is_valid_parentheses("()[]{}"))  # True
print(is_valid_parentheses("(]"))  # False
print(is_valid_parentheses("([)]"))  # False
print(is_valid_parentheses("{[]}"))  # True

2. 表达式求值

栈可以用于计算算术表达式的值，特别是处理包含括号的表达式。以下是一个示例，展示如何使用栈来计算中缀表达式的值。

def precedence(op):
    if op in ('+', '-'):
        return 1
    if op in ('*', '/'):
        return 2
    return 0

def apply_op(a, b, op):
    if op == '+': return a + b
    if op == '-': return a - b
    if op == '*': return a * b
    if op == '/': return a // b

def evaluate(expression):
    numbers = []
    ops = []
    i = 0
    while i < len(expression):
        if expression[i] == ' ':
            i += 1
            continue
        elif expression[i] == '(':
            ops.append(expression[i])
        elif expression[i].isdigit():
            val = 0
            while i < len(expression) and expression[i].isdigit():
                val = val * 10 + int(expression[i])
                i += 1
            numbers.append(val)
            i -= 1
        elif expression[i] == ')':
            while ops[-1] != '(':
                op = ops.pop()
                val2 = numbers.pop()
                val1 = numbers.pop()
                numbers.append(apply_op(val1, val2, op))
            ops.pop()
        else:
            while (len(ops) != 0 and precedence(ops[-1]) >= precedence(expression[i])):
                op = ops.pop()
                val2 = numbers.pop()
                val1 = numbers.pop()
                numbers.append(apply_op(val1, val2, op))
            ops.append(expression[i])
        i += 1
    while len(ops) != 0:
        op = ops.pop()
        val2 = numbers.pop()
        val1 = numbers.pop()
        numbers.append(apply_op(val1, val2, op))
    return numbers[0]

# 示例
print(evaluate("10 + 2 * 6"))  # 22
print(evaluate("100 * 2 + 12"))  # 212
print(evaluate("100 * ( 2 + 12 )"))  # 1400
print(evaluate("100 * ( 2 + 12 ) / 14"))  # 100

3. 函数调用栈

在编程语言中，函数调用是通过栈来管理的。每次调用函数时，都会在栈上创建一个新的帧，包含函数的局部变量和返回地址。当函数返回时，当前帧被弹出，控制权返回到调用者。以下是一个简单的示例，展示如何使用栈来模拟函数调用。

def factorial(n):
    if n == 0 or n == 1:
        return 1
    return n * factorial(n - 1)

# 模拟函数调用栈
call_stack = []
call_stack.append(("factorial", 5))
while call_stack:
    func, arg = call_stack.pop()
    if arg == 0 or arg == 1:
        result = 1
    else:
        call_stack.append(("multiply", (arg, call_stack)))
        call_stack.append(("factorial", arg - 1))
        continue
    while call_stack and call_stack[-1][0] == "multiply":
        _, (n, prev_call_stack) = call_stack.pop()
        result *= n
        call_stack = prev_call_stack
    if call_stack:
        call_stack[-1] = (call_stack[-1][0], result)
    else:
        print(result)

# 输出结果
120

4. 逆波兰表达式求值

逆波兰表达式（RPN）是一种不需要括号来表示运算符优先级的表达式。栈可以用于高效地计算逆波兰表达式的值。

def evaluate_rpn(tokens):
    stack = []
    for token in tokens:
        if token in "+-*/":
            b = stack.pop()
            a = stack.pop()
            if token == '+':
                stack.append(a + b)
            elif token == '-':
                stack.append(a - b)
            elif token == '*':
                stack.append(a * b)
            elif token == '/':
                stack.append(int(a / b))
        else:
            stack.append(int(token))
    return stack[0]

# 示例
print(evaluate_rpn(["2", "1", "+", "3", "*"]))  # 9
print(evaluate_rpn(["4", "13", "5", "/", "+"]))  # 6
print(evaluate_rpn(["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]))  # 22

5. 最小栈

设计一个支持 push、pop、top 操作，并能在常数时间内检索到最小元素的栈。

class MinStack:
    def __init__(self):
        self.stack = []
        self.min_stack = []

    def push(self, x):
        self.stack.append(x)
        if not self.min_stack or x <= self.min_stack[-1]:
            self.min_stack.append(x)

    def pop(self):
        if self.stack:
            if self.stack[-1] == self.min_stack[-1]:
                self.min_stack.pop()
            return self.stack.pop()
        raise Exception("Stack underflow")

    def top(self):
        if self.stack:
            return self.stack[-1]
        raise Exception("Stack underflow")

    def getMin(self):
        if self.min_stack:
            return self.min_stack[-1]
        raise Exception("Stack underflow")

# 示例
min_stack = MinStack()
min_stack.push(-2)
min_stack.push(0)
min_stack.push(-3)
print(min_stack.getMin())  # -3
min_stack.pop()
print(min_stack.top())  # 0
print(min_stack.getMin())  # -2

总结

栈是一种灵活的数据结构，适用于需要动态大小和高效插入、删除操作的场景。通过理解栈的基本概念和操作，你可以更好地应用栈来解决实际问题。希望本文的示例和图表能帮助你更好地理解和掌握栈。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值