NeuDs 数据结构月考 3-优快云博客

本文链接：https://blog.youkuaiyun.com/WeFun_Han/article/details/131032207

NeuDs 数据结构月考 3：图论+排序算法

一.判断题

有向图的邻接矩阵是对称的。F

关于图的遍历

图的深度优先遍历相当于二叉树的先序遍历。T

希尔排序是稳定的算法。F

如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G中一定有回路。F

图是表示一对一关系的数据结构。F

多对多的数据结构

快速排序是稳定的算法。F

不稳定排序

排序的稳定性是指排序算法中的比较次数保持不变，且算法能够终止。F

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r [i]=r [j]，且r [i]在r [j]之前，而在排序后的序列中，r [i]仍在r [j]之前，则称这种排序算法是稳定的。

最小生成树问题是构造连通网的最小代价生成树。T

对于带权无向图 G = (V, E)，M 是 G 的最小生成树，则 M 中任意两点 V1 到 V2 的路径一定是它们之间的最短路径。F

最小生成树是总权值最小，不是任意两点间权值最小

查找某元素时，折半查找法的查找速度一定比顺序查找法快。F

特定情况下效率一样

当查找表中元素个数为1个或2个时，二分法和顺序法速度相等；当元素个数大于2个时，二分法更快。（前提是有序表）

任何最小堆的前序遍历结果是有序的（从小到大）。F

若有向图不存在回路，即使不用访问标志位同一结点也不会被访问两次。F

错。若一个顶点入度大于 1，则会被访问两次

对N（≥2）个权值均不相同的字符构造哈夫曼树，则树中任一非叶结点的权值一定不小于下一层任一结点的权值。T

（权值均不相等) 哈夫曼树：

1.树中一定没有度为1的节点

2.哈夫曼树不一定是完全二叉树

3.树中任一非叶节点的权值一定不小于下一层任一节点的权值

在任一有向图中，所有顶点的入度之和等于所有顶点的出度之和。T

在任一有向图中，所有顶点的入度之和等于所有顶点的出度之和。

如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G中一定有回路。F

有两个连通分量才需要两次广搜

无向连通图所有顶点的度之和为偶数。T

二.单选题

1.对于序列{ 49，38，65，97，76，13，27，50 }，按由小到大进行排序，下面哪一个是初始步长为4的希尔排序法第一趟的结果？

A.49,13,27,50,76,38,65,97

B.49,76,65,13,27,50,97,38

C.13,27,38,49,50,65,76,97

D.97,76,65,50,49,38,27,13

补充知识：希尔排序：间距=步长

2.下列因素中，影响散列（哈希）方法平均查找长度的是

I. 装填因子

II.散列函数

III. 冲突解决策略

A.仅 II、III

B.I、II、III

C.仅 I、III

D.仅 I、II

3.在图中

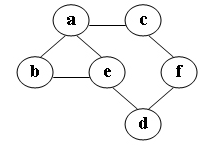
自a点开始进行深度优先遍历算法可能得到的结果为。

A.a,e,d,f,c,b

B.a,c,f,e,b,d

C.a,e,b,c,f,d

D.a,b,e,c,d,f

深度优先搜索就是一路走到底，碰壁了再回头走另外一条路

4.给定有权无向图的邻接矩阵如下，其最小生成树的总权重是：

A.14

B.10

C.11

D.12

5.有组记录的排序码为{46，79，56，38，40，84 }，采用快速排序（以位于最左位置的对象为基准而）得到的第一次划分结果为：

A.{38,79,56,46,40,84}

B.{38,46,79,56,40,84}

C.{40,38,46,56,79,84}

D.{38,46,56,79,40,84}

6.我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题？

A.拓扑排序算法

B.Dijkstra算法

C.深度优先搜索

D.Kruskal算法

7.对N个记录进行堆排序，最坏的情况下时间复杂度是：

A.O(NlogN)

B.O(N)

C.O(logN)

D.O(N^2)

8.若图的邻接矩阵中主对角线上的元素全是0，其余元素全是1，则可以断定该图一定是____。

A.无向图

B.非带权图

C.完全图

D.有向图

解析: 图的邻接矩阵对角线元素必为0，其余元素全为1代表任何两个顶点之间都存在边，也就是完全图。

9.设有一组记录的关键字为{19，14，23，1，68，20，84，27，55，11，10，79}，用链地址法构造散列表，散列函数为H（key）=key MOD 13,散列地址为1的链中有（）个记录。

A.4

B.1

C.3

D.2

10.以下算法中用于求解最小生成树的是（）

A.Dijkstra算法

B.Floyd算法

C.Prim算法

D.深度优先搜索算法

11.使用迪杰斯特拉（Dijkstra）算法求下图中从顶点1到其他各顶点的最短路径，依次得到的各最短路径的目标顶点是：

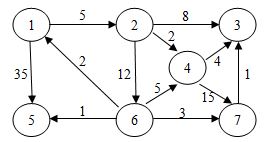
A.2, 5, 3, 4, 6, 7

B.5, 2, 6, 3, 4, 7

C.2, 3, 4, 5, 6, 7

D.2, 4, 3, 6, 5, 7

12.给定一个图的邻接矩阵如下，则从V1出发的宽度优先遍历序列（BFS，有多种选择时小标号优先）是：

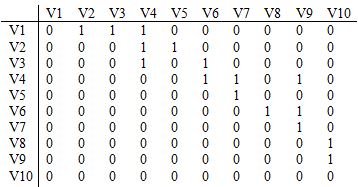
A.V1, V2, V4, V6, V8, V10, V9, V7, V5, V3

B.V1, V2, V3, V4, V5, V6, V7, V9, V8, V10

C.V1, V2, V4, V3, V6, V8, V10, V9, V7, V5

D.V1, V2, V3, V5, V7, V9, V10, V6, V8, V4

13.对于一个具有n个顶点和e条边的无向图，若采用邻接表表示，所有顶点邻接表的边结点总数为（）。

A.2e

B.e/2

C.e

D.n+e

14.下列排序算法中，待排序数据有序时花费时间反而最多的是( )排序。

A.希尔

B.选择

C.快速

D.冒泡

快排在无序时是最快的内部排序算法

快速排序是把数列按一个枢纽值分成两部分分别排序，所以效率高。但是若原数据为有序，并且选择的枢纽值为第一个数时，那在分块时会将一个第一个数前面的数（也就是没有）分为一块，将除第一个数的所有数分成了另一块。这样一来，每一次分块都只减少了一个值，而每次分块的时间为O（N），所以总时间为O（N^2）。

15.用直接插入排序方法对下面四个序列进行排序（由小到大），元素比较次数最少的是（）。

A.21,32,46,40,80,69,90,94

B.94,32,40,90,80,46,21,69

C.90,69,80,46,21,32,94,40

D.32,40,21,46,69,94,90,80

逆序越少的序列，在直接插入排序中比较次数是越少的

16.下面关于图的存储的叙述中正确的是（）

A. 用邻接表法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关
B. 用邻接表法存储图，占用的存储空间大小与图中边数和结点个数都有关
C. 用邻接矩阵法存储图，占用的存储空间大小与图中结点个数和边数都有关
D. 用邻接矩阵法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关

链接：下面关于图的存储的叙述中正确的是（）__牛客网
来源：牛客网

（1）、邻接矩阵

使用的是两个数来表示图，一个一位数组的存储顶点的信息，一个二维数组（邻接矩阵）存储图中的边或者是弧的信息

设图有n个顶点，则邻接矩阵是一个n * n的方阵！

所以总结下来邻接矩阵只跟图的顶点有关！

（2）、邻接表

使用数组 + 链表的方式来存储图

图中的顶点使用一维数组来存储，图中每个顶点的所有邻节点构成一个线性表，邻接点的个数是不确定的，所以使用单链表来存储

所有总结下来邻接表既和顶点有关也和变有关！

三.函数题

R6-1 有向图出度为0的顶点个数

，统计有向图中出度为0的顶点个数。

函数接口定义：

int GetCount(MGraph G);

G为采用邻接矩阵作为存储结构的有向图，函数GetCount返回G中出度为0的顶点个数，如果没有顶点出度为0，则返回0。

裁判测试程序样例：

#include <stdio.h> #define MVNum 100 //最大顶点数 typedef struct { char vexs[MVNum]; //存放顶点的一维数组 int arcs[MVNum][MVNum]; //邻接矩阵 int vexnum, arcnum; //图的当前顶点数和边数 }MGraph; int GetCount(MGraph G); void CreatMGraph(MGraph *G);/* 创建图 */ int main() { MGraph G; CreatMGraph(&G); printf("%d:%d\n",G.vexnum, GetCount(G)); return 0; } void CreatMGraph(MGraph *G) { int i, j, k; scanf("%d%d", &G->vexnum, &G->arcnum); getchar(); for (i = 0; i < G->vexnum; i++) scanf("%c", &G->vexs[i]); for (i = 0; i < G->vexnum; i++) for (j = 0; j < G->vexnum; j++) G->arcs[i][j] = 0; for (k = 0; k < G->arcnum; k++) { scanf("%d%d", &i, &j); G->arcs[i][j] = 1; } } /* 你的代码将被嵌在这里 */

输入样例：

例如有向图

第一行给出图的顶点数n和弧数e。第二行给出n个字符，表示n个顶点的数据元素的值。后面是e行，给出每一条弧的两个顶点编号。

输出样例：

输出为一行，包括两个整数，第一个为顶点个数，第二个为出度为0的顶点个数，中间用冒号分隔。

4:1

代码：

int GetCount(MGraph G)
{
    int cnt=0;//用于计算出度为0的个数
    for(int i=0;i<G.vexnum;i++)
    {
        int sum=0;
        for(int j=0;j<G.vexnum;j++)
        {
            sum+=G.arcs[i][j];
        }
        if(sum==0)cnt++;
    }
    return cnt;
    
}

R6-2 简单选择排序

本题要求实现简单选择排序函数，待排序列的长度1<=n<=1000。

函数接口定义：

void SelectSort(SqList L);

其中L是待排序表，使排序后的数据从小到大排列。
###类型定义：

typedef int KeyType; typedef struct { KeyType *elem; /*elem[0]一般作哨兵或缓冲区*/ int Length; }SqList;

裁判测试程序样例：

#include<stdio.h> #include<stdlib.h> typedef int KeyType; typedef struct { KeyType *elem; /*elem[0]一般作哨兵或缓冲区*/ int Length; }SqList; void CreatSqList(SqList *L);/*待排序列建立，由裁判实现，细节不表*/ void SelectSort(SqList L); int main() { SqList L; int i; CreatSqList(&L); SelectSort(L); for(i=1;i<=L.Length;i++) { printf("%d ",L.elem[i]); } return 0; } /*你的代码将被嵌在这里 */

输入样例：

第一行整数表示参与排序的关键字个数。第二行是关键字值例如：

10
5 2 4 1 8 9 10 12 3 6

输出样例：

输出由小到大的有序序列，每一个关键字之间由空格隔开，最后一个关键字后有一个空格。

1 2 3 4 5 6 8 9 10 12

代码：



void SelectSort(SqList L)
{
    for(int i=1;i<=L.Length-1;i++)
    {
        int minid=i;
        int j;
        for( j=i+1;j<=L.Length;j++)
        {
            if(L.elem[j]<L.elem[minid])minid=j;
        }
        int temp=L.elem[i];
        L.elem[i]=L.elem[minid];
        L.elem[minid]=temp;
        
    }
}

四.填空题

普里姆算法

请写出用普里姆算法从顶点A出发生成最小生成树每一步加入的边。

(1) AE

(2) ED

(3) DF

(4) FB

(5) FC

注：顶点 X 到 Y 的无向边简记作：XY 或 YX。

五.编程题

R7-1 成绩排序

给出班里某门课程的成绩单，请你按成绩从高到低对成绩单排序输出，如果有相同分数则名字字典序小的在前。

输入格式:

第一行为n (3< n < 200)，表示班里的学生数目；

接下来的n行，每行为每个学生的名字和他的成绩, 中间用单个空格隔开。名字只包含字母且长度不超过20，成绩为一个不大于100的非负整数。

输出格式:

把成绩单按分数从高到低的顺序进行排序并输出，每行包含名字和分数两项，之间有一个空格。

输入样例:

4
Tom 90
Dongdong 90
Ding 92
Tim 28

输出样例:

Ding 92
Dongdong 90
Tom 90
Tim 28

代码：

主要思想就是根据结构体的某个数据进行对结构体的排序，一般的是交换数组元素即可，但这个就是交换结构体；

#include<bits/stdc++.h>
#include<algorithm>
#include<string.h>

using namespace std;

struct Student
{
    string name;
    int mark;
};

//C++中的sort函数比较器//需要包含 algorithm 头文件
bool cmp(const Student& a, const Student& b)
{
    
    if(a.mark!=b.mark)
    {
        return a.mark>b.mark;//从大到小排序
    }else{
        return a.name<b.name;//如果有相同分数则名字字典序小的在前。
    }
}


int main()
{
    int n;
    cin>>n;
    
    Student students[n];

    for(int i=0;i<n;i++)
    {
        
        cin>>students[i].name;
        cin>>students[i].mark;
        
    }
    //c++标准库，函数
    stable_sort(students,students+n,cmp);

    for(int i=0;i<n;i++)
    {
        cout<<students[i].name<<" "<<students[i].mark<<endl;
    }


    return 0;
}

#include <stdio.h>
#include <string.h>
#define N 201

struct node {
    char name[25];
    int score;
}a[N];

int main()
{
    int n, i, j;
    scanf("%d", &n);
    for(i = 0; i < n; ++i)
        scanf("%s%d", a[i].name, &a[i].score);

    for(i = 0; i < n - 1; ++i) {
        for(j = i; j < n; ++j) {
            if(a[j].score > a[i].score || (a[j].score == a[i].score && strcmp(a[j].name, a[i].name) < 0)) {
                struct node tmp = a[i]; a[i] = a[j]; a[j] = tmp;
            }
        }
    }

    for(i = 0; i < n; ++i) printf("%s %d\n", a[i].name, a[i].score);
    return 0;
}