前言
众所周知,模型是由很多个小三角面组成的,而三角面又是由三条边组成的,所以要想渲染模型,第一步是画直线。这一节要详细讲三个经典的直线算法。
在上一讲中我们讨论了如何用 xmake 来做跨平台的编译工作,我对 Windows 和 Mac 平台的编译做了区分:在 win 平台链接下载好的 lib,在 mac 平台使用 brew 来引入 SDL2 的依赖。然后 xmake 的作者 ruki 大佬指出可以直接用 xmake 的 libsdl 包,支持跨平台,可以用优美而一致的代码实现两个平台的配置。
所以文件 xmake.lua 可以改为:
add_rules("mode.debug", "mode.release")
set_languages("c++14")
-- SDL2
add_requires("libsdl")
if is_os("windows") then
-- Avoid for error LINK1561
add_ldflags("/SUBSYSTEM:CONSOLE")
end
target("DLSoftRenderer")
set_kind("binary")
add_includedirs("src/include")
add_files("src/*.cpp")
add_packages("libsdl")
然后我们就可以安心地把 SDL2 的文件夹从项目中移除了,完全交给 xmake 去处理。
概述
由于显示器精度总是有限的,所以在屏幕上只能用离散的点去逼近直线,如下图所示:

直线算法的目标就是以最少的计算量,绘制出最逼近指定直线路径上的最佳像素点。该篇博客主要讲述两种画直线的算法:DDA 算法和 Bresenham 算法。
DDA 算法
第一个要介绍的算法叫做 DDA (Digital Differential Analyzer,数值微分法),顾名思义,该方法是用微积分的思想来画直线。
直线最简单的表示方法为斜截式:
y=kx+t y = kx + t y=kx+t
给定直线的两个端点 P0(x0,y0)P_0(x_0,y_0)P0(x0,y0) 和 P1(x1,y1)P_1(x_1,y_1)P1(x1,y1),则微分形式可以表示为:
k=ΔxΔy=x1−x0y1−y0 k=\frac{\Delta x}{\Delta y}=\frac{x_1-x_0}{y_1-y_0} k=ΔyΔx=y1−y0x1−x0
基本思想是沿着某一个轴递增,计算另一个轴的增量,根据斜率拆解成两种情况:k<1k<1k<1 和 k≥1k\ge1k≥1。
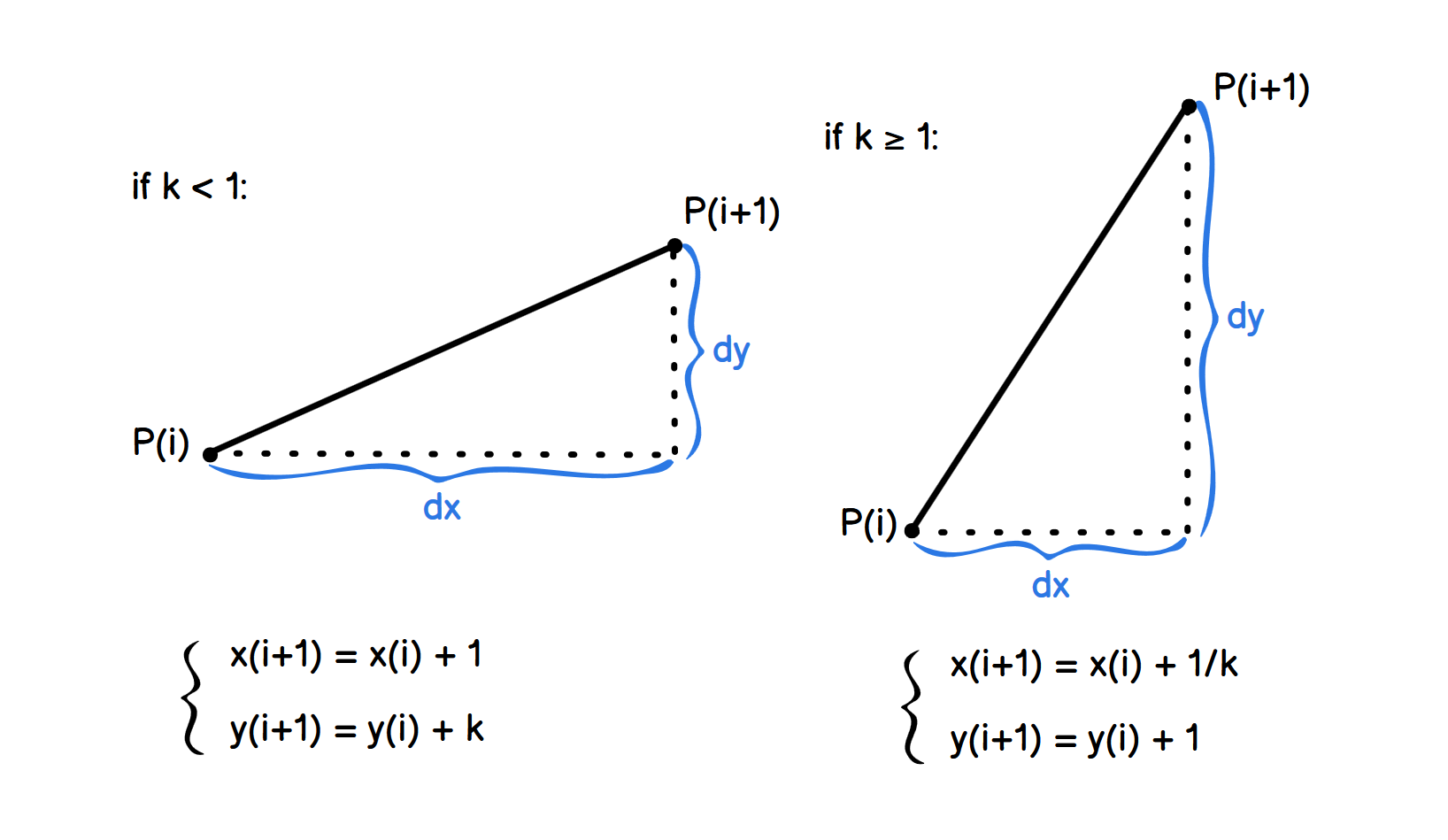
综合考虑两种情况,写成伪代码就是:
DrawLine(x0, y0, x1, y1)
dx = x1 - x0
dy = y1 - y0
step = max(abs(dx), abs(dy))
xIncre = dx / step
yIncre = dy / step
for i from 0 to step
SetPixel(round(x), round(y))
x += xIncre
y += yIncre
DDA 算法的每一步都是在上一步的值加上一个增量来获得的,故称为增量算法,DDA 尽管实现起来很简单,但是计算过程中有浮点数的运算,其效率因此不高。我们的软渲染器不会采用 DDA 算法。
中点 Bresenham 算法
Bresenham 算法才是我们今天的主角,因为它实现了完全无浮点数绘制直线,是现代应用最广范的直线生成算法。接下来我将带着你一步步推导 Bresenham 算法。
首先,直线可以用隐式方程来表示:
F(x,y)=y−kx−t=0 F(x,y)=y-kx-t=0 F(x,y)=y−kx−t=0
如下图所示,Pi(xi,yi)P_i(x_i,y_i)Pi(xi,yi) 是当前点,Pu(xi+1,yi+1)P_u(x_i+1,y_i+1)Pu(xi+1,yi+1) 和 Pd(xi+1,yi)P_d(x_i+1,y_i)Pd(xi+1,yi) 是两个候选点,M(xi+1,yi+0.5)M(x_i+1,y_i+0.5)M(xi+1,yi+0.5) 是候选点的中点。
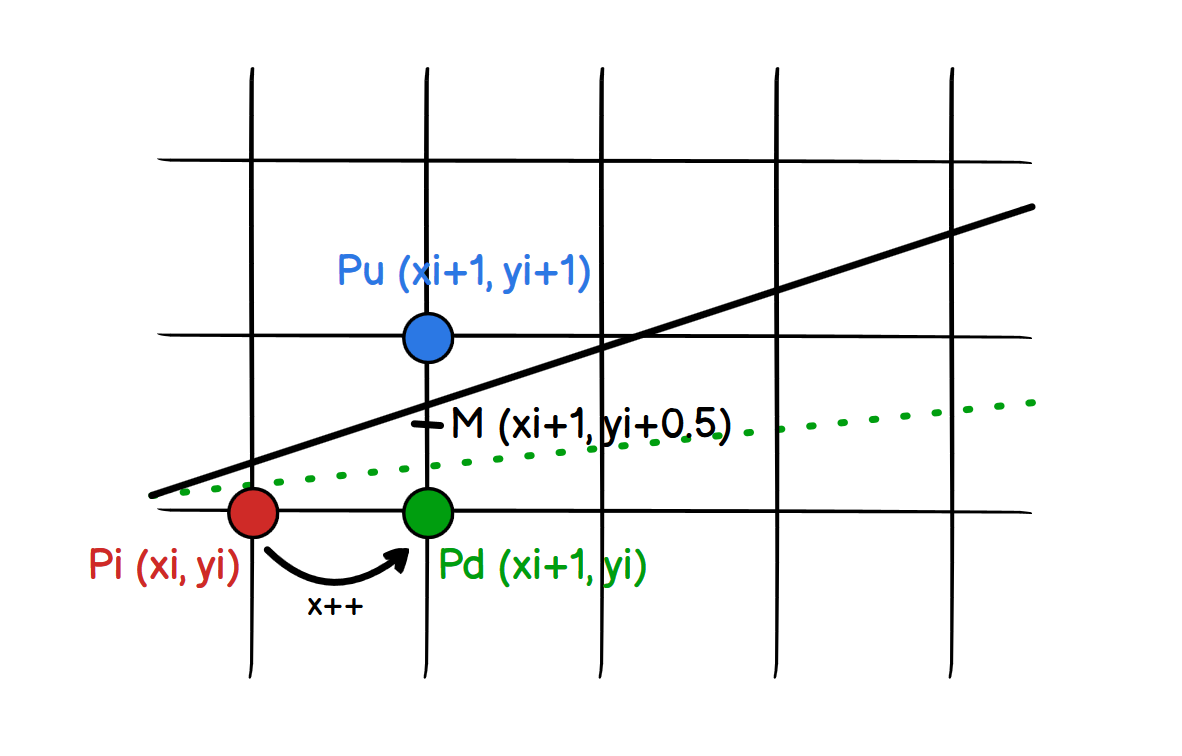
可以根据判别式决定下一个渲染的点是 PuP_uPu 还是 PdP_dPd:
d=F(xM,yM) d=F(x_M,y_M)
 软渲染两大直线算法详解
软渲染两大直线算法详解





 本文详细讲解了两种经典直线算法:DDA 和 Bresenham 算法,重点介绍了 Bresenham 算法的推导过程,包括中点 Bresenham、改进版和极简版。通过消除浮点数运算,Bresenham 算法成为现代最广泛应用的直线生成算法。
本文详细讲解了两种经典直线算法:DDA 和 Bresenham 算法,重点介绍了 Bresenham 算法的推导过程,包括中点 Bresenham、改进版和极简版。通过消除浮点数运算,Bresenham 算法成为现代最广泛应用的直线生成算法。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2074
2074

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








