2025年河南省暑期青少年程序设计能力提升集训DAY4图论基础-优快云博客

图的基本概念

以下是一些关于图的概念，记住总比不记要好，过于基础，可以跳过

图：图是一种由一组顶点和一组边组成的数据结构，记做，其中代表顶点集合代表边集合。

顶点：顶点是图的基本单位，也称为节点。

边：一条边是连接两个顶点的线段或弧。可以是无向的，也可以是有向的。一条边可以记做为。在无向图中，若存在一条，表示可以从点直接走到点，反之同理。但若在有向图中，存在一条边，表示可以从节点直接走向节点。

无向图：图中的边没有方向，即和是同一条边。

有向图：图中的边有方向，即和不是同一条边。

简单图：表示不含有重边（两个顶点之间的多条边）和自环（顶点到自身的边）的图。

多重图：允许有重边和自环的图。

边权：一般表示经过这一条边的代价（代价一般是由命题人定义的）。如下图，就是一个有向的简单图（通常来说，在有向图中边的方向用箭头来表示）：

度数：一个顶点的度是连接该顶点的边的数量。在有向图中，有入度和出度之分（具体例子见后文）。

路径：从一个顶点到另一个顶点的顶点序列，路径上的边没有重复。

回路：起点和终点相同的路径。

连通图：任意两个顶点之间都有路径相连的无向图。

强连通图：任意两个顶点之间都有路径相连的有向图。

图的表示方法

现在常用的遍历方法是邻接表和邻接矩阵，接下来将其分别说明

邻接矩阵

对于有向边E=(1,2)(2,3)(3,2),则邻接矩阵如图所示

0	1	2	3
1	1	1	0
2	0	1	1
3	0	1	1

代码示例：

int a[51][51];//建立表
for(int i=1;i<=50;i++){
    for(int j=1;j<=50;j++){
        a[i][j]=0;//初始化，（全局变量不用赋）
    }
}
a[1][2]=a[2][3]=a[3][2]=1;//赋值

邻接表

对于有向边E=(1,2)(2,3)(3,2),则邻接表如图所示

顶点数组: 
索引 | 顶点 | 相邻顶点链表 (头指针)
-----|------|---------------------------
  1  |  1  | -> [2] -> NULL
  2  |  2  | -> [3] -> NULL
  3  |  3  | -> [2] -> NULLd

代码示例：

vector<int> G[50]; // 建图。
G[1].push_back(2);
G[2].push_back(3);
G[3].push_back(2);
G[3].push_back(4);

对比下来

特性	邻接矩阵	邻接表
空间复杂度	O(V²)	O(V + E)
查边效率	O(1)（直接访问矩阵元素）	O(degree(V))（遍历链表）
添加边	O(1)	O(1)（链表头插）
遍历邻接点	O(V)（需扫描整行）	O(degree(V))
适用场景	稠密图（边数接近V²）	稀疏图

图的遍历

利用邻接矩阵，我们可以如此解决

int vis[105],map[105][105];
void dfs(int node){
    if(vis[node]) return ;
    vis[node]=1;
    cout<<node<<endl;
    for(int i=1;i<=n;i++)
    if (map[node][i]!=-0x7f7f7f7f) dfs(i);
    return ;
}

利用邻接表，我们可以如此解决

#include <vector>
vector<int> G[105];
int vis[105];
void dfs(int node){
    if(vis[node]) return ;
    vis[node]=1;
    cout<<node<<endl;
    for(auto to:G[node]) dfs(to);
    return ;
}

并查集

并查集（Disjoint Set Union, DSU）是一种用于高效处理动态连通性问题的数据结构，尤其适合管理元素分组和合并操作，对于具体原理这里不在说明，只给出应用及代码

赋值

int f[N];//f[x]表示x的父节点是谁
for(int i=1;i<=n;i++) f[i]=i;

查询

int getf(int x){return f[x]==x?x:getf(f[x]);}

优化

这里使用路径压缩，当然对于需要保留节点关系的题需要使用启发式合并

int getf(int x){ return f[x]==x?x:f[x]=getf(f[x]);}//更新父亲节点即可

下面是启发式合并

void merge(int x,int y){
    x=getf(x);y=getf(y);
    if(x==y) return;
    if(size[x]>size[y]) swap(x,y);
    f[x]=y;
    size[x]+=size[y];
}

合并

f[getf(x)]=getf(y);

拓扑排序

拓扑排序（Topological Sort）是针对有向无环图（DAG）的线性排序算法，其核心思想是满足图中所有边的方向性要求

下面进行解释

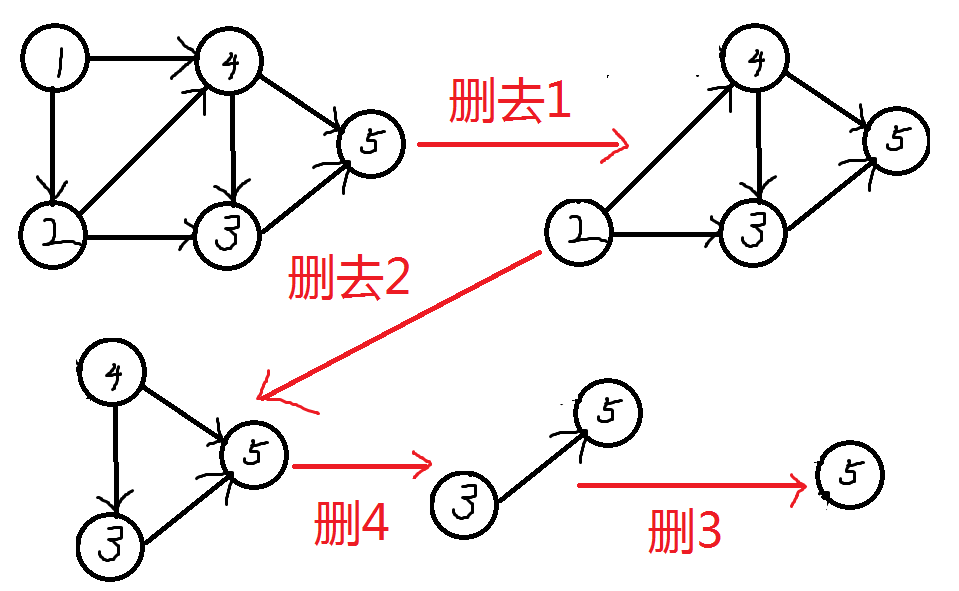
这张图解释的很详细了，找入度为0的删去，拓扑序为1 2 4 3 5

具体代码如下

void topsort(){
	queue<ll> q;
	for(int i=1;i<=n;i++) if(du[i]==0) q.push(i);
	while(!q.empty()){
		ll x=q.front(); q.pop();
		for(auto t:a[x]){
			ll y=t.first,v=t.second;
			du[y]--;
			if(c[x]>0) c[y]+=c[x]*v;
			if(!du[y]){
				c[y]-=u[y];
				q.push(y);
			}
		}
	}
}

（今天没什么时间，题就不说了。~~并不是我不想写，我没有水博客！~~）