2025年河南省暑期青少年程序设计能力提升集训DAY1（贪心+二分+倍增）

原创 已于 2025-07-04 19:07:23 修改 · 351 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #数据结构

于 2025-07-02 20:40:43 首次发布

内容

·贪心：

信息学竞赛的题目分为两类：最优解问题和方案数问题。  最优解问题是在所有可能的方案中，找出最优的方案，并记录答案。 为了保证最终结果最优，往往我们可以采用每步选择最优的“策略”，这就是贪心。

普及转提高时，贪心并不会很简单，有些时候结论是靠直觉的，而且还不一定正确，往往是贪心只能过样例，这时可以前几个数据暴力，后几个用贪心解决。

前几个题目正常贪，如 D - AtCoDeer and Rock-Paper (AI)；最大整数 等均为排序找规律，再往后就是微扰排序了，如 Cow Acrobats，注意找规律贪，这里点一下「CCO 2015」饥饿的狐狸 这道，恶心人；

然后是中位数类型的贪心，经典例题货仓选址，其他的如「一本通 1.1 练习 6」糖果传递，数学分析后本质也是货仓选址；

最后是堆（优先队列），自动排序，很好用，如D - Powerful Discount Tickets，用优先队列能更好的辅助贪心策略

（注：对顶堆没听太懂，回去可以复习一下）

·二分：

二分，也叫折半，其本质还是分治。 二分从应用上分为二分查找和二分答案

二分与倍增是互逆的两种思想； 二分是将范围缩小的过程； 倍增是将范围扩大的过程。 无论二分还是倍增，都是二进制思想的应用。

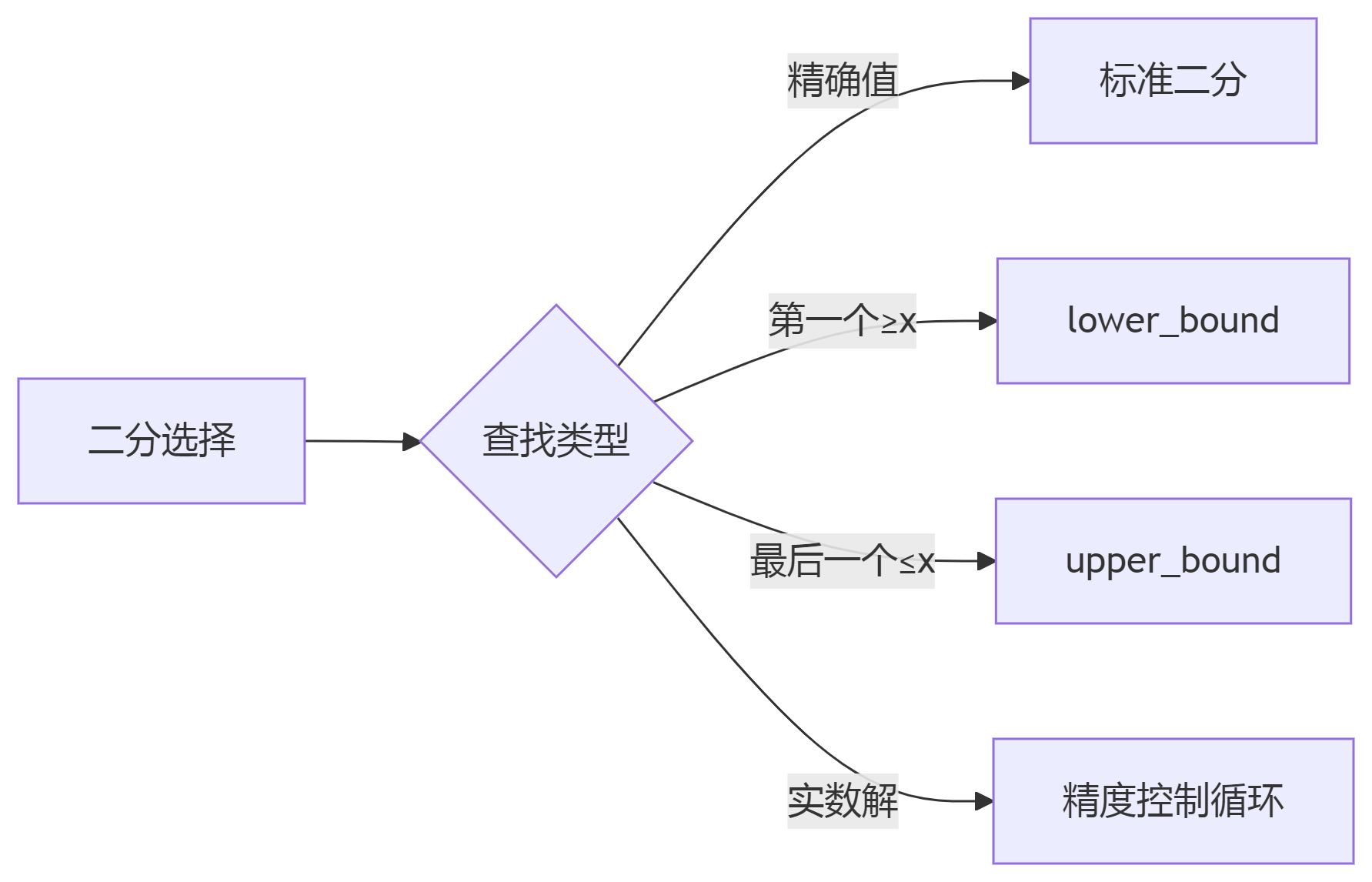
经典查找类型的模板：

这里重点说一下二分查找，重点是如何快速检查答案，模板如下：

bool check(ll x){
	···check···
}

while(l+1<r){
	ll mid=(l+r)/2;
	if(check(mid)) l or r=mid;//注意最小值往左走，最大值往右走
	else r or l=mid;
}
if(check(l)) cout<<l;
else cout<<r;

·倍增：

倍增是根据已经得到的信息，将考虑的范围扩大一倍，从而加速操作的一种思想 使用了倍增思想的算法： 快速幂。 基于ST表的RMQ算法 树上倍增找LCA FFT、后缀数组等高级算法

重点为ST表，只能维护定值数组，不可修改，主要有维护区间最大/小值，区间最大公约数等，下面为模板：

void pre(){
	Logn[1]=0;
	Logn[2]=1;
	af(i,3,N){
		Logn[i]=Logn[i/2]+1;
	}
}

af(j,1,21){
	af(i,1,n-(1<<j)+1){ //i+(1<<j)-1<=n   =>   i<=n-(1<<j)+1 
		a[i][j]=max(a[i][j-1],a[i+(1<<(j-1))][j-1]);
	}
}
af(i,1,m){
	ll x=read(),y=read();
	ll s=Logn[y-x+1];
	printf("%lld\n",max(a[x][s],a[y-(1<<s)+1][s]));
}

总结

注意多练

题解

（这里省略一些较简单的）

D - AtCoDeer and Rock-Paper (AI)：多出布即可，这里有一种简单写法

#include <bits/stdc++.h>
#define ll long long
#define af(a,b,c) for(ll a=b;a<=c;a++)
#define bf(a,b,c) for(ll a=b;a>=c;a--)
#define pll pair<ll,ll>
using namespace std;
void fre(){ freopen("apb.in","r",stdin);freopen("apb.out","w",stdout);}
ll lowbit(ll x){ return x&(-x);}
inline ll read(){
	ll _s=0,_w=1; char _ch=getchar();
	while(_ch<'0'||_ch>'9'){ if(_ch=='-') _w=-1; _ch=getchar();}
	while(_ch>='0'&&_ch<='9'){ _s=_s*10+_ch-'0'; _ch=getchar();}
	return _s*_w;
}


const ll N=1e6+10;
string s[N];
ll sum_p=0;


signed main(){
//	fre();
	string s;
	cin>>s;
	af(i,0,s.size()-1){
		if(s[i]=='p'){
			sum_p++;
		}
	}
	cout<<s.size()/2-sum_p;
}

最大整数：特殊排序即可

#include <bits/stdc++.h>
#define ll long long
#define af(a,b,c) for(ll a=b;a<=c;a++)
#define bf(a,b,c) for(ll a=b;a>=c;a--)
#define pll pair<ll,ll>
using namespace std;
void fre(){ freopen("apb.in","r",stdin);freopen("apb.out","w",stdout);}
ll lowbit(ll x){ return x&(-x);}
inline ll read(){
	ll _s=0,_w=1; char _ch=getchar();
	while(_ch<'0'||_ch>'9'){ if(_ch=='-') _w=-1; _ch=getchar();}
	while(_ch>='0'&&_ch<='9'){ _s=_s*10+_ch-'0'; _ch=getchar();}
	return _s*_w;
}


const ll N=1e6+10;
string s[N];


bool cmp(string x1,string x2){
	return x1+x2>x2+x1;
}


signed main(){
//	fre();
	ll n;
	n=read();
	af(i,1,n) cin>>s[i];
	sort(s+1,s+n+1,cmp);
	af(i,1,n) cout<<s[i];
}



​​​​​​删数问题：特殊判断，重点为数位性质

#include <bits/stdc++.h>
#define ll long long
#define af(a,b,c) for(ll a=b;a<=c;a++)
#define bf(a,b,c) for(ll a=b;a>=c;a--)
#define pll pair<ll,ll>
using namespace std;
void fre(){ freopen("keks.in","r",stdin);freopen("keks.out","w",stdout);}
ll lowbit(ll x){ return x&(-x);}
inline ll read(){
	ll _s=0,_w=1; char _ch=getchar();
	while(_ch<'0'||_ch>'9'){ if(_ch=='-') _w=-1; _ch=getchar();}
	while(_ch>='0'&&_ch<='9'){ _s=_s*10+_ch-'0'; _ch=getchar();}
	return _s*_w;
}


const ll N=1e6+10;
ll n,k;
stack<ll> a;


signed main(){
	fre();
	n=read(); k=read();
	string s; cin>>s;
	ll i=0;
	while(i<n){
		while(!a.empty()&&k&&a.top()<s[i]-'0'){
			a.pop();
			k--;
		}
		a.push(s[i]-'0');
		i++;
	}
	string ss="";
	ll len=a.size();
	af(i,1,len){
		ss+=a.top()+'0';
		a.pop();
	}
	reverse(ss.begin(),ss.end());
	cout<<ss;
}

最恶心的一道「CCO 2015」饥饿的狐狸（写了1个多小时）

最小值找规律，最大值两个都要算一下，选最优，思路其实不难，只是代码细节较多

#include <bits/stdc++.h>
#define ll long long
#define af(a,b,c) for(ll a=b;a<=c;a++)
#define bf(a,b,c) for(ll a=b;a>=c;a--)
#define pll pair<ll,ll>
using namespace std;
void fre(){ freopen("keks.in","r",stdin);freopen("keks.out","w",stdout);}
ll lowbit(ll x){ return x&(-x);}
inline ll read(){
	ll _s=0,_w=1; char _ch=getchar();
	while(_ch<'0'||_ch>'9'){ if(_ch=='-') _w=-1; _ch=getchar();}
	while(_ch>='0'&&_ch<='9'){ _s=_s*10+_ch-'0'; _ch=getchar();}
	return _s*_w;
}


const ll N=1e6+10;
ll n,w;
ll a[N];


signed main(){
//	fre();
	n=read(); w=read();
	af(i,1,n) a[i]=read();
	sort(a+1,a+n+1);
	if(w<a[1]) cout<<a[n]-w<<' ';
	else if(w>a[n]) cout<<w-a[1]<<' ';
	else cout<<a[n]-a[1]<<' ';
	
	ll lastt=w,ansl=0,ansr=0;
	ansl+=abs(w-a[1]);
	lastt=a[1];
	ll l=2,r=n;
	af(i,2,n){
		if(!(i%2)){
			ansl+=max(abs(lastt-a[r]),abs(w-a[r]));
			lastt=a[r]; r--;
		}else{
			ansl+=max(abs(lastt-a[l]),abs(w-a[l]));
			lastt=a[l]; l++;
		}
	}
	ansr+=abs(w-a[n]);
	lastt=a[n];
	l=1,r=n-1;
	af(i,2,n){
		if(i%2){
			ansr+=max(abs(lastt-a[r]),abs(w-a[r]));
			lastt=a[r]; r--;
		}else{
			ansr+=max(abs(lastt-a[l]),abs(w-a[l]));
			lastt=a[l]; l++;
		}
	}
	cout<<max(ansl,ansr);
}


 



糖果传递：这个要写方程找规律

#include <bits/stdc++.h>
#define ll long long
#define af(a,b,c) for(ll a=b;a<=c;a++)
#define bf(a,b,c) for(ll a=b;a>=c;a--)
#define pll pair<ll,ll>
using namespace std;
void fre(){ freopen("keks.in","r",stdin);freopen("keks.out","w",stdout);}
ll lowbit(ll x){ return x&(-x);}
inline ll read(){
	ll _s=0,_w=1; char _ch=getchar();
	while(_ch<'0'||_ch>'9'){ if(_ch=='-') _w=-1; _ch=getchar();}
	while(_ch>='0'&&_ch<='9'){ _s=_s*10+_ch-'0'; _ch=getchar();}
	return _s*_w;
}


const ll N=1e6+10;
ll n,sum=0,ans;
ll a[N],c[N];


signed main(){
//	fre();
	n=read();
	af(i,1,n) a[i]=read(),sum+=a[i];
	ll endd=sum/n;
	af(i,1,n) c[i]=a[i]+c[i-1]-endd;
	sort(c+1,c+n+1);
	for(ll l=1,r=n;l<r;l++,r--) ans+=c[r]-c[l];
	cout<<ans;
}

题太多了，以后有时间再补吧

子 之
关注
评论 1
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值