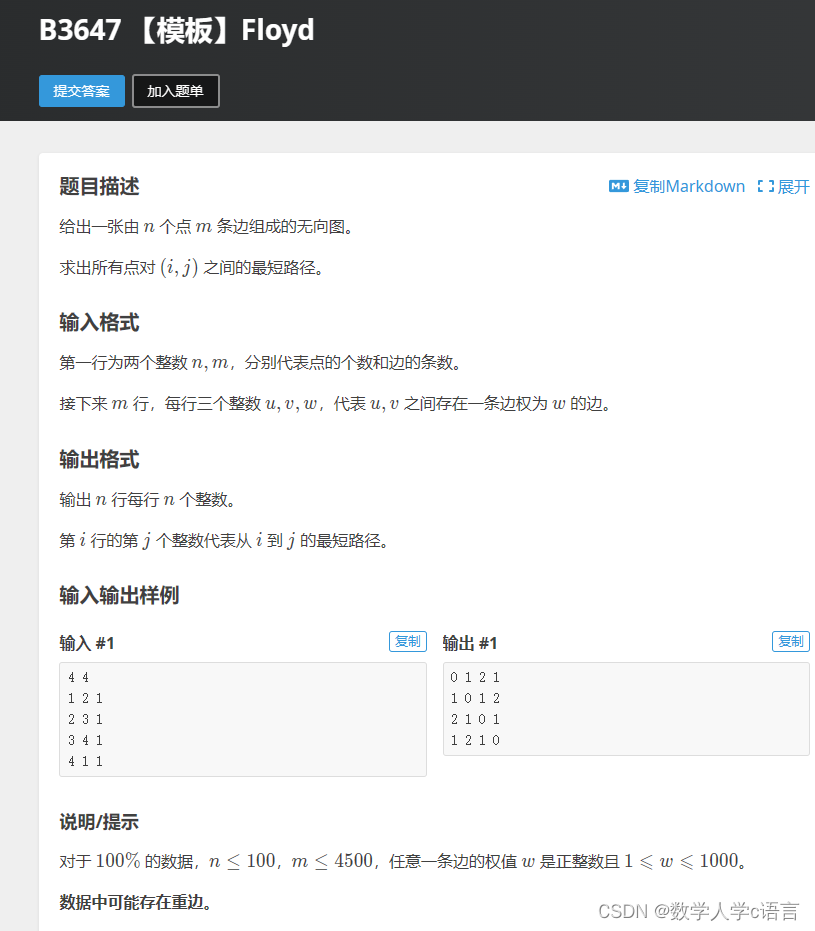
先上代码:
n, m = map(int, input().split())
edge = [ [float('inf')]*n for _ in range(n)]
for i in range(m):
u, v, w = map(int, input().split())
edge[u-1][v-1] = min(edge[u-1][v-1], w)
edge[v-1][u-1] = min(edge[v-1][u-1], w)
for i in range(n):
edge[i][i] = 0
for k in range(n):
for i in range(n):
for j in range(n):
edge[i][j] = min(edge[i][j], edge[i][k] + edge[k][j])
for i in range(n):
for j in range(n):
print(edge[i][j], end=' ')
print()
floyd算法知道长什么样,就是三层for循环呗,但是理解起来不是很简单。
为什么要进行三层循环,因为三层循环之后,从节点i到节点j的所有路径都遍历了一遍,找到最小值。
我们节点i到节点j的最短路径(现在节点i和节点j是某两个节点,已经固定)考虑算法首先初始化,
如果i和j直接存在路径,那么edge[i][j] = w。或者不存在路径,edge[i][j]=inf。
现在开始第一层循环,k = 1:
不考虑i==k和j==k的情况(毕竟如果相等,那么edge[i][j]任然等于w或者inf),现在i!=k and j!=k,那么edge[i][j] = min(edge[i][j], edge[i][k] + edge[k][j]),取值为节点i到j的情况,和节点i到k到j的情况,这里我就简写,i-j 和 i-1-j
k = 2:
edge[i][j] = min(edge[i][j], edge[i][2] + edge[2][j]),这里面存在 i-j,和i-2-j的情况,只有这两个吗???第一重循环中,已经计算了任意两个节点以节点1为桥的情况,那么现在全部情况应该是:i-j, i-1-j, i-2-j, i-1-2-j, i-2-1-j 这五种情况。
k = ....
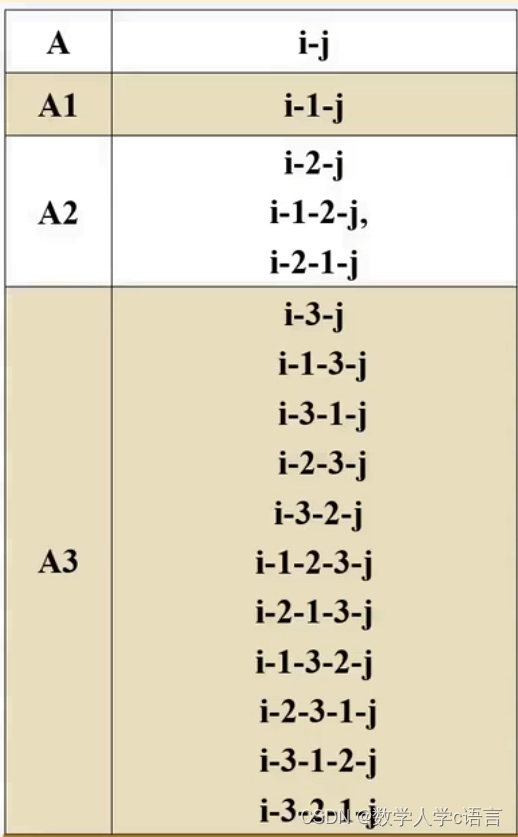
k取完1-n之后,edge[i][j] 表示从节点i到节点j的所有可能存在的路径的最小值。
所以Floyd能奏效。




















 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








