24.二叉树的层次遍历(UVa122)

问题：

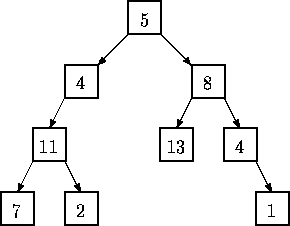
树状结构在计算机科学的许多领域中都相当重要。本问题牵涉到建立树及走访树。给你一二叉树，你的任务是写一个程序来打印依「阶层（level-order）」走访的结果。在本问题中，二叉树的每个节点含有一个正整数，并且节点的数目最少1个，最多256个。在阶层走访中，依阶层从低到高，同阶层从左到右的次序来打印。例如以下的二叉树阶层走访的结果为：5，4，8，11，13，4，7，2，1

输入：
(11,LL) (7,LLL) (8,R) (5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()

输出：
5 4 8 11 13 4 7 2 1

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;

//树结点 
struct Node {
	int v;
	Node* left, *right;
	int have_value;
	Node() :have_value(false), left(NULL), right(NULL) {};
};

Node* root;//根节点

Node* newnode() {
	return new Node(); //返回一个新结点 
}

bool failed;

void addnode(int v, char* s) {//添加新结点 
	int n = strlen(s);
	Node* u = root; // 每一个节点都是相对根节点的位置，所以每次从根节点开始找
	for (int i = 0; i < n; i++)//找到要加入的位置 
	{
		if (s[i] == 'L') { 
			if (u->left == NULL) u->left = newnode(); // 如果之前没有建立左子树，现在建立左子树
			u = u->left; // LL,树的往下延伸
		}
		else if (s[i] == 'R') {
			if (u->right == NULL) u->right = newnode();
			u = u->right;
		}
	}
	if (u->have_value) failed = true;//要赋值的节点，是否已经被赋值过；
	u->v = v;// 给该节点赋节点值
	u->have_value = true; //标记它已经被赋值过
}

void freetree(Node* u) { //释放内存 
	if (u == NULL) return; // return NULL;
	freetree(u->left); //先删除子节点
	freetree(u->right);
	delete u;
}

char s[1005];
bool read_input() {
	failed = false;
	freetree(root);
	root = newnode();
	while (true) {
		if (scanf("%s", s) != 1) return false; //(11,LL)
		if (!strcmp(s, "()")) break; // ()表示结束
		int v; 
		sscanf(&s[1], "%d", &v); // &s[1]是指针，从这个位置开始，取整数给v，v = 11
		addnode(v, strchr(s, ',') + 1); // 查找到“，”，并将后面的位置传给插入节点函数
	}
	return true;
}

bool bfs(vector<int>& ans) { //按层次遍历这棵树
	queue<Node*> q; //队列
	ans.clear();
	q.push(root); // 初始化只有一个根节点
	while (!q.empty()) {
		Node *u = q.front(); q.pop(); // 记录首元素，并删除
		if (!u->have_value) return false; // 有节点没有被赋值过，表明输入有误
		ans.push_back(u->v); // 这个节点的值增加到输出序列
		if (u->left != NULL)    q.push(u->left); //将左子节点（如果有）放入队列
		if (u->right != NULL) q.push(u->right); //将右子节点（如果有）放入队列
	} // 只要保证每一次先遍历父节点，在将左右子节点放入队列依次处理，整体就不会错
	return true;
}

int main(int argc, char *argv[])
{
	vector<int> ans; // 答案
	while (read_input()) { 
		if (!bfs(ans)) failed = 1; //层次遍历这棵树不成功
		if (failed) printf("not complete\n");
		else {
			for (int i = 0; i < ans.size(); i++)
			{
				if (i != 0) cout << " ";
				cout << ans[i];
			}
			cout << endl;
		}
	}
	return 0;
}