线性回归与高级回归模型实践：带交叉验证（CV）的多元套索回归

带交叉验证（CV）的多元套索回归

学习目标

本课程将探讨高维回归中的常见问题，如过拟合和R平方拟合的误导性，并介绍LASSO正则化作为一种有效的解决方案，通过具体示例演示如何使用LASSO正则化和交叉验证构建更健壮的元模型。

学习内容

1 基于随机采样的具有 DOE 的多元回归元模型

输入变量空间建议使用随机采样来构建。随机采样可以是多种形式，例如简单随机抽样、拉丁超立方体采样等。这种方法的优点是可以更广泛地覆盖输入空间，尤其是对于高维空间，可以避免经典阶乘设计（DOE，Design of Experiments）的一些局限性。
经典阶乘 DOE 通常是一种结构化的实验设计方法，它按照因素水平的组合来安排实验或数据点，对于低维空间可能比较有效，但在高维空间会导致样本点数量呈指数级增长，变得不切实际或难以处理。而随机采样可以根据所需样本数量在整个输入空间中随机选取样本点，更加灵活，适用于高维问题。
线性拟合通常不足以捕捉输入和输出之间的复杂关系。对于许多实际问题，线性关系过于简单，无法很好地描述数据中的模式，导致模型的拟合效果不佳，无法充分解释变量之间的关系。
高阶多项式拟合虽然能够更灵活地拟合数据，但其缺点是容易导致过拟合。过拟合意味着模型过度学习了训练数据中的噪声和异常，而不是真实的数据关系，会导致模型在训练数据上表现很好，但在新的、未见过的数据上表现很差。它会学习到输入和输出之间一些虚假和有缺陷的关系，使模型的泛化能力下降。

1.1 配置运行环境

%pip install scikit-learn==1.1.3

# 导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

在搭建好环境之后，我们将生成随机特征向量，该随机特征向量的生成方式相当于在 Optislang 中所完成的拉丁超立方采样。

X=np.array(10*np.random.randn(37,5))
df=pd.DataFrame(X,columns=['Feature'+str(l) for l in range(1,6)])
df.head()

这里使用 df.hist() 方法绘制直方图展示出输入特征的随机分布。

for i in df.columns:
    df.plot.scatter(i,'y', edgecolors=(0,0,0),s=50,c='g',grid=True)

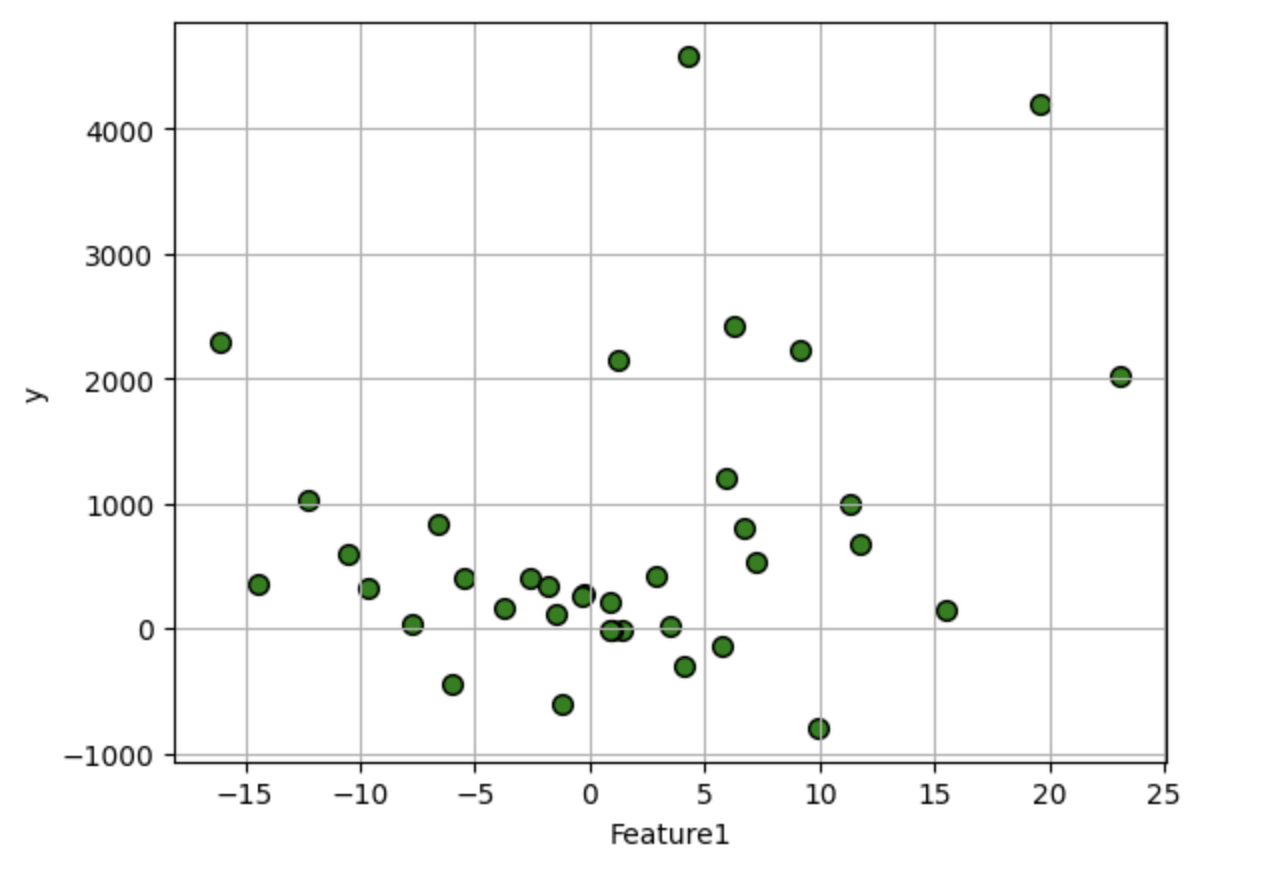
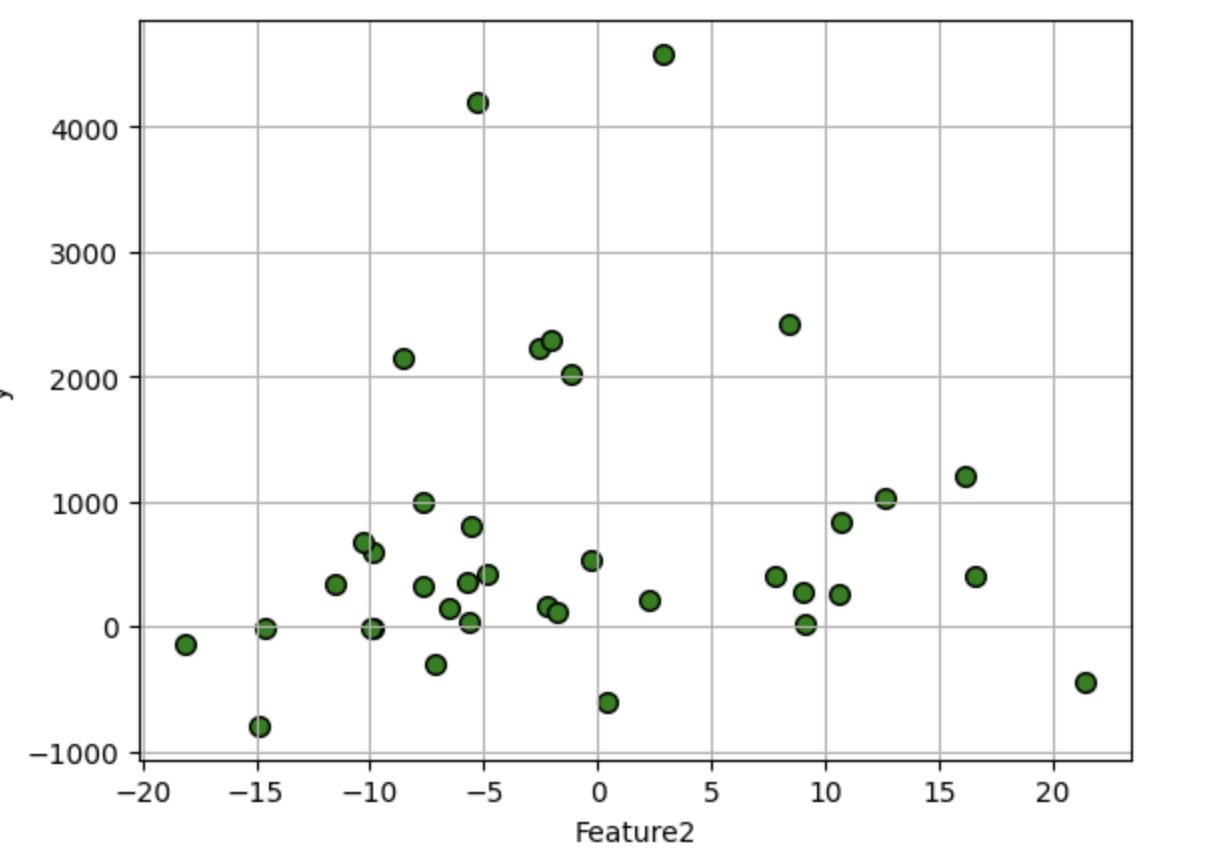
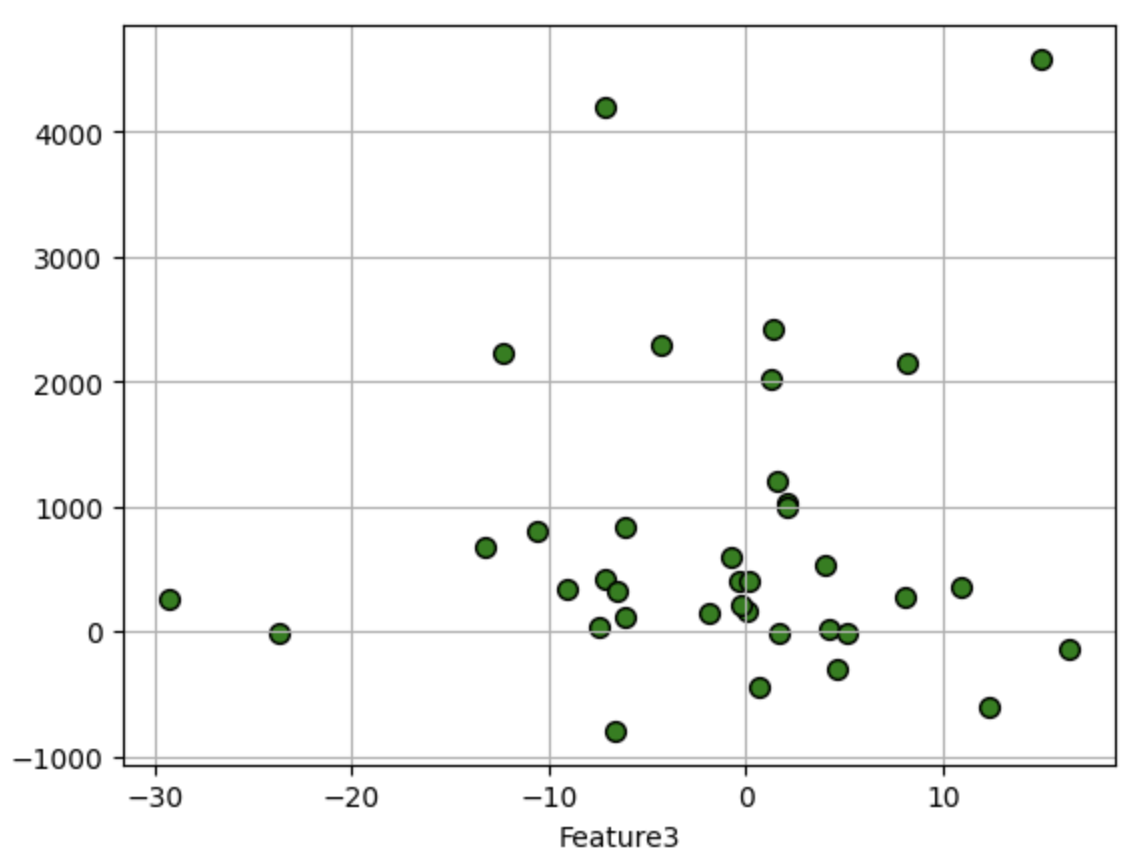
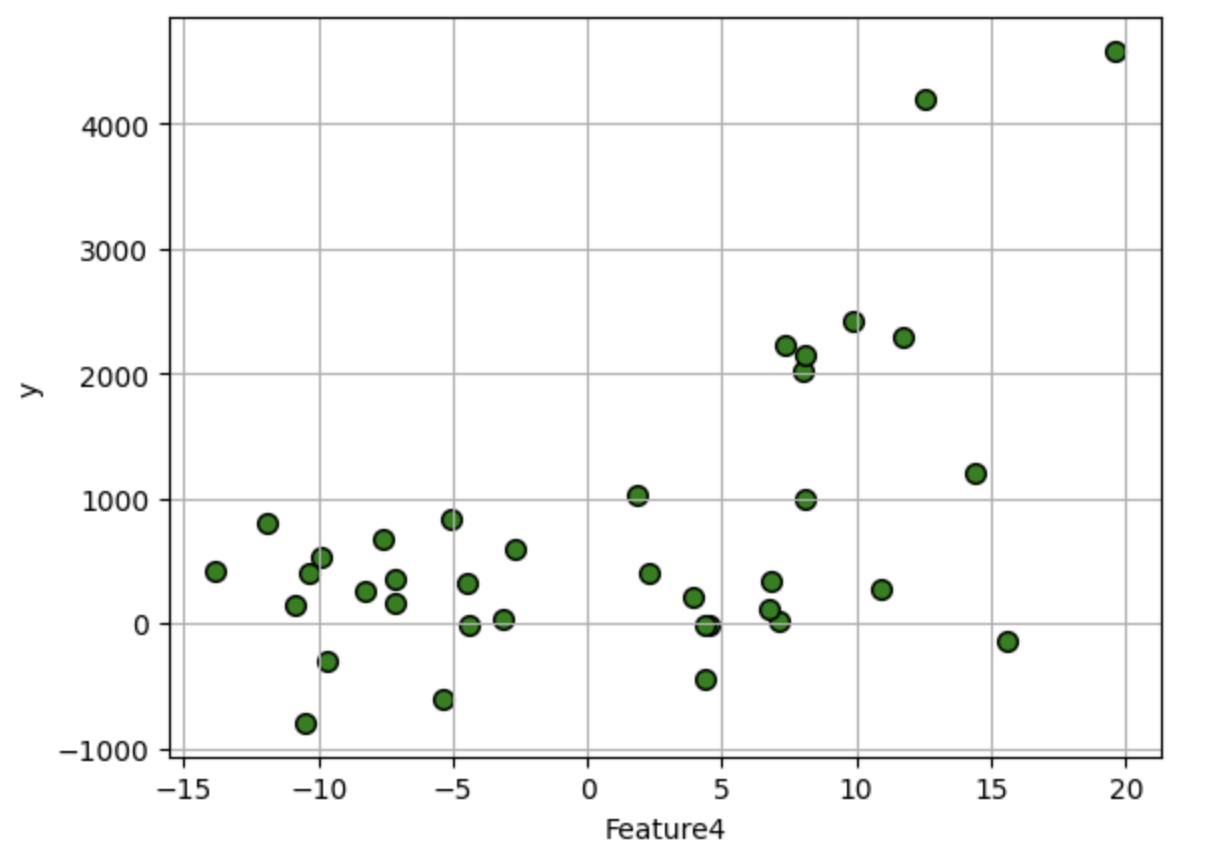
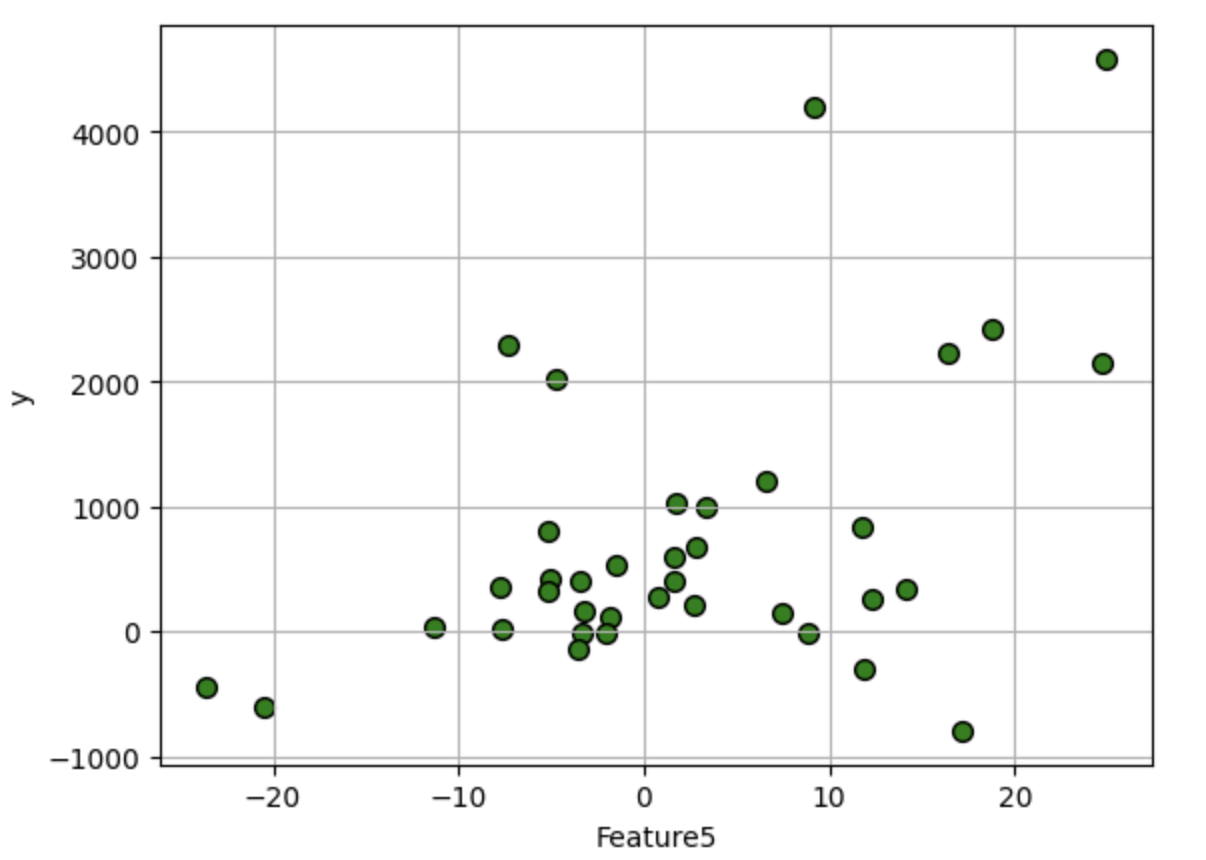
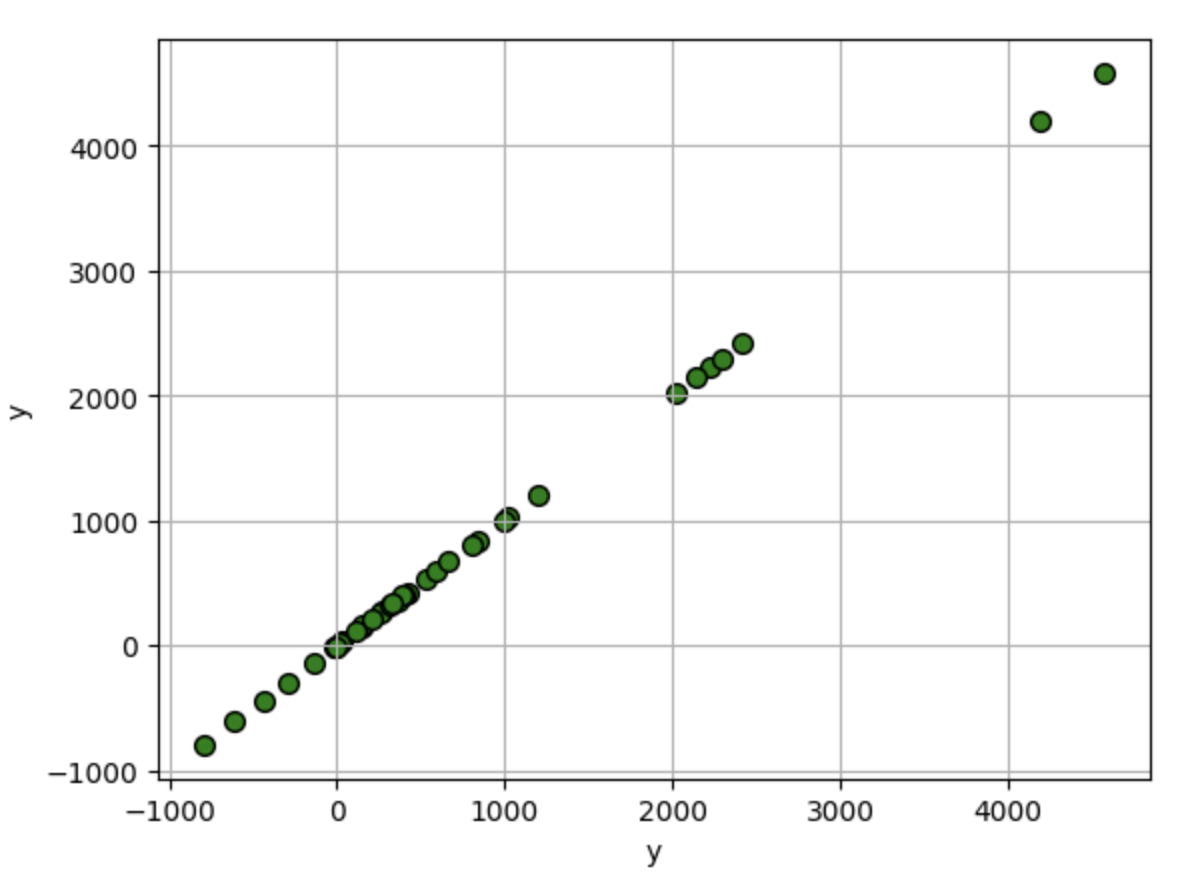
在这里插入图片描述

1.2 标准线性回归分析

下面我们创建实例化对象，并使用 LinearRegression 进行标准线性回归拟合。

from sklearn.linear_model import LinearRegression
# 创建了一个线性回归模型对象 linear_model
linear_model = LinearRegression()
X_linear=df.drop('y',axis=1)
y_linear=df['y']
linear_model.fit(X_linear,y_linear)
# 使用之前创建并训练好的线性回归模型 linear_model 对特征矩阵 X_linear 进行预测。
y_pred_linear = linear_model.predict(X_linear)
RMSE_linear = np.sqrt(np.sum(np.square(y_pred_linear-y_linear)))
# 打印出线性模型的均方根误差（Root-mean-square error，RMSE）
print("Root-mean-square error of linear model:",RMSE_linear)
coeff_linear = pd.DataFrame(linear_model.coef_,index=df.drop('y',axis=1).columns, columns=[