神经网络中的几个函数解释

1.step阶跃函数：

在神经网络领域，Step（阶跃函数） 是一种基础且简单的激活函数，核心作用是为神经元引入非线性判断能力，其工作逻辑和特点如下：

1. 核心定义
   阶跃函数以一个预设的“阈值”为界，对输入信号进行二元化输出：当输入值大于等于阈值时，输出固定的“激活值”（通常为1）；当输入值小于阈值时，输出“抑制值”（通常为0）。
   典型数学表达式（以阈值=0为例）：
   $$f(x)=\{\begin{array}{ll}1& (x\ge 0)\\ 0& (x<0)\end{array}$$

2. 核心作用
   早期用于模拟生物神经元的“兴奋/抑制”状态——只有当输入信号（经权重叠加后）达到一定强度，神经元才会被激活并传递信号，否则保持沉默，是构建简单感知机（如二分类任务）的基础组件。

3. 局限性
   由于输出仅为0或1的离散值，阶跃函数存在明显缺陷：

   • 梯度为0：除阈值点外，函数处处不可导（或导数为0），无法通过反向传播优化神经网络参数，因此不适用于深度网络训练；
   • 输出离散：无法传递输入信号的“强度差异”（例如输入=1和输入=10的输出相同），表达能力弱。

4. 应用场景
   目前已很少用于深度学习模型，但在入门教学中常用于理解“激活函数的基本逻辑”，或在极简的二分类场景（如简单逻辑判断）中偶尔使用，实际深度网络中多被ReLU、Sigmoid等更灵活的激活函数替代。

2.Sigmoid函数

Sigmoid是一种常用的神经网络激活函数，数学表达式为：
( \sigma(x) = \frac{1}{1 + e^{-x}} )

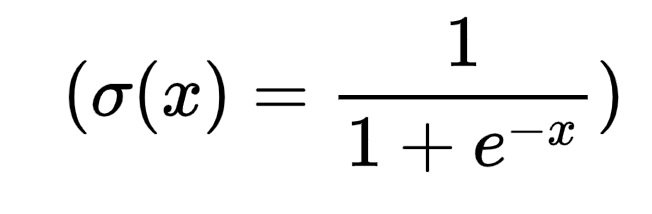
它的主要特点包括：

• 输出范围在(0, 1)之间，能将任意实数映射到这个区间，适合用于二分类问题的输出层，表示概率
• 具有平滑的梯度特性，便于反向传播计算
• 是单调递增函数，保持输入的排序关系

但Sigmoid也存在局限性：

• 容易出现梯度消失问题，当输入值过大或过小时，梯度接近0，影响深层网络的训练
• 输出不是以0为中心，可能导致权重更新效率降低
• 计算涉及指数运算，相对其他激活函数（如ReLU）计算成本较高

在现代深度学习中，Sigmoid更多用于特定场景（如输出层的二分类概率），隐藏层则常被ReLU及其变体替代。

3.双曲正切函数Tanh

Tanh（双曲正切函数）是神经网络中常用的激活函数之一，其数学表达式为：
tanh(x) = (eˣ - e⁻ˣ) / (eˣ + e⁻ˣ)

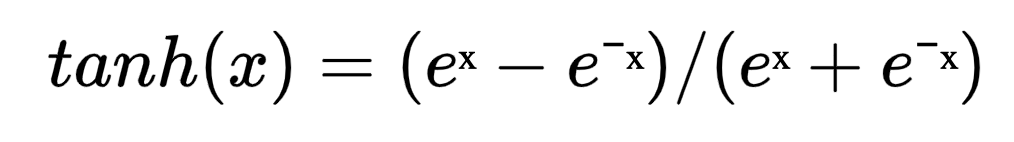
它的主要特点包括：

1. 输出范围：将输入值映射到[-1, 1]区间，相比Sigmoid函数（输出[0,1]）更接近零均值，有助于缓解训练过程中的梯度消失问题。
2. 非线性特性：能引入非线性变换，使神经网络可学习复杂模式。
3. 对称性：关于原点对称，当输入为正时输出为正，输入为负时输出为负，适合需要区分正负特征的场景。

在应用中，Tanh常被用于隐藏层，但计算成本略高于ReLU，且仍存在一定的梯度消失问题，因此在深层网络中使用较少。

4.修正线性修正线性单元ReLU

ReLU（Rectified Linear Unit，修正线性修正线性单元）是深度学习中常用的激活函数，其数学表达式为：
$f(x)=\max (0,x)$

即当输入$x$为正数时，输出直接直接原输入值；当$x$为负数时，输出0。

特点：

1. 计算高效：仅需简单的阈值判断，比sigmoid、tanh等函数的指数运算更快，能加速模型训练。
2. 缓解梯度消失：在正区间导数恒为1，避免了深层网络中梯度随层数增加而急剧衰减的问题。
3. 稀疏激活：负数输入会被置为0，使部分神经元"失活"，增强模型泛化能力，减少过拟合风险。

不足：存在"死亡ReLU"问题——若神经元长期接收负输入，可能永久失活（梯度为0，无法更新参数）。后续变体如Leaky ReLU、Parametric ReLU等通过允许小的负输出缓解了这一问题。

ReLU广泛应用于卷积神经网络（CNN）、循环神经网络（RNN）等模型的隐藏层，是现代深度学习的基础组件之一。

5.带泄露的修正线性单元LReLU

LReLU（带泄露的修正线性单元）是ReLU激活函数的变体，主要用于解决ReLU可能出现的“神经元失活”问题。

其函数表达式为：当输入x ≥ 0时，输出x；当x < 0时，输出一个很小的负值（通常是0.01x）。

相比ReLU将所有负值直接置为0，LReLU允许小幅度的负信号通过，这有助于维持神经元的活性，避免因某些神经元长期输出为0而失去学习能力。这种特性在一定程度上提升了模型的泛化能力，尤其在训练较深的神经网络时可能带来更好的效果。

在PyTorch中，可以通过nn.LeakyReLU()来实现该激活函数，使用时可通过参数调整负斜率的大小。

6.softmax函数

Softmax是深度学习中常用的激活函数，主要用于多分类问题的输出层。

它的核心作用是将神经网络输出的多个实数（通常称为logits）转换为一组概率值，这些概率值满足两个特性：

1. 每个值都在0到1之间
2. 所有值的总和为1

数学上，对于输入向量中的每个元素( z_i )，Softmax的计算方式为：
( $\sigma (z{)}_i=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$ )

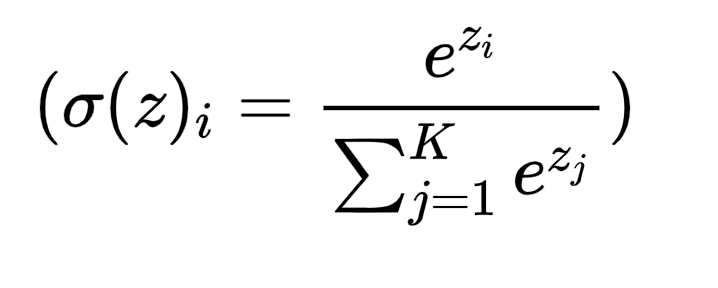
其中K是类别总数。

这种转换使得输出可以被解释为每个类别的预测概率，便于后续计算交叉熵损失等。在实际应用中，它能突出输入向量中的较大值，同时抑制较小值，让模型更明确地倾向于某个类别。