SciPy科学计算与应用：SciPy统计分析入门-掌握scipy.stats进行数据统计与应用

原创已于 2025-08-27 16:24:00 修改 · 295 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#scipy

于 2025-08-27 10:17:15 首次发布

SciPy统计分析实战：从基础到应用

学习目标

通过本课程，学员将掌握使用SciPy的统计模块（scipy.stats）进行数据的统计分析。同时通过学习，学员将能够理解并应用概率分布、假设检验和回归分析等统计方法，解决实际问题。

学习内容

1 SciPy统计分析实战：从基础到应用

1.1 概率分布

概率分布是统计学中的一个基本概念，它描述了随机变量取值的概率。在SciPy中，scipy.stats模块提供了大量的概率分布函数，可以用来生成随机数、计算概率密度函数（PDF）、累积分布函数（CDF）等。

1.1.1 常见的概率分布

在统计分析中，经常遇到的几种概率分布包括正态分布、二项分布、泊松分布等。每种分布都有其特定的应用场景和参数。

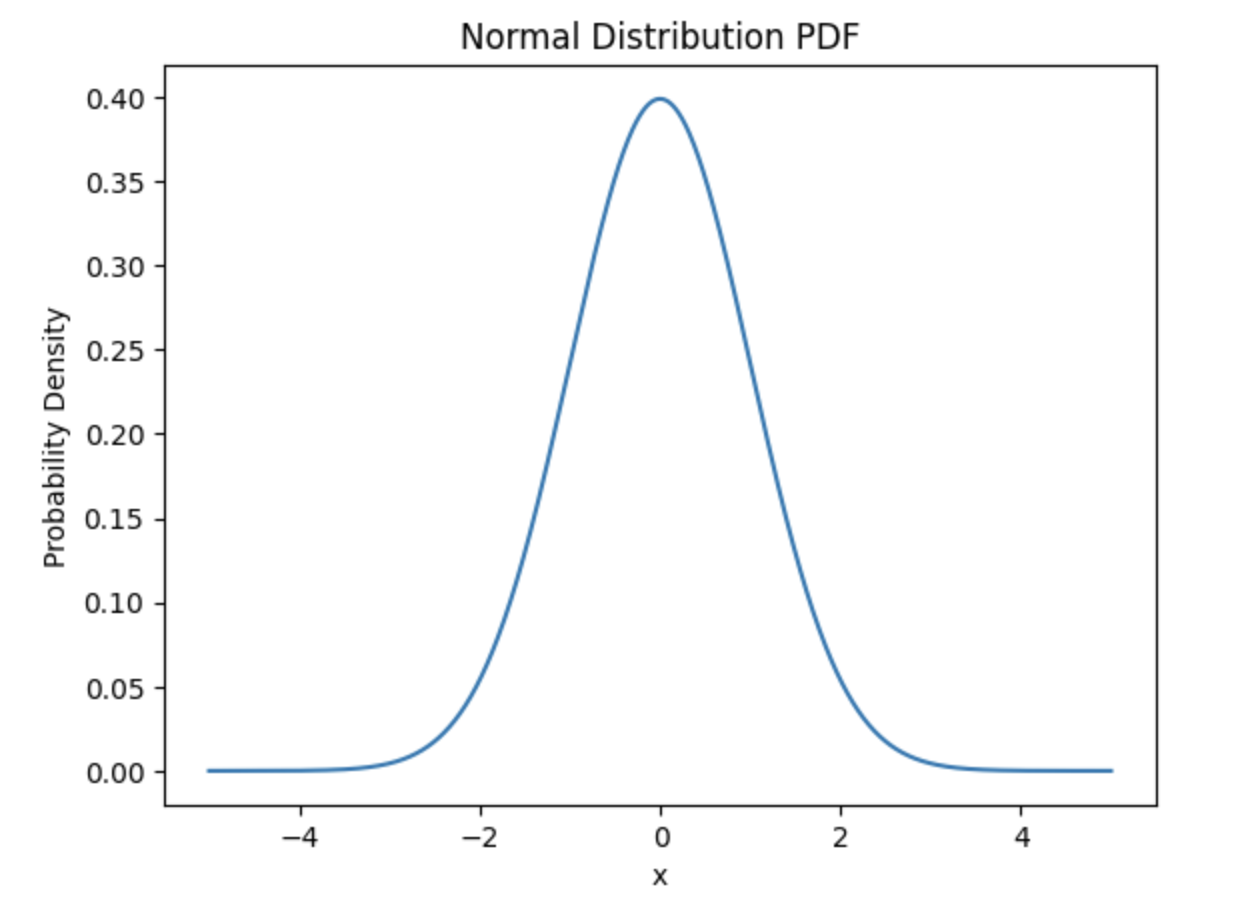
正态分布：正态分布是最常见的一种连续概率分布，其概率密度函数呈钟形曲线。在SciPy中，可以使用norm对象来表示正态分布。正态分布有两个参数：均值（loc）和标准差（scale）。

from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np

# 定义正态分布的参数
mean = 0
std_dev = 1

# 生成正态分布的概率密度函数
x = np.linspace(-5, 5, 1000)
y = norm.pdf(x, loc=mean, scale=std_dev)

# 绘制正态分布的PDF
plt.plot(x, y)
plt.title('Normal Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

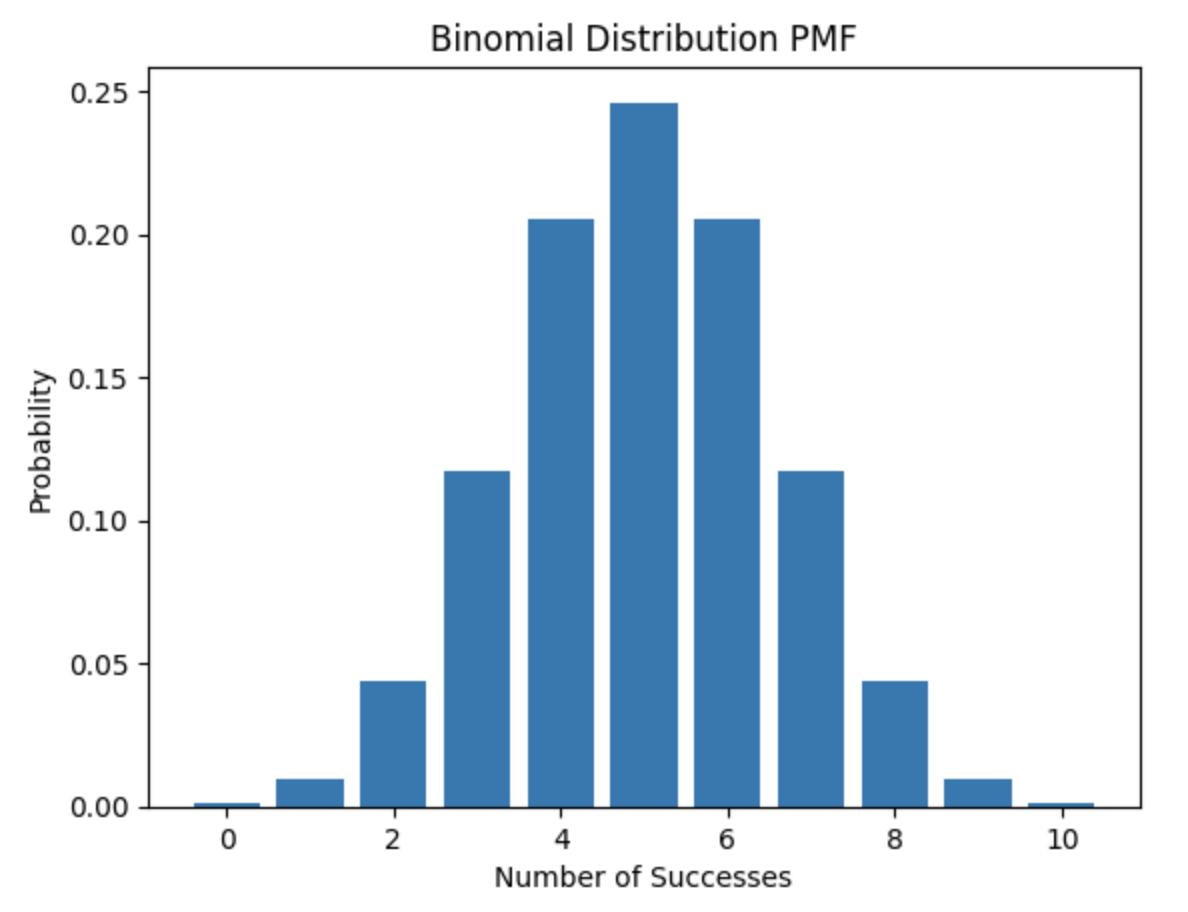
在这里插入图片描述

二项分布：二项分布是一种离散概率分布，用于描述在固定次数的独立伯努利试验中成功次数的概率。在SciPy中，可以使用binom对象来表示二项分布。二项分布有两个参数：试验次数（n）和每次试验成功的概率（p）。
在这里插入代码片：

from scipy.stats import binom

# 定义二项分布的参数
n = 10
p = 0.5

# 生成二项分布的概率质量函数
x = np.arange(0, n+1)
y = binom.pmf(x, n, p)

# 绘制二项分布的PMF
plt.bar(x, y)
plt.title('Binomial Distribution PMF')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.show()

在这里插入图片描述

泊松分布：泊松分布是一种离散概率分布，用于描述单位时间内事件发生的次数。在SciPy中，可以使用poisson对象来表示泊松分布。泊松分布有一个参数：事件发生的平均次数（mu）。

from scipy.stats import poisson

# 定义泊松分布的参数
mu = 3

# 生成泊松分布的概率质量函数
x = np.arange(0, 15)
y = poisson.pmf(x, mu)

# 绘制泊松分布的PMF
plt.bar(x, y)
plt.title('Poisson Distribution PMF')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.show()

1.1.2 概率分布的应用

概率分布在实际问题中有着广泛的应用，例如在金融领域中用于风险评估、在生物学中用于基因表达分析等。通过理解和应用这些概率分布，可以更好地分析和解释数据。

1.2 假设检验

假设检验是统计学中用于判断某个假设是否成立的方法。在SciPy中，scipy.stats模块提供了多种假设检验的函数，包括t检验、卡方检验等。

1.2.1 t检验

t检验是一种用于比较两个样本均值是否相等的假设检验方法。在SciPy中，可以使用ttest_ind函数来进行独立样本t检验。

from scipy.stats import ttest_ind

# 生成两个样本数据
sample1 = np.random.normal(loc=0, scale=1, size=100)
sample2 = np.random.normal(loc=0.5, scale=1, size=100)

# 进行独立样本t检验
t_stat, p_value = ttest_ind(sample1, sample2)

print(f'T-statistic: {t_stat}')
print(f'P-value: {p_value}')

T-statistic: -3.9321361472650316
P-value: 0.00011638454652718614

##### 1.2.2 卡方检验
from scipy.stats import ttest_ind

# 生成两个样本数据
sample1 = np.random.normal(loc=0, scale=1, size=100)
sample2 = np.random.normal(loc=0.5, scale=1, size=100)

# 进行独立样本t检验
t_stat, p_value = ttest_ind(sample1, sample2)

print(f'T-statistic: {t_stat}')
print(f'P-value: {p_value}')

Chi2-statistic: 0.0
P-value: 1.0
Degrees of Freedom: 1
Expected Frequencies: 
[[10. 20.]
 [20. 40.]]

1.3 回归分析

回归分析是一种用于研究变量之间关系的统计方法。在SciPy中，scipy.stats模块提供了线性回归的函数，可以用于拟合线性模型并进行预测。

1.3.1 线性回归

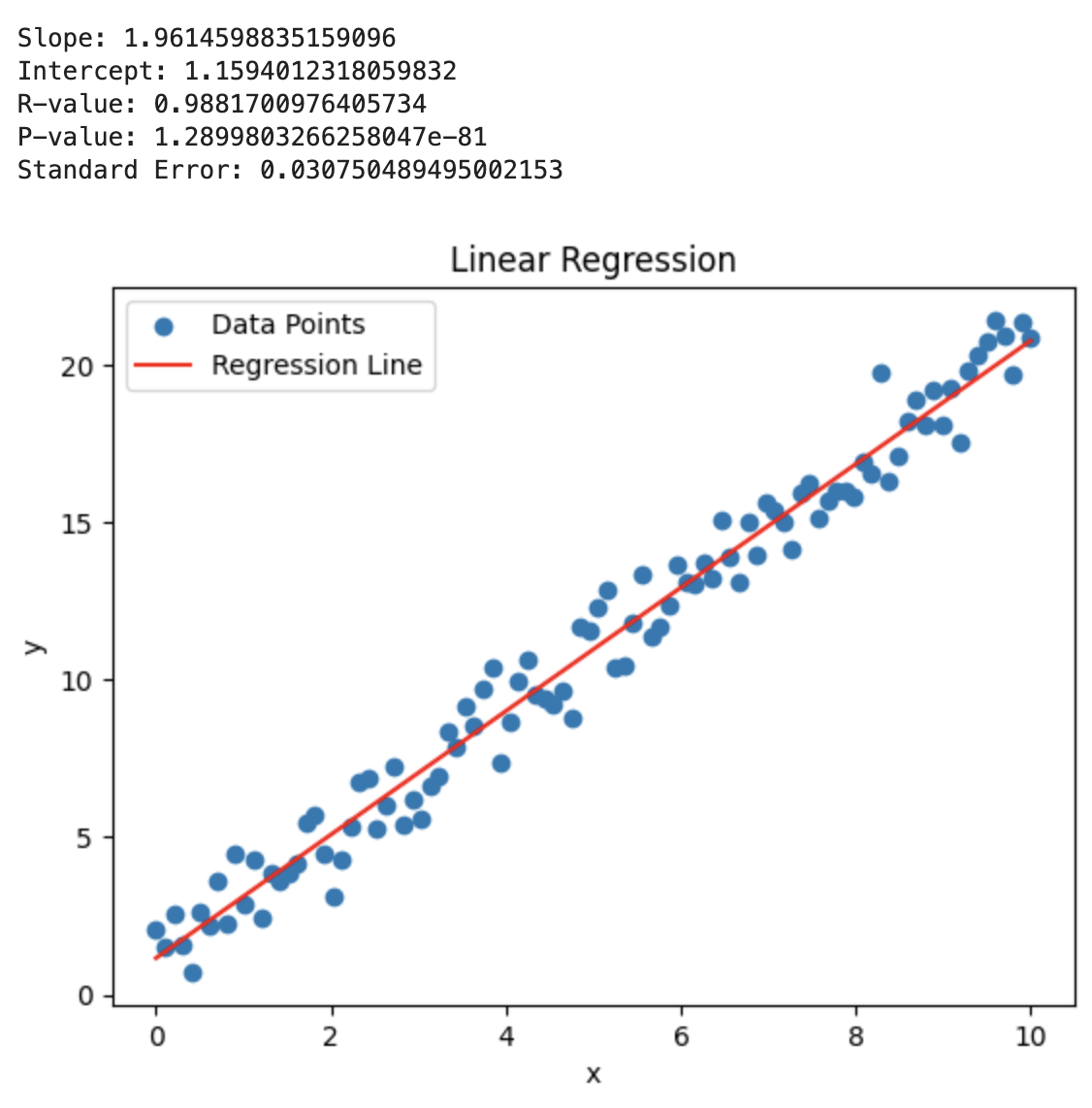
线性回归是一种简单的回归分析方法，用于拟合一个线性模型来描述因变量和自变量之间的关系。在SciPy中，可以使用linregress函数来进行线性回归。
在这里插入图片描述