19杭电多校第七场 1006 Final Exam （田忌赛马）

最新推荐文章于 2022-11-12 22:48:04 发布

原创最新推荐文章于 2022-11-12 22:48:04 发布 · 231 阅读

0 ·

CC 4.0 BY-SA版权

本文探讨了一个考试复习策略问题，采用田忌赛马的思路来解决如何用最少时间复习以确保通过特定数量的题目。文章详细解释了算法思路，并提供了代码实现。

题目链接
http://acm.hdu.edu.cn/showproblem.php?pid=6651

题意

要考试了，一共有n道题目，考试题目的分值是 [0 ~ m]分，但是所有题目的分数之和为 m 。
如果某道题的分值是 x 分，你能够通过这道题的前提是：你对这个题目的知识点复习过x + 1小时。
你要进行复习，以保证你可以考过 k 道题目。

问最少的复习时间。

思路

田忌赛马的思路，尽可能的卡掉复习时间少的题目。

首先，我们进行复习，明天要保证可以通过 k 道题目，也就是说最坏情况下也要能够通过k道题目。

最坏情况是什么？就是m的分配问题，m值被用来分配，使我们能够做出来的题目尽可能少，分配的策略自然是，尽可能分配分值，使得我复习时间最短的那几个题目的复习时间都与它们的分值一样，这样这道题目就刚好做不出来了。

也就是说自己复习时间短的题目刚好被卡掉、不会做了。在被卡掉的题目最多的情况下，还能剩 k 道能做出来的题目。

因此，可以确定的是，最坏情况下，我复习的时间最大的k - 1道题，刚好题目的分值都是0分。

接着，我们要让我们的时间尽可能短，也就是说，要把m的值分配给 n - k + 1道题目，我们做法肯定是平均分配，这里记平均的花费时间为 T。

而m的值在分配时，在卡到 m 的值能够卡到的最后一道题目时，可能刚刚好够把这道题目卡掉，也可能 m 剩余的值不够把这道题目卡掉。

如果这道题目刚好被卡掉，那么后面的k道题目都复习T+1小时。
如果这道题目没有被卡掉，那么后面的k道题目都复习T小时。
这样得到的时间肯定是最短的时间。

这里自己画个图，很好理解得，就这两种情况。黑色的是被卡掉的时间，柱子的高度是每道题目复习的时间。
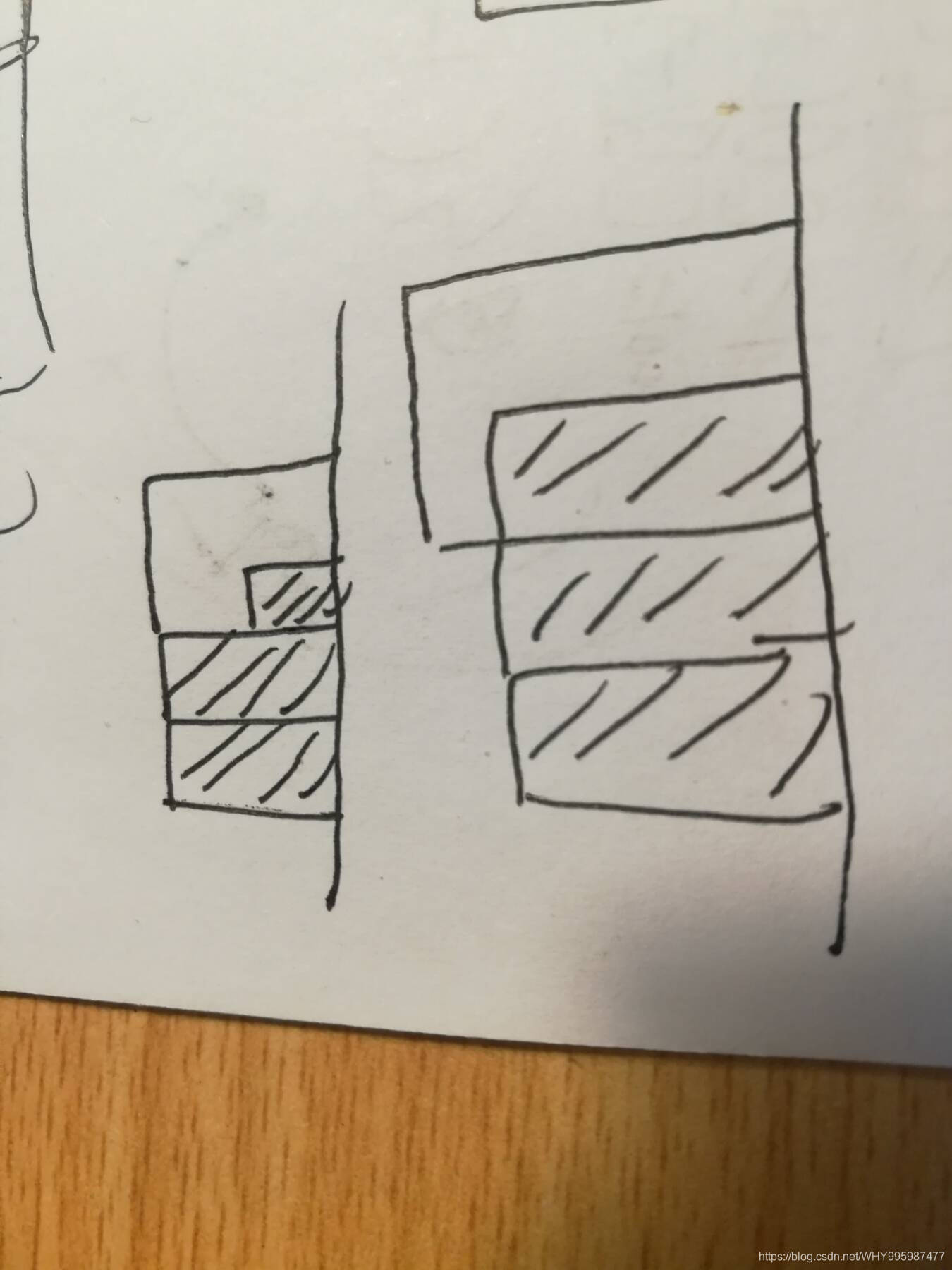
在这里插入图片描述
代码也好理解。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        ll n, m, k;
        cin >> n >> m >> k;
        if(k == n)
        {
            cout << (m + 1) * k << endl;
            continue;
        }
        ll ans = m + 1;
        ll h = m / (n - k + 1) + 1;
        ans += h * (k - 1);
        cout << ans << endl;
    }
    return 0;
}