poj 1681 Painter's Problem（高斯消元）

Painter's Problem

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4224		Accepted: 2043

Description

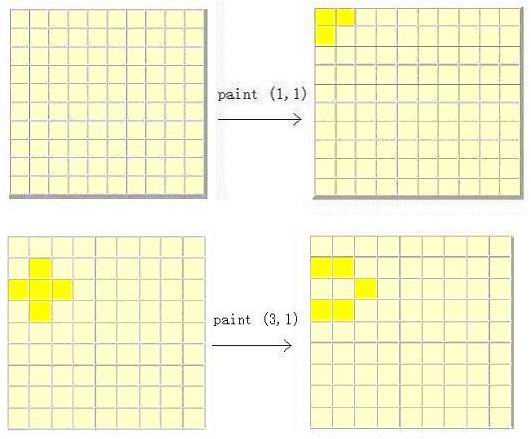
There is a square wall which is made of n*n small square bricks. Some bricks are white while some bricks are yellow. Bob is a painter and he wants to paint all the bricks yellow. But there is something wrong with Bob's brush. Once he uses this brush to paint brick (i, j), the bricks at (i, j), (i-1, j), (i+1, j), (i, j-1) and (i, j+1) all change their color. Your task is to find the minimum number of bricks Bob should paint in order to make all the bricks yellow.

Input

The first line contains a single integer t (1 <= t <= 20) that indicates the number of test cases. Then follow the t cases. Each test case begins with a line contains an integer n (1 <= n <= 15), representing the size of wall. The next n lines represent the original wall. Each line contains n characters. The j-th character of the i-th line figures out the color of brick at position (i, j). We use a 'w' to express a white brick while a 'y' to express a yellow brick.

Output

For each case, output a line contains the minimum number of bricks Bob should paint. If Bob can't paint all the bricks yellow, print 'inf'.

Sample Input

2
3
yyy
yyy
yyy
5
wwwww
wwwww
wwwww
wwwww
wwwww

Sample Output

0
15

题意：和poj1222差不多，这里还要求出是否有解。

思路：把矩阵a变成阶梯矩阵后，若出现矛盾方程（即系数部分全为0，常数不为0），则无解。

AC代码：

#include <iostream>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <queue>
#include <stack>
#include <ctime>
#include <vector>
#include <algorithm>
#define ll __int64
#define L(rt) (rt<<1)
#define R(rt)  (rt<<1|1)

using namespace std;

const int INF = 2000000000;
const int maxn = 250;

int a[maxn][maxn];
int n, m;
int d[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
bool ok(int x, int y){
    if(x >= 0 && x < m && y >= 0 && y < m) return true;
    return false;
}
void gauss(){
    int row = 0, col = 0;
    while(row < n && col < n)
    {
        int id = row;
        for(int i = row + 1; i < n; i++)
        if(abs(a[i][col]) > abs(a[id][col]))
        id = i;
        if(a[id][col])
        {
            for(int i = col; i <= n; i++)
            swap(a[row][i], a[id][i]);
            for(int i = row + 1; i < n; i++)
            if(a[i][col])
            {
                for(int j = col; j <= n; j++)
                a[i][j] ^= a[row][j];
            }
            row++;
        }
        col++;
    }
    for(int i = row; i < n; i++)
    if(a[i][n])
    {
        printf("inf\n");
        return;
    }
    int ans = 0;
    for(int i = row - 1; i >= 0; i--)
    {
        for(int j = i + 1; j < n; j++)
        a[i][n] ^= (a[j][n] && a[i][j]);
        if(a[i][n]) ans++;
    }
    printf("%d\n", ans);
}
int main()
{
    int t;
    char s[maxn];
    scanf("%d", &t);
    while(t--)
    {
        memset(a, 0, sizeof(a));
        scanf("%d", &m);
        n = m * m;
        for(int i = 0; i < m; i++)
        {
            scanf("%s", s);
            for(int j = 0; j < m; j++)
            {
                if(s[j] == 'y') a[i * m + j][n] = 0;
                else a[i * m + j][n] = 1;
            }
        }
        for(int i = 0; i < m; i++)
        for(int j = 0; j < m; j++)
        {
            int row = i * m + j;
            a[row][row] = 1;
            for(int k = 0; k < 4; k++)
            {
                int nx = i + d[k][0], ny = j + d[k][1];
                if(ok(nx, ny)) a[row][nx * m + ny] = 1;
            }
        }
        gauss();
    }
    return 0;
}