自然语言处理总复习（三）—— Markov模型

一、HMM（隐马尔科夫模型）的形式化定义

二、隐马尔可夫模型的三个基本问题及其算法

（一）评估问题

1. 问题描述

给定一个观察序列 $O=O_1{O}_2...O_T$和模型$\lambda$，如何计算给定模型$\lambda$下观察序列$O$的概率$P(O|\lambda )$.

2. 解决方法

(1) 前向算法

(2) 后向算法

（二）解码问题

1. 问题描述

给定一个观察序列$O=O_1{O}_2\dots O_T$和模型$\lambda$，如何计算状态序列$Q=q_1{q}_2\dots q_T$, 使得该状态序列能“最好地解释”观察序列。

所求的$Q$应当时在某个准则下时“最优”的，因此也成$Q$为最优路径，解码问题即是确定最优路径的问题。

该问题可以形式化为：
$$Q^{\ast }=\underset{Q}{\mathrm{argmax}}P(Q|O,\lambda )$$

2. 解决方法 —— Viterbi算法（基于Viterbi变量的动态规划算法）

Viterbi变量 在时间 t 沿状态序列 $q_1{q}_2\dots q_t$且$q_t=S_i$而产生出$O_1{O}_2\dots O_t$的最大概率，即：
$${\delta }_t(i)=\underset{q_1,q_2,\dots ,q_{t-1}}{\max }P(q_1,q_2,\dots ,q_t=S_i,O_1,O_2,\dots ,O_t|\lambda )$$

Viterbi变量说明的是：从初始状态到 t 时刻的状态$S_i$的所有路径中的最佳转移路径
（判断最佳的条件：这条路径代表的状态能够产生相应的观测序列的概率最大）

（三）学习问题

1. 问题描述

2. 解决方法

三、隐马尔科夫模型的应用

（一）词性标注

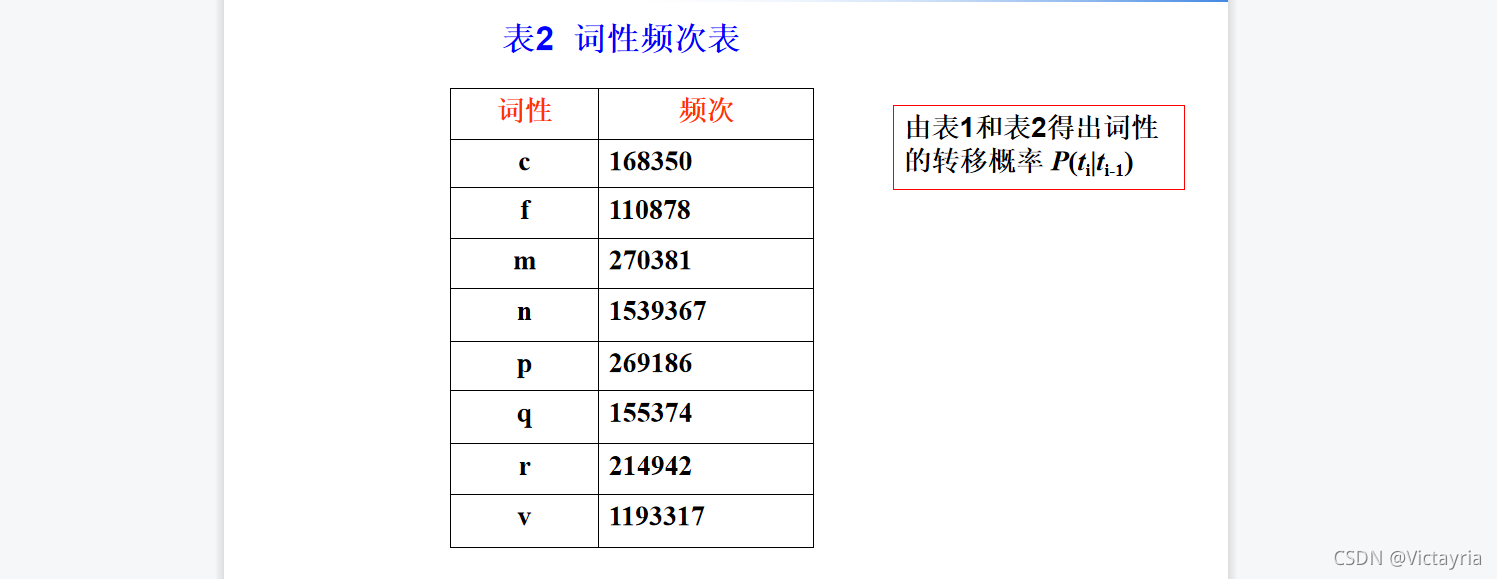
四、隐马尔可夫模型总结