接收通道处理一文读懂雷达信号采样基础

原创于 2025-12-11 18:21:33 发布 · 633 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#雷达技术

国防科技类专栏收录该内容

9 篇文章

订阅专栏

信号采样基础：从零开始的清晰解释

大家好！今天我要和大家聊聊信号采样这个在数字信号处理中非常重要的基础概念。我将从最基础的原理开始，用简单易懂的语言和必要的数学推导，帮助大家真正理解这个看似复杂的概念。

1. 什么是信号采样？

想象一下，你正在听一首美妙的音乐。音乐是一种连续时间信号——它在时间上是连续的，每个时刻都有声音。但是，我们的电脑和手机只能处理数字信号，也就是在特定时刻的离散值。

采样就是将连续时间信号转换为离散时间信号的过程。就像把连续的音乐"截取"成一个个小片段，每个片段记录一个时刻的声音大小。

2. 为什么需要采样？

在数字世界中，我们只能处理离散的数据。为了让计算机能够处理模拟信号（如声音、雷达回波、图像等），我们必须将它们转换成数字形式。

3. 采样的数学模型

3.1 采样过程的直观理解

想象一个连续时间信号 $x(t)$ ，如图所示：

1x(t)
2^
3|    .     .
4|   . .   . .
5|  .   . .   .
6| .     .     .
7+-----------------> t

现在，我们以固定的时间间隔 $T$ （采样周期）来"截取"这个信号：

1x(t)
2^
3|    .     .     .
4|   . .   . .   . .
5|  .   . .   .   .
6| .     .     .     .
7+-----------------> t
8  T   2T   3T   4T

在每个时间点 $t=nT$ n 为整数，我们记录信号的值。

3.2 理想采样的数学表示

理想采样可以表示为连续信号与一个单位冲激脉冲序列的乘积：

这个公式表示：采样后的信号是由一系列冲激组成，每个冲激的强度等于原信号在该时刻的值。

3.3 采样频率与角频率

4. 采样定理（奈奎斯特采样定理）

4.1 采样定理的直观理解

想象一个正弦波，它的频率越高，波形变化越快。如果采样太慢，我们可能会"错过"波峰和波谷，导致采样后的信号看起来像是一个频率更低的正弦波。

例如，一个频率为 100 Hz 的正弦波，如果用 150 Hz 的采样率采样，采样后的波形可能看起来像 50 Hz 的正弦波（150 - 100 = 50）。

4.2 采样定理的数学推导

4.2.1 信号的频谱表示

4.2.2 采样后的频谱

4.2.3 频谱混叠

4.2.4 奈奎斯特采样定理

为了确保采样后的信号能够无失真地恢复原信号，必须满足：

这就是著名的奈奎斯特采样定理。

推导过程：

4.2.5 为什么是 2 倍？

为了确保频谱不重叠，我们需要保证每个周期频谱之间有足够的间隔。这个间隔至少要等于原信号最高频率，所以采样频率至少要是最高频率的 2 倍。

5. 实际应用中的采样

5.1 为什么工程中通常用 2.56~4 倍的采样率？

5.2 采样过程中的实际考虑

6. 一个简单的例子

7. 总结

8. 为什么理解采样定理很重要？

理解采样定理对以下领域至关重要：

雷达系统：雷达回波需要被采样以进行数字处理
音频处理：CD 音质使用 44.1 kHz 采样率（满足 2 × 22.05 kHz 的人耳听觉范围）
图像处理：数字相机和视频需要采样和量化
通信系统：现代通信依赖于采样和数字信号处理

9. 一个实用的建议

当你设计一个采样系统时，请记住：

复数信号及其频谱分析

引言

在信号处理和通信领域，复数信号是描述连续时间信号的重要工具。复数信号不仅包含幅度信息，还包含了相位和频率信息。通过频谱分析，可以了解信号在频域上的特性，这对于信号的采样、传输以及处理至关重要。本文将详细探讨复数信号的频谱表示、带宽特性以及相关的数学工具。

复数信号与其频谱

复数信号通常以复指数的形式表示，例如：

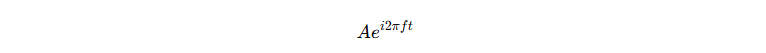
复数信号的频谱表示

复数信号的频谱分布通常表现为多个正负频率成分。在分析时，常用的数学工具就是复指数。对于一个周期性的信号，如果它包含多个频率分量，通常可以通过傅里叶变换来将其分解为多个不同频率的正弦和余弦成分。

复数信号的频谱分析在很多应用中都有重要意义。例如，在通信系统中，信号的频率分布直接影响信号的带宽和传输效率。通过对信号进行傅里叶变换，我们可以得到信号在频域上的具体表现形式。文中提到，对于复数信号来说，频谱不仅仅是简单的正频率和负频率分量，它们的相对幅度和相位在信号的传输过程中会发生变化。

采样与带宽

信号的采样频率是频谱分析中的一个关键问题。如果信号的频率分布超过了采样频率的一半，则会出现混叠现象，从而导致信号无法准确重建。这也是为什么在信号采样时需要遵循奈奎斯特采样定理，即采样频率必须至少为信号带宽的两倍。

对于复数信号来说，采样时的带宽问题尤为重要。如果信号的频率分布在采样频率范围内，那么我们可以通过适当的采样间隔来准确重建信号。然而，若频率分布超过了采样频率的一半，那么采样后的信号会丧失一些频率成分，导致信息丢失。

复频谱的对称性

复数信号的频谱有一个显著的特点——其正负频率部分是对称的。这种对称性对于理解信号的能量分布非常重要。在一些情况下，信号的频谱会具有某种特殊的对称性，例如，如果信号的频率分布是对称的，那么它的复频谱也会呈现对称结构。

这种对称性不仅在数学上有着简洁的表示，而且在实际信号处理中也具有重要的应用。例如，在一些通信系统中，信号的复频谱对称性可以帮助我们优化系统的带宽利用率，并减少信号的失真。

频谱的复指数表示

在频谱分析中，我们常使用复指数形式来表示信号的频率分量。文中提到的一个重要公式是：

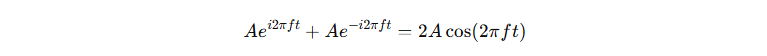
这个公式表明，正负频率的复数信号相加后，得到的是一个实数信号（由余弦函数表示）。这在信号处理中非常有用，因为许多实际信号都可以表示为正负频率分量的组合。

带宽与频率分布

复数信号的带宽是指信号在频域中所占据的频率范围。信号的频谱分布直接影响其带宽，带宽的大小决定了信号可以传输的信息量。在实际应用中，带宽限制对于信号的设计和传输效率至关重要。复数信号的频率分布如果过于宽广，可能会超出通信系统的带宽限制，从而导致信号失真或误码率增加。

通过适当的频谱分析，我们可以判断一个复数信号的带宽是否符合传输要求。在很多通信系统中，信号的带宽和信道的频率资源之间需要进行优化匹配。

结论

复数信号的频谱分析为我们提供了理解信号在频域上的特性的重要工具。通过复指数的表示方法，我们可以清晰地看到信号的正负频率分量，并利用这些分量进行信号重建和优化设计。在实际应用中，采样定理、带宽限制和频谱对称性是设计高效通信系统的核心问题。因此，深入理解复数信号的频谱特性对信号处理、通信系统的优化以及其他相关领域都有着重要的意义。

复数信号频谱分析代码

import numpy as np
import matplotlib.pyplot as plt

# ---------------------------
# 1. 参数配置
# ---------------------------
Fs = 1000        # 采样频率 (Hz)
T  = 1           # 信号时长 (秒)
t  = np.linspace(0, T, int(Fs * T), endpoint=False)   # 时间轴

# 复数信号的频率和振幅
f0 = 50           # 频率 (Hz)
A  = 1.5          # 幅度
phi = np.pi/3     # 初相位

# ---------------------------
# 2. 复数信号生成
# ---------------------------
# 复指数形式
x_complex = A * np.exp(1j * (2 * np.pi * f0 * t + phi))

# 信号的实部和虚部
x_real = np.real(x_complex)
x_imag = np.imag(x_complex)
x_mag  = np.abs(x_complex)
x_phase = np.angle(x_complex)

# ---------------------------
# 3. 傅里叶变换
# ---------------------------
X = np.fft.fft(x_complex)
freqs = np.fft.fftfreq(len(t), 1/Fs)

# 按频率排序 (低->高)
idx = np.argsort(freqs)
freqs_sorted = freqs[idx]
X_sorted     = X[idx]

# ---------------------------
# 4. 可视化
# ---------------------------
plt.figure(figsize=(14, 12))

# 时域信号
plt.subplot(4,1,1)
plt.plot(t, x_real, label="Real Part")
plt.plot(t, x_imag, label="Imag Part", linestyle='--')
plt.title("Complex Signal in Time Domain")
plt.xlabel("Time (s)")
plt.ylabel("Amplitude")
plt.legend()

# 幅度与相位
plt.subplot(4,1,2)
plt.plot(t, x_mag, label="Magnitude")
plt.plot(t, x_phase, label="Phase")
plt.title("Signal Magnitude & Phase")
plt.xlabel("Time (s)")
plt.ylabel("Value")
plt.legend()

# 频域幅度谱 (线性)
plt.subplot(4,1,3)
plt.stem(freqs_sorted, np.abs(X_sorted), 'b', markerfmt=" ", basefmt="-b")
plt.title("Spectrum |X(f)|")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Magnitude")
plt.xlim(-200, 200)

# 频域实部/虚部
plt.subplot(4,1,4)
plt.plot(freqs_sorted, np.real(X_sorted), label="Real")
plt.plot(freqs_sorted, np.imag(X_sorted), label="Imag")
plt.title("Spectrum Components (Real/Imag)")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Value")
plt.legend()
plt.xlim(-200, 200)

plt.tight_layout()
plt.show()

运行结果

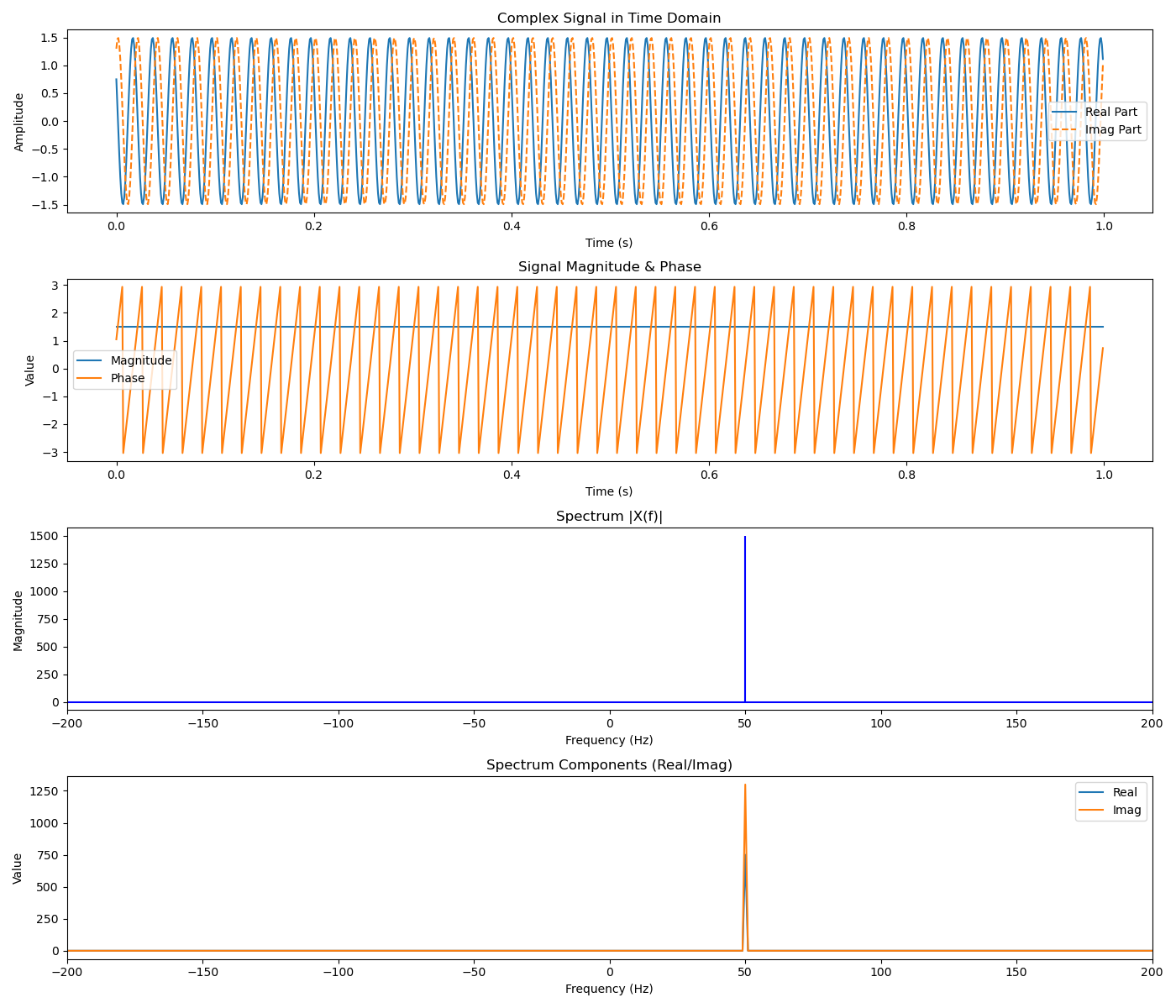
雷达系统中采样率选择的理论与实践

1. 理论基础：为何“带宽”是核心？

1.1 采样定理在雷达中的修正

1.2 带宽与性能的关联

2. 不同雷达体制的采样率选择策略

根据雷达类型和信号处理需求的不同，工程上对采样率有分级要求。

2.1 一般脉冲雷达（Standard Pulse Radar）

2.2 脉冲压缩雷达（Pulse Compression Radar）

适用场景：需要高距离分辨率、高信噪比的精密雷达（如火控、成像）。

2.3 FMCW 雷达（调频连续波）

适用场景：车载毫米波雷达、高度计。
特殊机制：FMCW 雷达通过混频将高频信号转化为低频的拍频信号 (Beat Frequency)。采样对象是拍频，而非发射信号。

3. 进阶技术：带通采样 (Bandpass Sampling)

4. 工程决策流程与速查表

4.1 采样率设计四步法

4.2 常见雷达系统采样率速查表

雷达类型	信号带宽 (B)	推荐采样倍数	典型采样率 (fs)	核心考量依据
S波段脉冲雷达	500 MHz	2.5B ~ 3B	1.25 ~ 1.5 GHz	平衡滤波器设计难度与成本
X波段脉冲压缩	1 GHz	3B ~ 5B	3 ~ 5 GHz	确保脉冲压缩后的旁瓣抑制性能
毫米波 FMCW	150 MHz	N/A (基于拍频)	~ 1 MHz	采样对象为拍频，极大降低数据量
低频雷达 (HF/VHF)	10 MHz	2.5B	25 ~ 50 MHz	带宽较窄，处理相对容易