文章目录
1.1. int类型变量的声明、定义、赋值
在C/C++语言中,有很多种类型,而整型是用的最多的
声明一个变量:
int num; // 声明一个整型变量
声明并初始化一个变量:
int cnt = 0; // 声明并初始化一个变量
先声明一个变量,再赋值:
// 先声明一个变量 再赋值
int exm; // 声明一个变量,它的值是随机的
exm = 10;// 给这个变量赋值
上面这两行代码和int exm = 10;的作用是一样的,但是赋值和初始化是两个不同的操作,
赋值是给已经存在的变量进行操作,初始化是在变量定义时进行操作
1.2. 未初始化的变量
必须强调这里未初始化的危险。如果一个变量没有初始化,C/C++ 编译器不会报告错误,甚至不会发出警告。C/C++标准中未初始化变量的值也没有明确定义。你可能会从一个未初始化的变量中得到一个随机值。为了程序的健壮性,强烈建议初始化变量,哪怕不知道这个变量到底值为多少,初始化成0也是很好的
int main() {
int num1;
int num2 = 10;
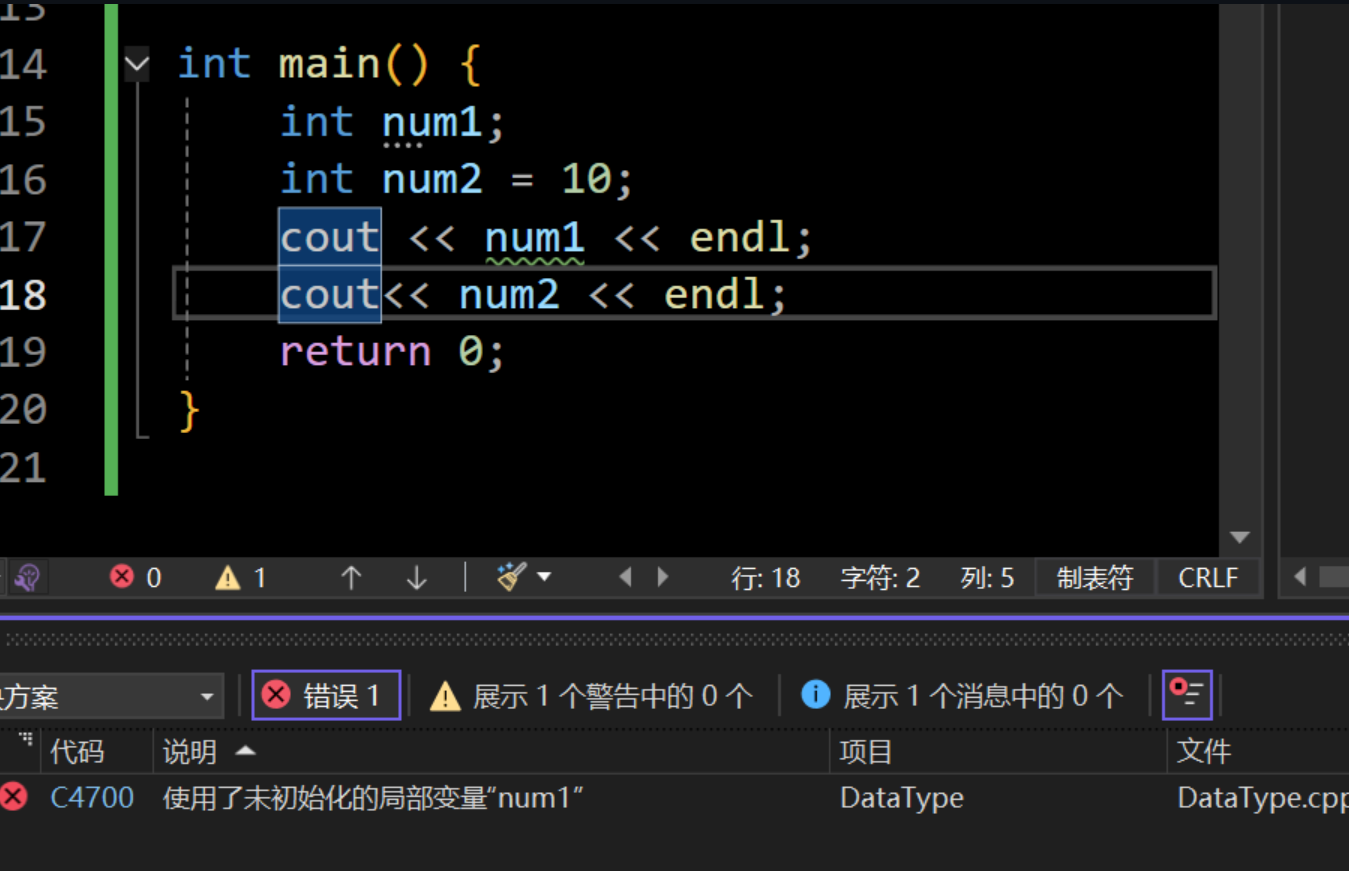
cout << num1 << endl << num2 << endl;
}
VS2022强制检查,报错了
使用C语法也一样报错
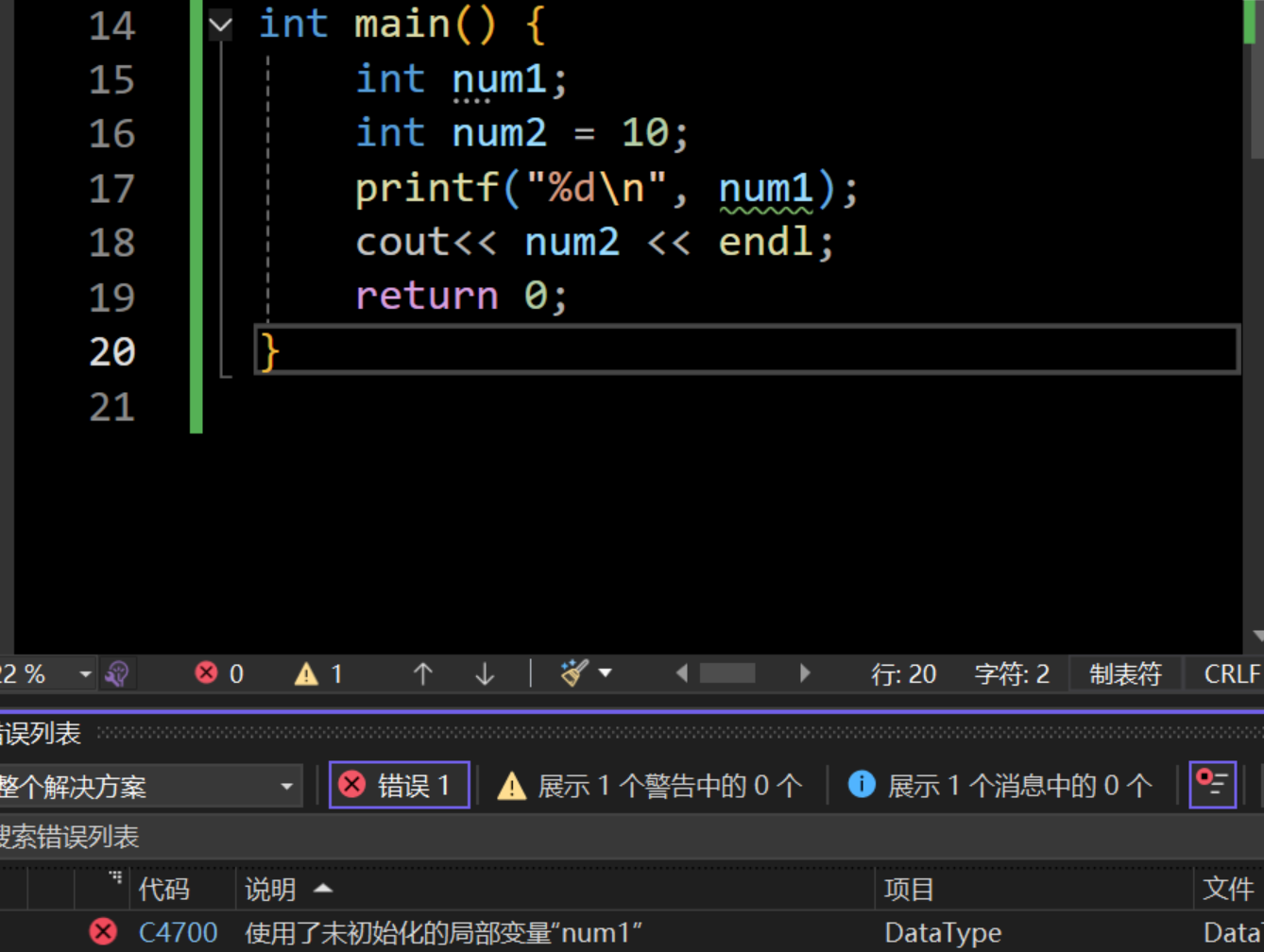
2. 其他的整型
int 的宽度(以位为单位)在 C 和 C++ 标准中并不是固定的。标准 int 应具有 32 位。除了 int,还有 short int、long int 和 long long int``short int 是 16 位。int 是 16 位或 32 位。long int 是 32 位或 64 位(取决于编译器)。long long int 是 64 位。char 也是一种常用的整数类型。有人可能会感到困惑,认为 char 仅用于字符。由于字符被编码为整数值,char 确实是一种整数类型,并且具有 8 位。char 对英语字符来说足够宽,但对中文和其他一些字符则不够。char16_t 和 char32_t 已在 C++11 中引入,表示 16 位和 32 位的范围。
char c = 'C'; // ASCII码为80
char c = 80;// 十进制80
char c = 0x50;// 十六进制50 转为十进制80
上面这三行代码是等效的,在我们编码时,看着每个变量的类型不同,其实到计算机底层,所有数据都被表示成01串了,机器只能识别01两个指令
以下是各个整型类型所占空间大小
| 类型 | 所占字节大小 |
|---|---|
char | 8 |
short (short int) | 16 |
int | 16 or 32 |
long (long int) | 32 or 64 |
long long (long long int) | 64 |
我们可以用sizeof操作符来获取类型大小
int main() {
cout << sizeof(char) << endl;
cout << sizeof(short) << endl;
cout << sizeof(int) << endl;
cout << sizeof(long) << endl;
cout << sizeof(long long) << endl;
return 0;
}
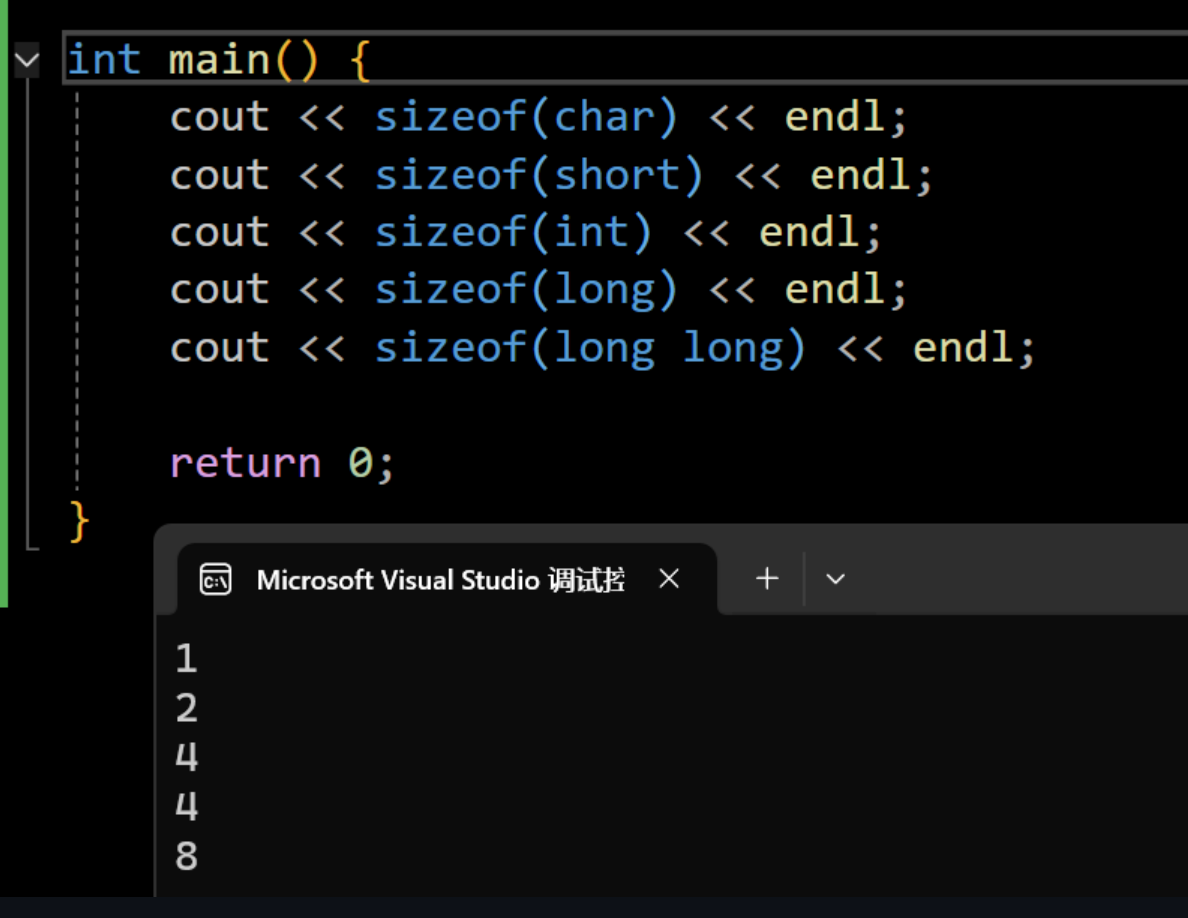
在我的机器上long是四字节
有符号和无符号数
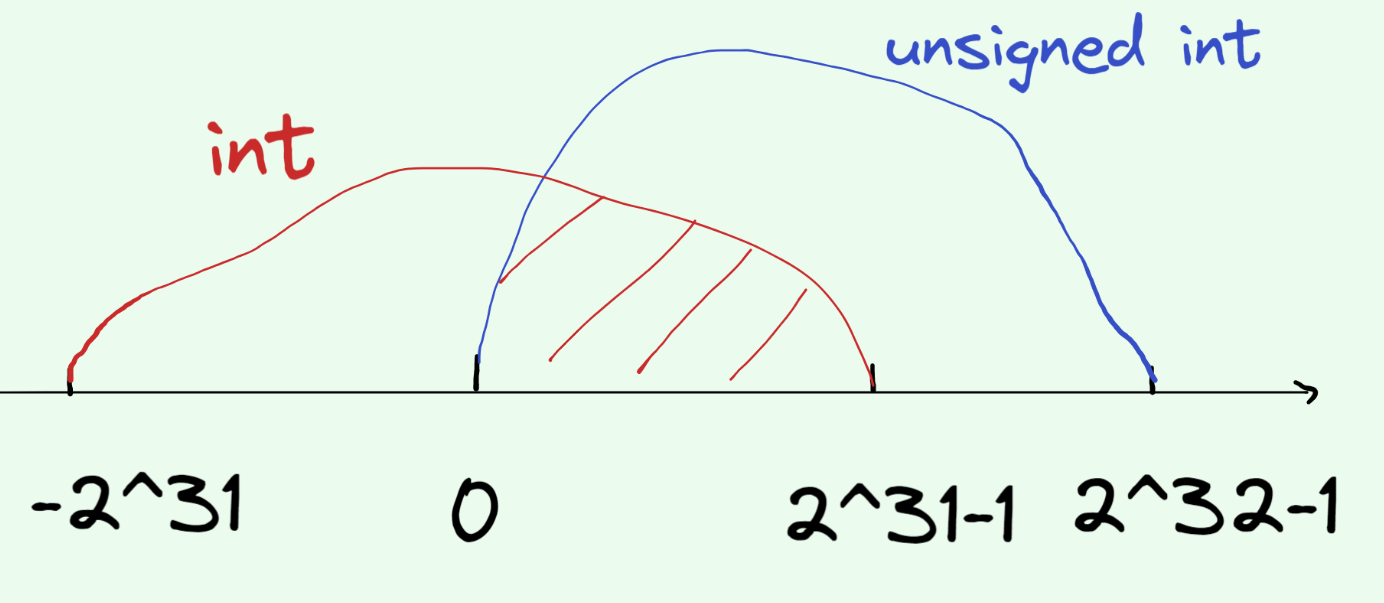
signed 或 unsigned 可以在整数类型名称之前使用,以指示整数是有符号的还是无符号的。当整数是有符号时,关键字 signed 可以省略。这意味着 int 是用于 signed int,而 short 是用于 signed short。如果整数是有符号的,最高位(int 的第 32 位)将是其符号位。如果符号位为 1,则为负数;如果为 0,则为正数。
有符号整数和无符号整数如下面的图所示:
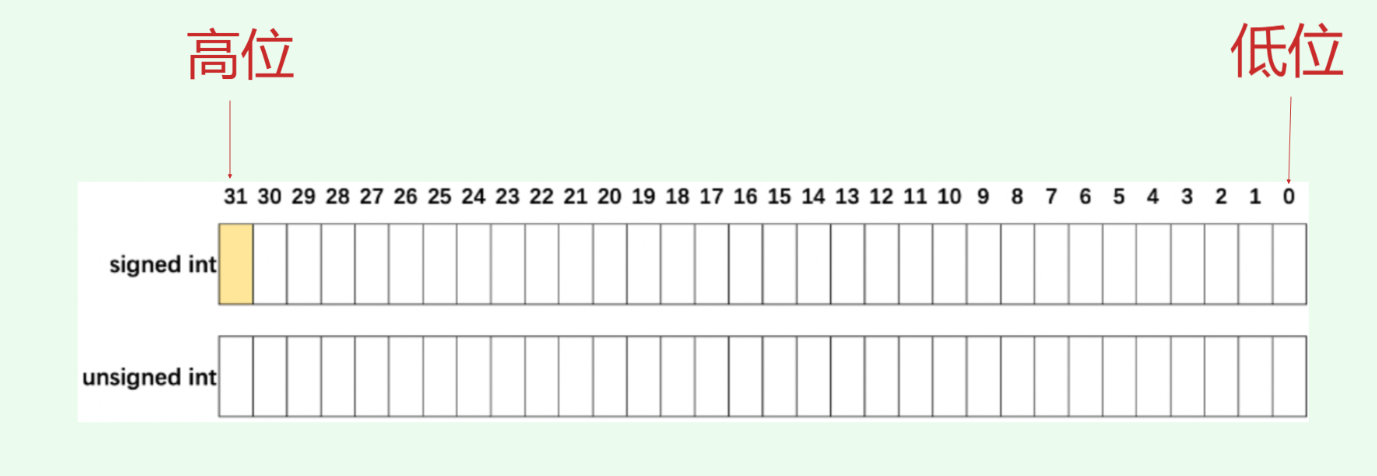
3. 整型数据的存储
3.1. 原码表示法
数据在底层用0和1这两个数存储,一个字节(8bit)可以表达多少个数?————>每个位置两种选择,共八个位置: 2 8 2^8 28个
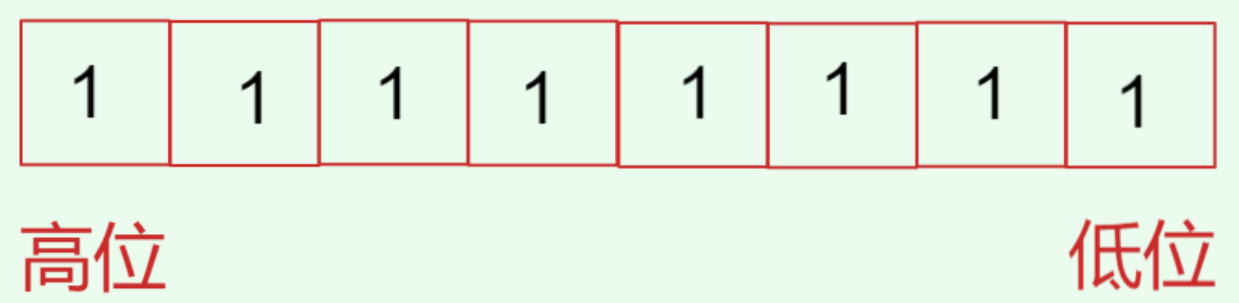
对于无符号数来说,最大的数就是 ( 2 8 − 1 ) (2^8 - 1) (28−1)
那怎么表示负数呢?牺牲最高位作为符号位,符号位为 1,则为负数;如果为 0,则为正数。,这便是原码
这样就能得到以下分类:
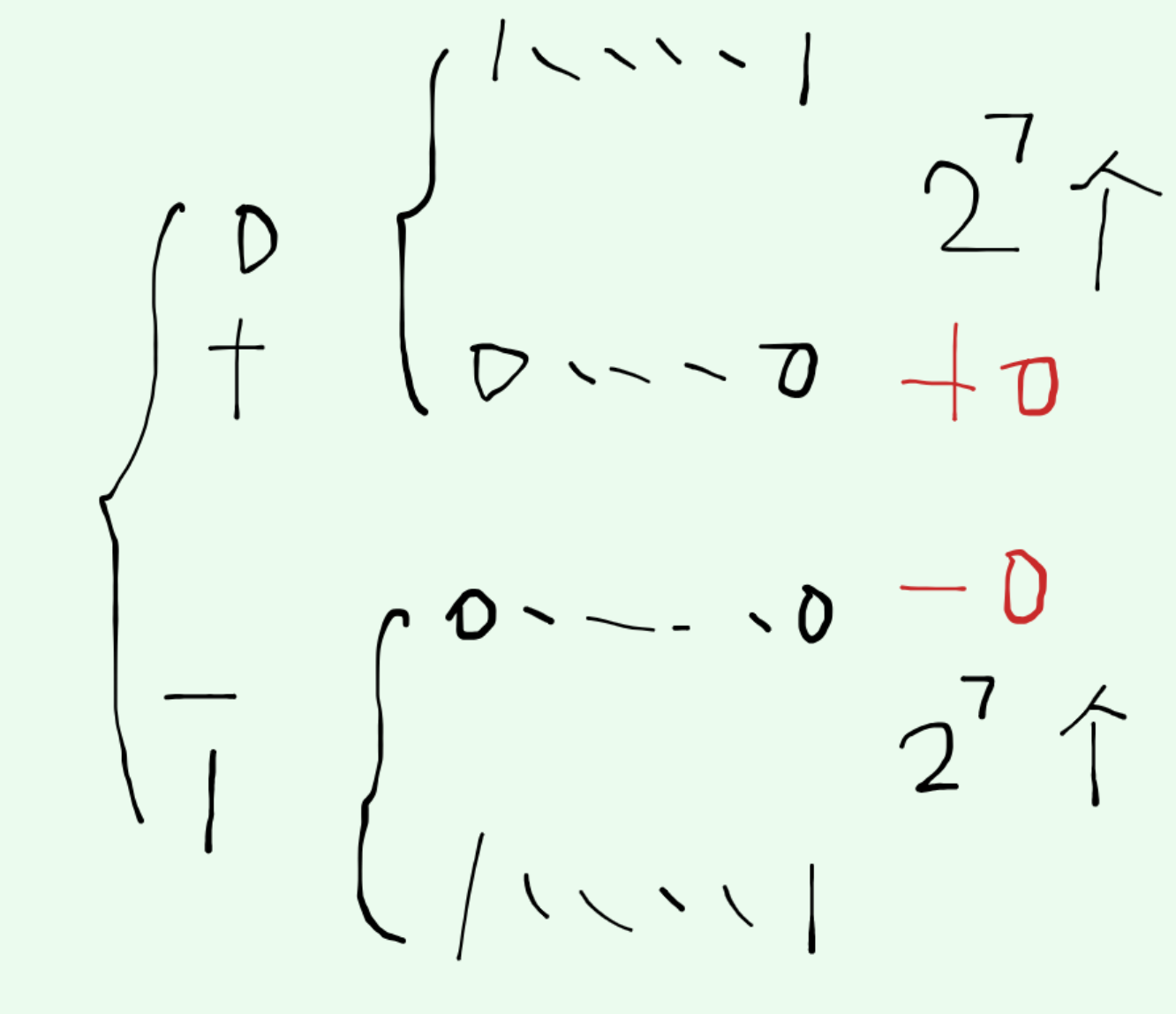
符号位后两个极端,全0或者全1,正数可以表达 2 7 2^7 27个,负数也可以表达 2 7 2^7 27个,但是出现一个问题:0被重复表达了两次!+0和-0,所以,原码表示法出现了缺陷:
- 0的表示并不唯一,计算机是机器,不是人,无法理解多义的表达
- 加法、减法的运算方式并不统一,减法需要借位,逻辑复杂
所以,引入补码
3.2. 补码表示法
3.2.1 模运算的引入
对于一个钟表,假定指针指向了10点的位置,我现在要将其拨到6点位置,有两种方式:
- 倒拨四格: 10 − 4 = 6 10 - 4 = 6 10−4=6
- 顺拨八格: 10 + 8 ——— > 6 10 + 8 ———>6 10+8———>6,转完了一圈,18 % 12 = 6

钟表是一个模十二的系统:那么就可以理解为 10 − 4 = 10 + 8 = 10 + ( 12 − 4 ) 10-4 = 10+8 = 10+(12-4) 10−4=10+8=10+(12−4)
这里的-4和8是相等的关系,那么就可以说8的补码是-4,同样的,9的补码是-3
在模十二的系统中,都遵循着一个原则:互为补码的两个数,不管符号,相加和为12,8+4,9+3,10+2的结果都是12
那么,在一个模 x x x的运算系统中,有两个数 1 1 1 和 − n -n −n,一定满足 1 + n = x 1+n=x 1+n=x
那么就引出了补码的运算:加法和减法的运算逻辑相同
如果做减法,我们只需要加上这个数的补码即可,将减法转换成了加法,这样加减法共用一套逻辑
3.2. 补码表示法
**”8位2进制数“模运算系统(mod 2 8 2^8 28)**中,有两个数 1 1 1 和 − n -n −n,一定满足 1 + n = 2 8 1+n=2^8 1+n=28
现在用 2 8 2^8 28减去一个1,即是
1 0000 0000 - 0000 0001————> 得到1111 1111,这个数,是-1的表达,所以-1的表达,就是 2 8 2^8 28减去1,相当于把原来的0000 0001各位取反再加1————>1111 1111,现在使得1111 1111 + 0000 0001————>1 0000 0000即是 2 8 2^8 28,这便是负数的补码
正数的补码是正数本身,负数的补码是符号位不变,其他位取反,末位加一
例如:-1:原码1000 0001 补码:1111 1111
现在回到之前的分类:

这样原来的-0:1000 0000就可以表示一个更小的数了
我们再将1000 0000转换成原码检查一下:
除了符号位全部取反->1111 1111,末尾+1->1 0000 0000,
八位存不下,最高位截断:0000 0000 ->0 0 + 2 8 = 2 8 0 + 2^8 = 2^8 0+28=28,满足“8位2进制数“模运算系统(mod 2 8 2^8 28)的规则
以下是常见整型的取值范围:
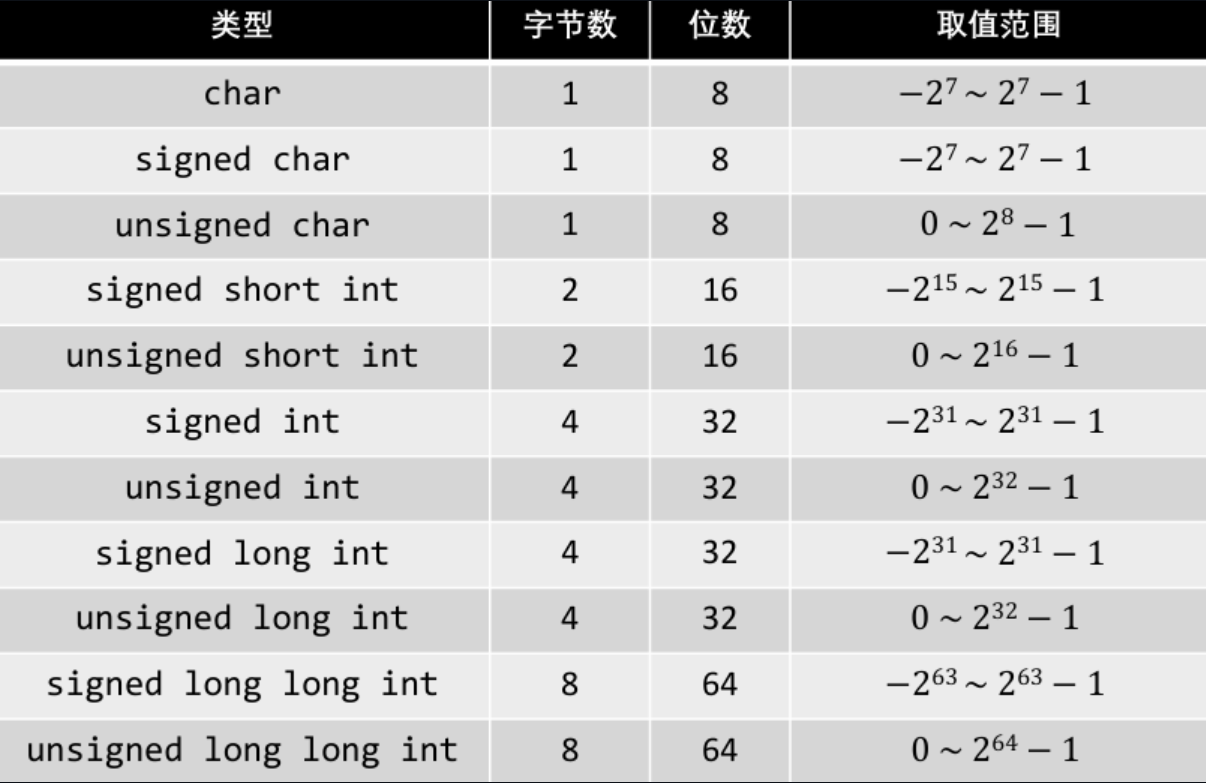
我们可以继续用一个圆来理解:
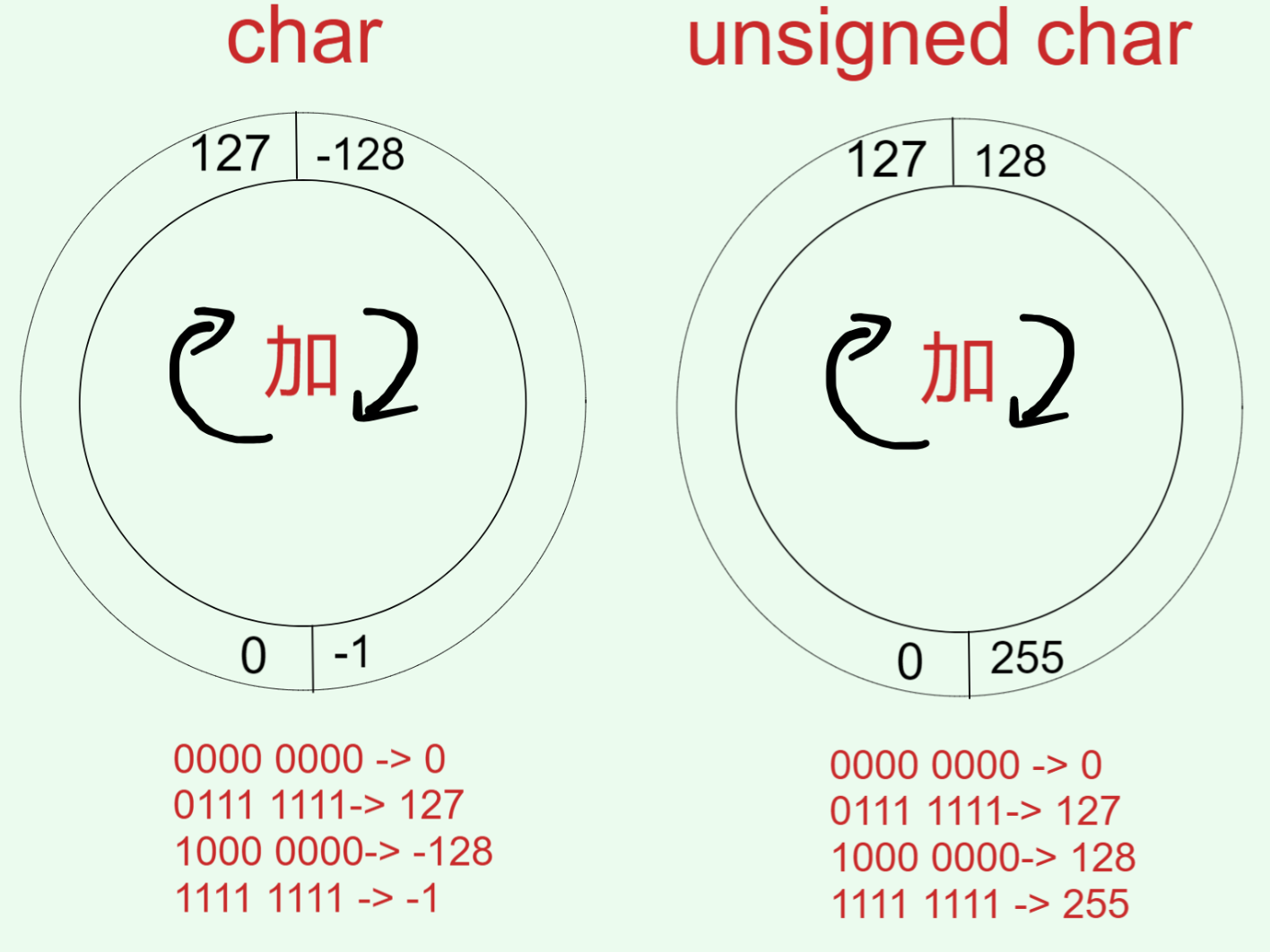
short int等其他类型同理
4. 小案例
4.1. 规定:若运算中同时有无符号和带符号整数,则按无符号整数运算
| 关系运算符 | 类型 | 结果 | 说明 |
|---|---|---|---|
| 0 == 0U | 无符号 | 1 | 同为零 |
| -1 < 0 | 有符号 | 1 | 有符号类型-1<0 |
| -1 < 0U | 无符号 | 0 | 11…11( 2 32 − 1 2^{32}-1 232−1) > 0 |
| 2147483647 > -2147483647 -1 | 有符号 | 1 | 正数 >负数 |
| 2147483647U > -2147483647 - 1 | 无符号 | 0 | 01…1( 2 31 − 1 2^{31}-1 231−1)<10…0( 2 31 2^{31} 231) |
| 2147483647 >(int)2147483647U | 有符号 | 1 | 01…1( 2 31 − 1 2^{31}-1 231−1)>10…0( − 2 31 -2^{31} −231) |
| -1 >-2 | 有符号 | 1 | 有符号类型-1>-2 |
| (unsigned)-1 > -2 | 无符号 | 1 | 11…11( 2 32 − 1 2^{32}-1 232−1) > 11…10( 2 32 − 2 2^{32}-2 232−2) |
对于int和unsigned int:
2
31
−
1
>
−
2
31
2^{31}-1 > -2^{31}
231−1>−231
4.2. 计算机的世界只有0和1,具体怎么解读靠人的定义
int main() {
int x = -1;
unsigned u = 2147483648;
printf("x = %u = %d\n", x, x);
printf("u = %u = %d\n", u, u);
return 0;
}
- 对于变量
x = -1:- 在内存中,
-1作为 32 位有符号整数(补码)存储为全 1:11111111 11111111 11111111 11111111 - 当用
%u(无符号整数格式)输出时,这个二进制被解读为无符号数,值为4294967295(2³²-1) - 当用
%d(有符号整数格式)输出时,正确解读为-1
- 在内存中,
- 对于变量
u = 2147483648:- 作为无符号整数,它的二进制是
10000000 00000000 00000000 00000000 - 当用
%u输出时,正确显示为2147483648 - 当用
%d输出时,这个二进制被解读为有符号整数(补码),由于最高位是 1(符号位),表示这是一个负数。在 32 位有符号整数中,这个值恰好是最小的负数-2147483648
- 作为无符号整数,它的二进制是
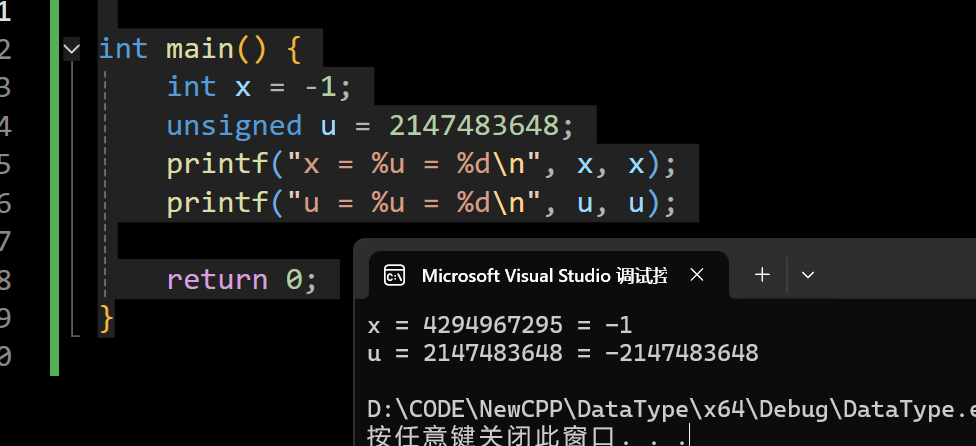
这个例子展示了C/C++整数的二进制存储本质:相同的二进制序列,根据解释方式(有符号 / 无符号)的不同,会呈现出完全不同的数值。格式化字符 %d 和 %u 决定了如何解读内存中的二进制数据,而不是改变数据本身。
int main() {
int b = -1;
char c = -1;
printf("%u,%u\n",b, c);
return 0;
}
- 变量存储分析:
int b = -1:作为 32 位有符号整数,-1的补码表示为全 1(11111111 11111111 11111111 11111111)char c = -1:在大多数系统中char是 8 位,-1的补码表示为11111111
printf输出规则:- 当使用
%u(无符号整数格式)输出时,所有整数类型都会被提升为unsigned int b作为 int 直接转换为 unsigned int,全 1 的 32 位二进制对应4294967295c作为 char 首先进行符号扩展(因为是有符号 char),8 位的11111111扩展为 32 位的11111111 11111111 11111111 11111111,再转换为 unsigned int 也得到4294967295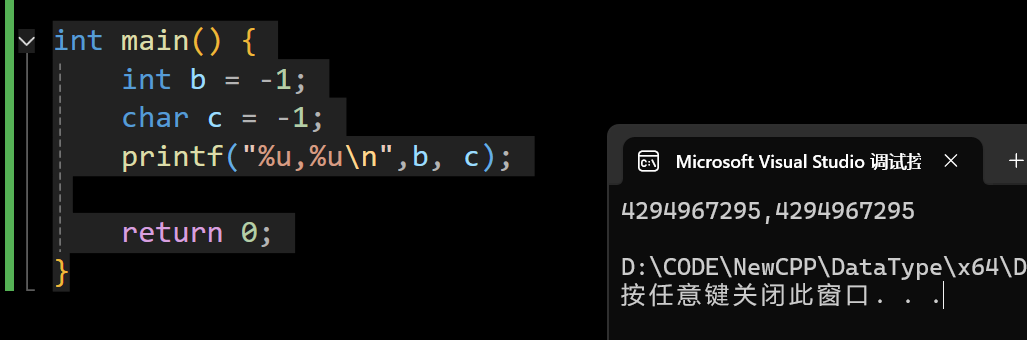
- 当使用
这个例子展示了C/C++整数提升和符号扩展的规则:当小整数类型参与表达式运算或格式化输出时,会先提升为 int (有符号扩展),再根据格式控制符进行相应转换。






















 2772
2772










