二叉树理论基础及遍历方式

二叉树的种类：

二叉树由两种主要形式：满二叉树。完全二叉树

满二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

如图所示：

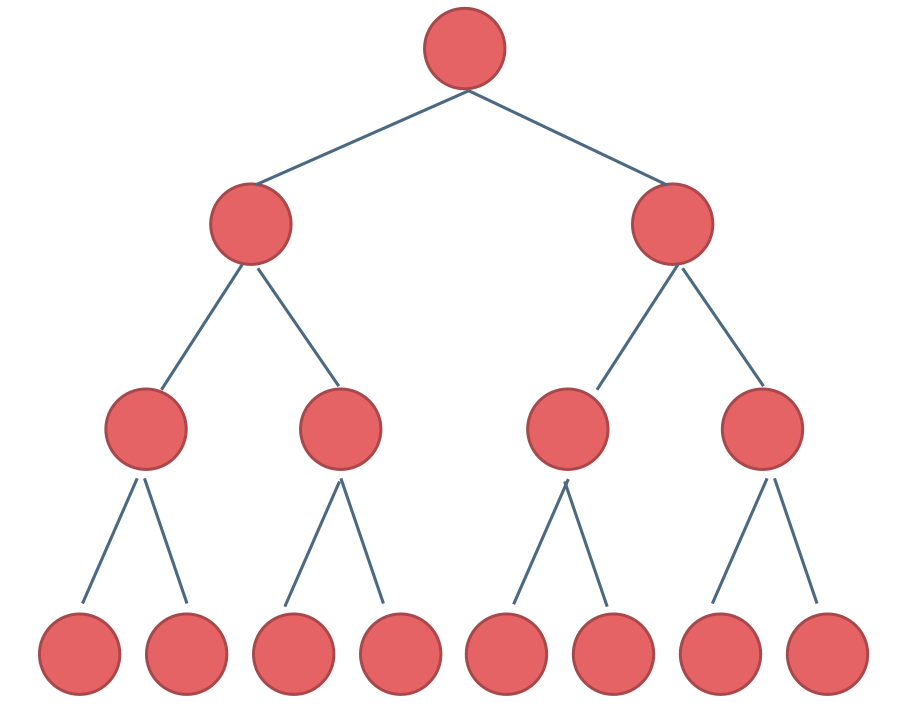
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。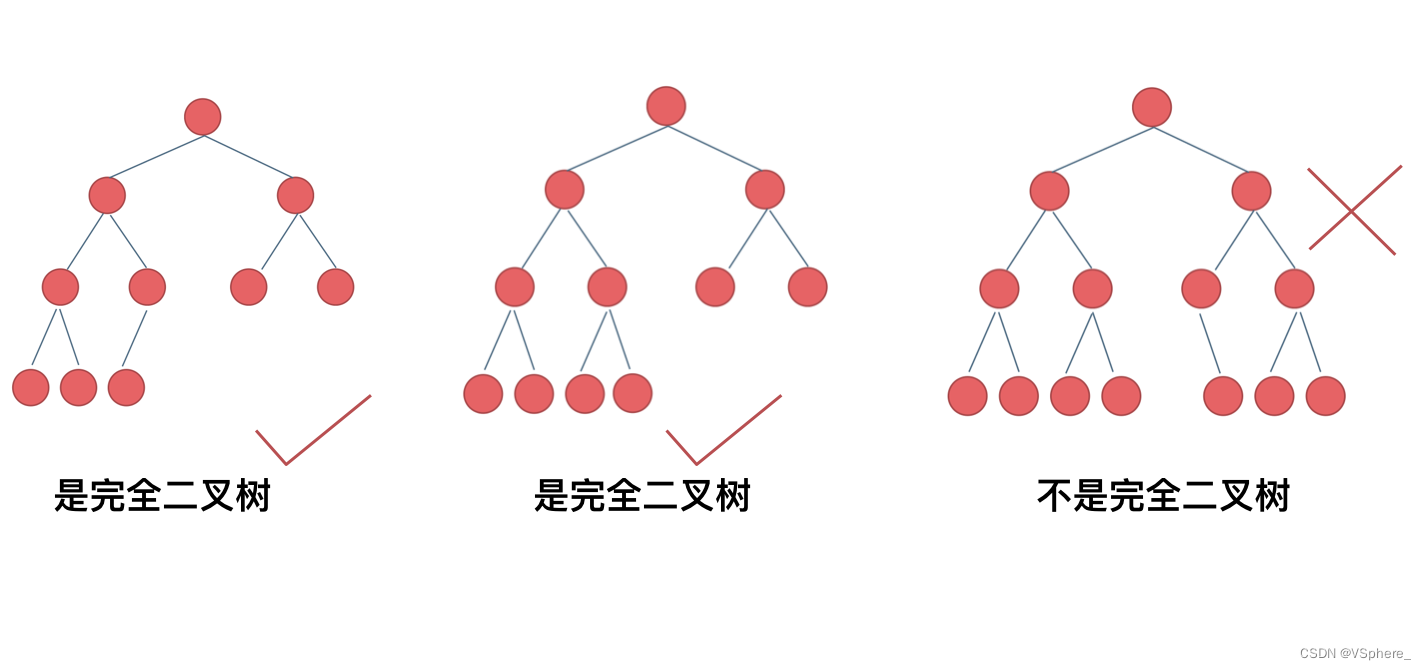

 

优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树

二叉搜索树是有数值的了，二叉搜索树是一个有序树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

• 它的左、右子树也分别为二叉排序树

下面两幅图所表示树就是二叉搜索树：

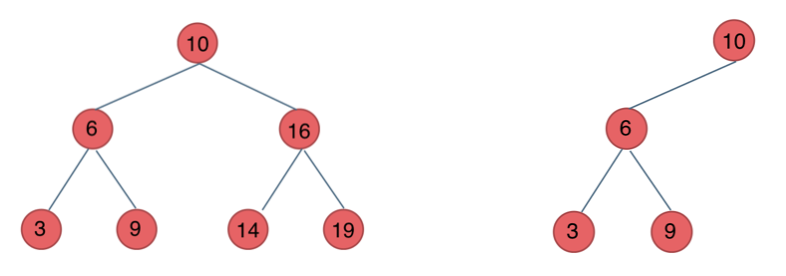
平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。如图：

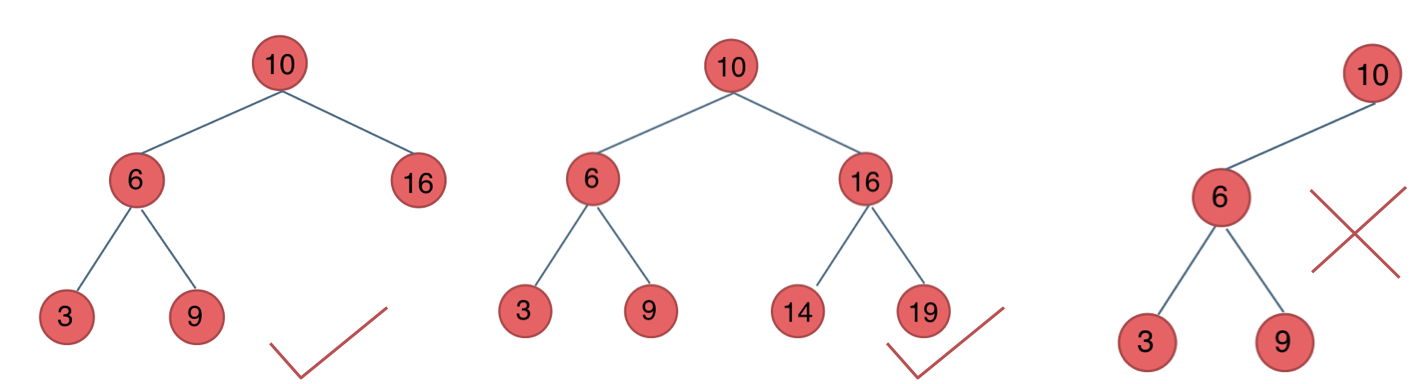
最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_map底层实现是哈希表。

二叉树遍历方式

二叉树主要有两种遍历方式：

1：深度优先遍历：先往深走，遇到叶子节点再往回走。

2：广度优先遍历：一层一层的去遍历。

从深度优先和广度优先的进一步拓展得到下面几种遍历方式

• 二叉树深度优先遍历

1. 前序遍历

2. 中序遍历

3. 后序遍历

• 二叉树广度优先遍历

层次遍历

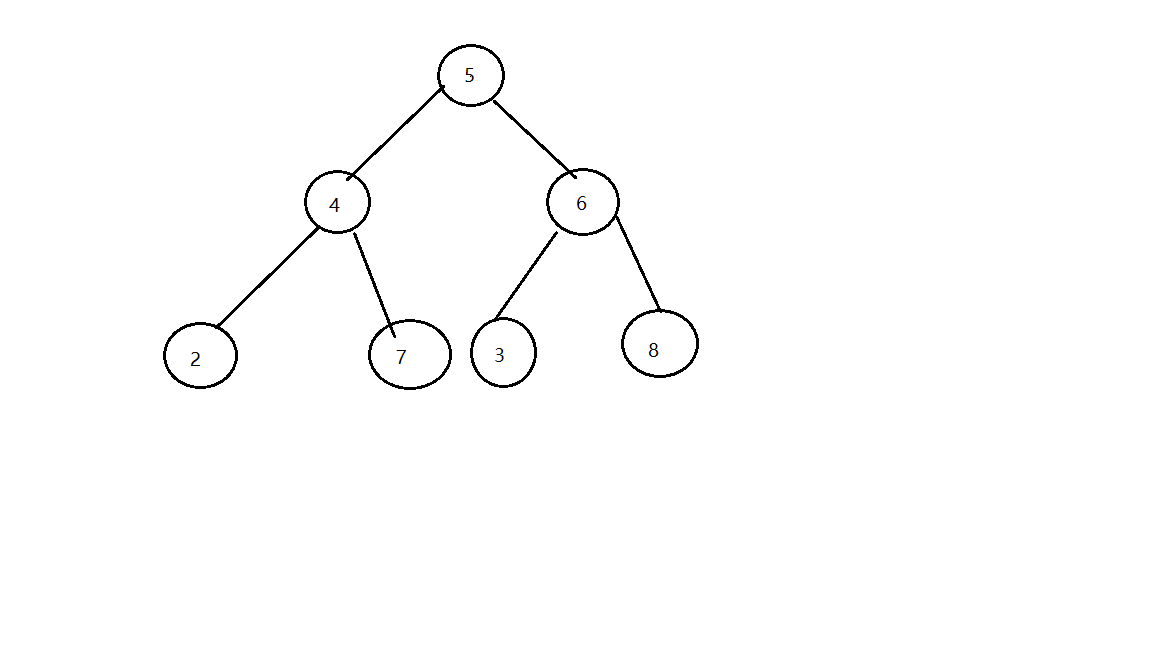
注：有些人容易将深度优先的三种遍历方式弄混淆，其实我们只要记住一个小技巧就好，所谓的前中后序遍历，其实指的就是中间节点的遍历顺序，我们把前中后看成中间结点的位置就好了

如上图遍历顺序如下：

前序遍历（根左右）：5427638.

中序遍历（左根右）：2475368.

后序遍历（左右根）：2743865.

层序遍历：5462738.