原文名称为:《Multiple lookup table predistortion for adaptive modulation》
摘要
本文提出了一种基于Hammerstein模型的多LUT数字自适应预失真器,该模型使用返回通道从接收器反馈信息,具体来说是误码率(bit error rate,BER),以便训练并随后调整特定的LUT增益,从而始终以最佳状态工作水平。这种新的预失真器结构旨在处理使用自适应调制的现代通信标准(例如IEEE802.11或IEEE802.16),因此在保证一定的接收服务质量的同时,不断地搜索最佳线性放大器以最大化功率效率。仿真结果表明了这种多查找表结构的优点,在不同信道条件下,在保证一定的接收误码率水平的同时,实现了线性高效放大。
I. Introduction
功率放大器(Power Amplifier ,PA)线性化是文献中广泛提出的一个众所周知的问题,但是它始终是开放的因为它必须不断地应对新的通信场景,在这些场景中,线性放大是必须的,而功率效率是一个重要的指标。 自从以前的中波和短波无线电发射机以来,已经提出了许多线性化技术[1],并取得了重大进展[2]。 当前高速数字信号处理器(DSP)的使用不仅恢复了经典的模拟解决方案(例如Kahn的包络消除和恢复[EE&R]或Chireix的解决方案[3]),而且还促进了线性化问题的新解决方案。 几年前,由于成本和DSP能耗的原因,使用数字处理器对PA进行线性化被认为是一个不错的解决方案,但它不合理。目前,大多数通信设备已经集成了一些数字处理器,用于无线标准中的强制性问题(如编码、交织、OFDM等),也可以用来实现基于数字的线性化,而不需要专门用于这一功能的特定的数字器件。在所有的线化器中,文献中提出的一些基于数字的线化器有:使用非线性元件的线性放大(LINC,实际上是Chireix结构)[4]及其变体CAL-Lum,EE&R和RF,BB或IF数字预失真 。最近几年提出的大多数数字预失真器都是用无记忆技术建模的。对于窄带信号(例如几乎恒定的包络调制),此PA无记忆模型可能是可以接受的近似值。 但是,由于新的多级调制格式要求功率处理能力和更高的基带带宽,无记忆预失真已经显示出不足的存储性能。
因此,对于当前的宽带多电平调制格式,有必要考虑功放存储模型,所提出的用作存储预失真器件的模型通常基于Volterra级数(或剪枝Volterra)[5,6]、存储多项式[7]、Wienner-Hammerstein模型[8]或神经网络[9],当前的通信标准,如ASIEEE802.11g、IEEE802.16、ETSIHiperlan-2、UMTS或ETSIDVB,通过使用多电平调制、多载波或组合两者(例如M-QAM、π/4DQPSK、WCDMA、单载波或OFDM),在中等信道带宽(超过20MHz)上寻找高频谱效率。
这些调制方案在幅度和相位上都有信息,因此对PA非线性非常敏感。 考虑到它们呈现出较高的峰均功率比(PAPR),因此线性放大需要显着的补偿水平,从而降低了PA的功率效率。 为了保证功率放大中的最大功率效率,本文提出了一种基于Hammerstein模型的LUT数字自适应预失真器(考虑了记忆效应)。在文献[10]中提出了使用多个查找表对功放特性短期变化的数字预失真进行数字预失真的优点。
本文提出的预失真器架构利用来自接收机的误码率(BER)信息(通过大多数现代无线标准规定的返回信道)为每个调制设计两个特定的LUT,提供异常和安全模式操作。因此,该架构允许在实现接收中的特定服务质量(QoS)时设置最佳操作补偿水平。
与以前的数字预失真器建议[5-11]相比,这种基于多LUT的预失真器通过自适应地计算最佳PA +预失真器增益,以尽可能接近饱和的方式工作,从而最大程度地提高效率,从而解决了应对不同调制格式的问题。
II. Problem statement
由于某些现代通信标准允许自适应调制,即根据信道条件更改调制格式,因此线性放大将考虑使用不同的PAPR。 输入退避可以定义为如[11]所示:
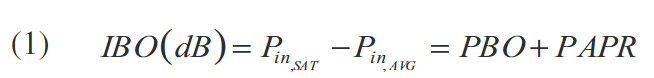
其中Pin,SATP_{in,_{SAT}}Pin,SAT表示对应于输出饱和功率的输入功率,Pin,AVGP_{in,_{AVG}}Pin,AVG表示输入平均功率电平,PBO表示峰值补偿,其定义为:
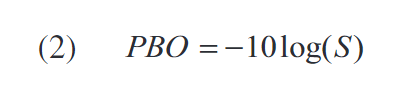
S是饱和功率的分数(介于0到1之间的值),考虑该分数是为了定义馈送在功放输入端以获得线性放大的最大输入功率:
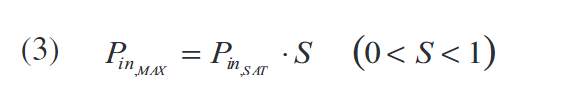
因此,考虑到使用不同调制格式呈现不同PAPR的通信发射机,考虑到随时使用的特定调制来调整PA的输入补偿是合理的。
为了调整最佳补偿,可以:–改变每个调制的输入平均功率电平调制格式然后,将需要某种附加的功率控制;
–或者,请参见等式。 (1)保持固定的平均输入功率,改变由预失真器和PA组成的整体链增益,从而改变饱和功率电平。
因此,如图1所示,可以通过调整总体预失真器+PA增益来设置输入回退电平。 此外,如图1所示,多级调制载波仅偶尔达到峰值包络功率(PEP)。
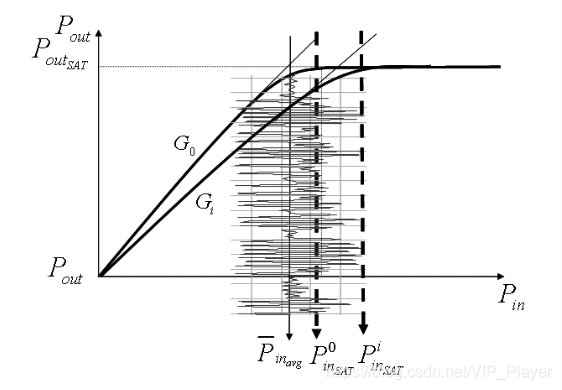
图1.考虑了不同放大增益的PA的AM-AM曲线
此外,如图1所示,多电平调制载波仅偶尔达到峰值包络功率(s peak envelope power,PEP)。大多数时候,调制载波的平均功率水平明显低于峰值包络功率(PEP)。 为了提供最高效率的放大,有时需要一定程度的信号限幅。因此,本文的目标是提出一种能够找到最佳补偿电平的自适应预失真器,以获得功率有效放大,并在接收时保持特定的误码率。
III. Predistortion model 预失真模型
尽管Volterra级数是具有记忆的通用非线性模型,但其预失真很复杂,并且难以实时实现。 除了更复杂的模型(例如神经网络)以外,还有两种简单但有效的可能性来描述考虑了记忆效应的预失真模型。 这些是记忆多项式或Hammerstein(Wiener)模型。但是,记忆多项式可以看作是更一般的Hammerstein模型的特殊配置。
A) Hammerstein model
Hammerstein模型由无记忆非线性和线性时不变系统组成,如图2所示。而Wiener模型由相同的子系统组成,但顺序相反。基于Hammerstein模型的预失真器既可以补偿功放的非线性(通过无记忆非线性块),也可以补偿功放的频率依赖特性(通过线性时不变系统)。在线性时不变块中使用FIR滤波器将对应于记忆多项式模型,如公式(4)中所述:

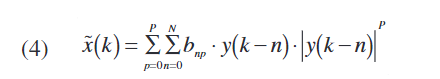
其中y(n)和x~(n)\tilde{x}(n)x~(n)是预失真器模型的输入和输出信号,而bnp[N=1...N;p=1...P]b_{np} [N=1...N;p=1...P]bnp[N=1...N;p=1...P]是复数增益,N和P分别是模型中考虑的延迟数和非线性阶数。
在本文中,我们考虑了在线性时不变块中使用IIR滤波器,因为在相同的滤波器阶数下,IIR滤波器比FIR滤波器具有更好的分辨率,因此可以减少DSP中的计算量
B)Indirect learning of the predistorter 间接学习预失真器
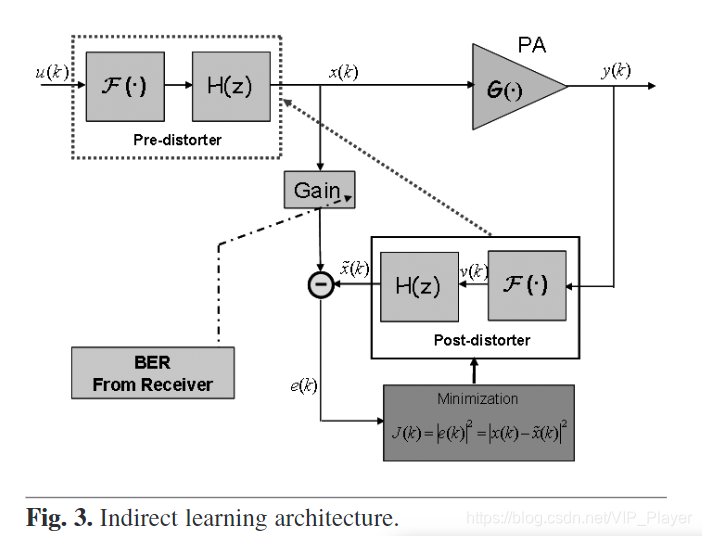
图3间接学习架构
为了识别Hammerstein模型参数,最常见的解决方案是使用间接学习结构(也称为转换方法[12]),如图3所示。在第一步中,通过使用PA输出信号和PA输入信号乘以特定线性增益(见图1的PAPR)来识别后失真参数,其值将与输入信号的PAPR相关,从而与其调制方案相关。等式 (5)显示了从功率放大器和后失真器的级联连接得到的线性放大结果:
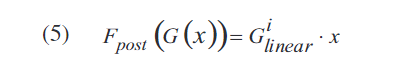
一旦估计出后失真系数,后失真器的一个有效拷贝将与PA级联,从而得到预失真器。
通过观察图3中的框图,可以通过以下等式定义后失真器(predistorter)学习过程:
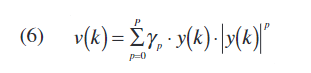
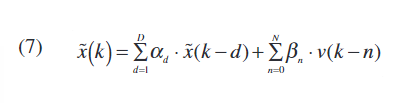
y(K)为PA输出,v(K)为Hammerstein模型的无记忆非线性块的输出。P是无记忆多项式的阶数,N和D分别是一般的零/极点阶数。
通过结合等式 (6)和(7)我们得到预失真器输入输出的闭合表达式:
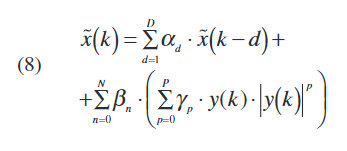
重写等式 (8)以更紧凑的矩阵表示法得出:
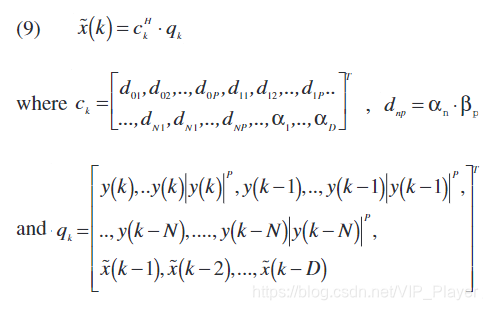
其中向量用粗体表示,矩阵用粗体和帽子表示。超指数H表示Hermitian转置。
IV. Identification algorithms识别算法
为了估计后失真系数,将最小化的成本函数(J(K))定义为后失真的输出样本与PA的输入样本(先前乘以期望的线性增益)之间的均方误差,如公式(10)所示
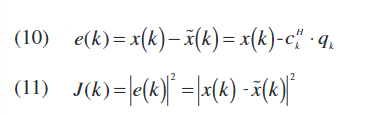
为了最小化此成本函数,提出了两种算法:最小均方(LMS)算法和快速卡尔曼滤波器。 其他算法(例如LeastSquares或递归最小二乘)适用于训练预失真器,但会导致PA特性前端意外变化的自适应过程产生更多的计算复杂性。
A) Least Mean Square (LMS)
(12)等式中描述了众所周知的最小均方算法。
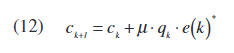
m是误差步长(收敛速度和准确性之间的权衡),其界限是:
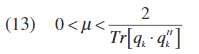
其中Tr[·]表示数据(信号)矩阵的迹线。
B) Fast-Kalman Filter
快速卡尔曼算法[13]使用最优卡尔曼滤波技术来自适应地估计前失真系数,而无需知道优先转换矩阵(与传统的卡尔曼滤波器不同)。 描述算法的Fast-Kalman方程为[13]:
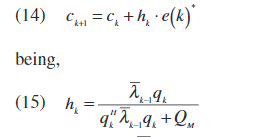
其中QM和与Qp估计和测量误差方差有关[13]。 λk为递归更新矩阵,如下所示:
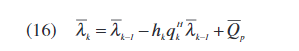
C) Look-up table (LUT) coefficients
由于实时自适应算法将需要能够在符号周期内计算复杂算法的高速DSP,因此使用预训练的查找表可以简化DSP的计算负荷并放宽自适应时间常数。 因此,基于Hammerstein的预失真器的一种可能的实现将包括使用LUT来补偿PA的无记忆非线性,然后是IIR滤波器(见图4),以补偿由于热效应而产生的可能的记忆效应。
但是,为了将预失真器分解为查找表加IIR滤波器,首先需要分别得到Hammerstein参数。
看一下等式(12)和/或等式(14)可能注意到使用LMS或Fast-Kalman算法如何获得ck系数矢量,其中
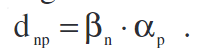
为了分别识别伽玛和贝塔,有可能应用Bai在[14]中提出的两阶段识别算法,包括等式中描述的矩阵的奇异值分解。 (17)。
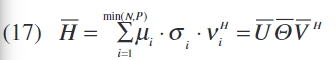
matrix is defined as:
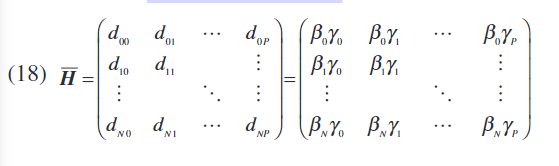 作为矩阵
作为矩阵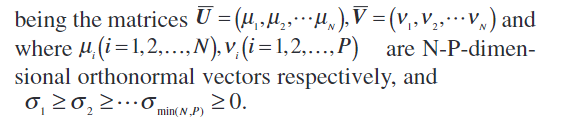
N-P分别是空间正交的
最后,如等式中所述估计伽玛和贝塔。 (19)和等式 (20)。
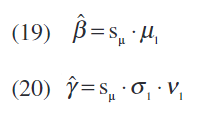
其中sus_usu表示μ1μ_1μ1的第一个非零元素的符号。
或者,通过使用纳伦德拉-加尔曼(Narendra-Gallman)算法[15],基于借助于最小二乘技术的预失真器系数的估计,可以分别获得α、β和γ系数。NG算法可以很好地用于综合训练过程中的多个查找表,但对于以后的自适应,LMS或快速卡尔曼算法更适合,因为它们更简单、更快。
V. Multiple lookup tables
基于多LUT的预失真器的方框图如图4所示。它由一组2×Q LUT和它们相关的IIR滤波器组成,Q是所考虑的调制方案的数量。 每个调制格式已分配了两个具有不同增益的LUT,即正常增益和安全模式增益,以及它们对应的滤波器。 这组LUT的目的是补偿PA非线性行为,而IIR滤波器则用于补偿PA记忆效应。
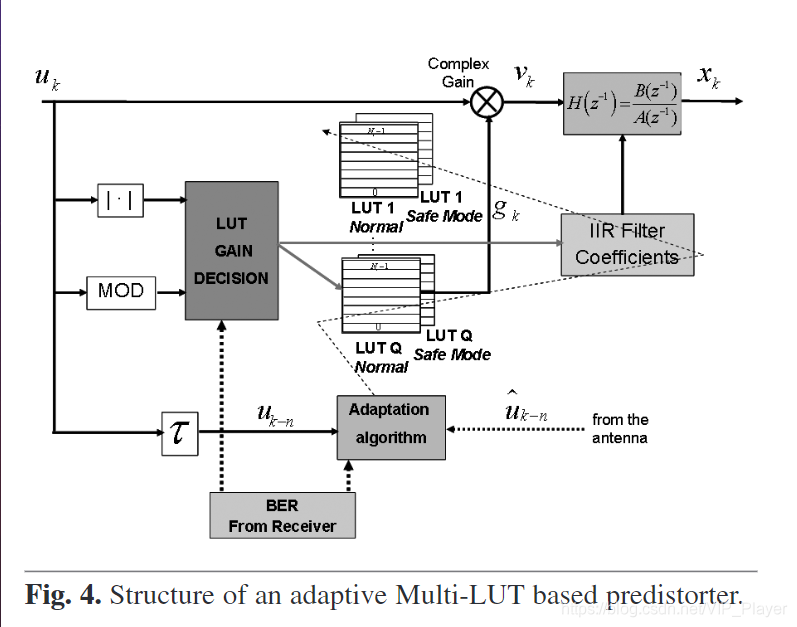
图4.基于多查找表的自适应预失真器结构
正常增益LUT具有最小的必要补偿,可以在接收时完成BER规范,因此,其目标是始终在最有效的动态范围内工作。 安全模式增益LUT提供了显着的补偿操作,以补偿PA特性或信道条件的任何下降。
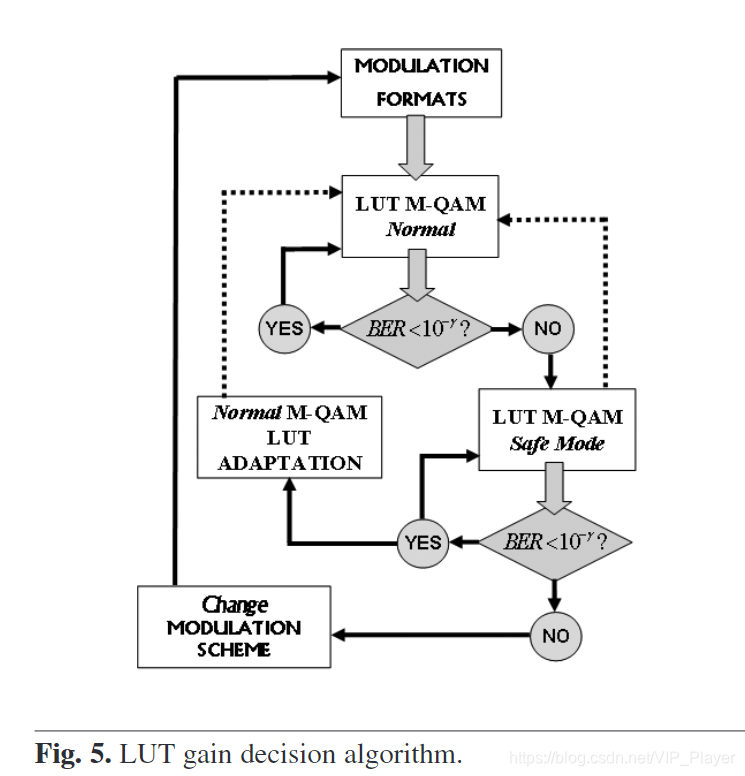
图4中的“ LUT增益决策(LUT Gain Decision)””块执行图5中描述的LUT增益决策算法。第一步,考虑到输入信号的调制格式,分配了一个正常增益LUT(及其相应的滤波器) 。 如果不能保证接收时所需的最小BER(BER> 10–γ10^{–γ}10–γ),LUT增益判决切换到安全模式增益LUT。 然后,如果达到了最小BER,则以并行方式(在不同的时间范围内)开始正常增益LUT的自适应过程,以便重新调整PA特性中遭受的任何可能变化。但是,如果在安全模式增益LUT下操作,则在接收时没有达到所需的误码率,这意味着功放的非线性行为不会像信道条件那样对误码率降低有那么大的贡献。 因此,发射机必须选择更稳健的调制格式。
VI. Experimental results
A) Power amplifier model characterization 功率放大器模型特性
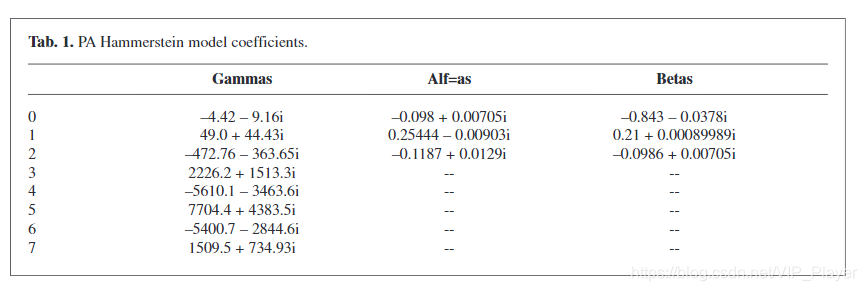
对于实验结果,我们考虑了一个PA Hammerstein模型,该模型是根据使用Agilent ATF-54143 PHEMT晶体管设计的APA类的调制输入和输出数据估算的。 表1列出了获得的系数,其静态AM-AM曲线如图6所示。
B)训练过程:计算多LUT增益
在训练过程中,考虑了四种不同类型的调制方案(均为IEEE802.16标准所支持的调制方案):QPSK、16QAM、64QAM和256QAM(均为灰度星座排序),这些调制方案均由滚降因子为α=0.35时的根升余弦滤波器滤波。在训练过程中,考虑了四种不同类型的调制方案(均为IEEE802.16标准所支持的调制方案):QPSK、16QAM、64QAM和256QAM(均为灰度星座排序),这些调制方案均由滚降因子为α=0.35时的根升余弦滤波器滤波。通信信道是信噪比为10dB的加性高斯白噪声信道,不考虑多径和多普勒,假设整个系统自适应50Ω,则1dB压缩点(见图6)将大致对应于0.75Vrms的输入幅度,即7.5dBm的输入功率,而输出饱和功率约为23dBm(对应于4.5Vrms)。考虑的调制的PAPR可以使用等式 (21)计算。:
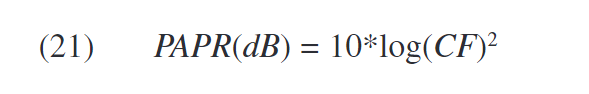
如上所述,作为峰值因子(CF)的信号的峰值与r.m.s采样的比率。
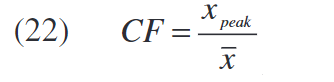
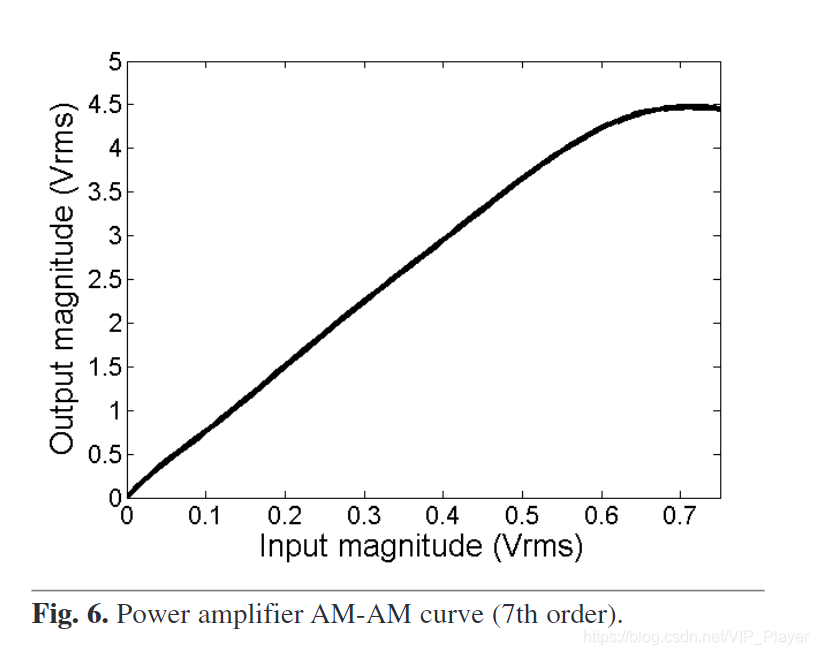
图6.功率放大器AM-AM曲线(7阶).
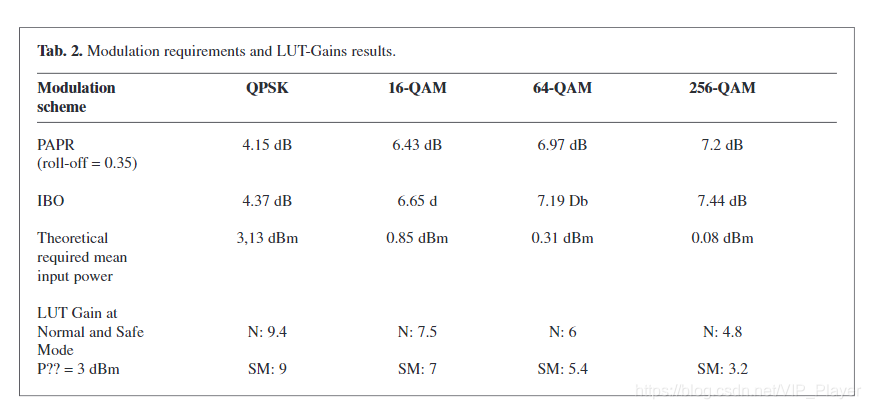
对于我们的特定功率放大器,输入饱和功率为7.5 dBm,并考虑到饱和功率S = 0.95的分数(请参见等式(1),(2)和(3))如果PBO的峰值补偿为0.22 dB,则最大输入功率设置为7.13dBm。 因此,考虑到限制性最强的PAPR(属于256 QAM调制,请参见表2)并使用等式(1),线性扩增的最低推荐IBO为IBO≥7.5db。 但是,通过使用Multi-LUT预失真,平均输入功率固定为3 dBm,因此,与调制方式无关,考虑IBO = 4.5 db的一般IBO。
PBO : peak back-off,峰值补偿
IBO :input back-off 输入补偿
为了在接收时达到BER规范,必须提前计算所有正常和安全模式增益LUT及其相应的滤波器。 图7显示了针对不同输入LUT增益和不同调制方案的误码率,其中包括3 dBm的输入平均功率,SNR = 10 dB的AWGN信道和128个条目的LUT。
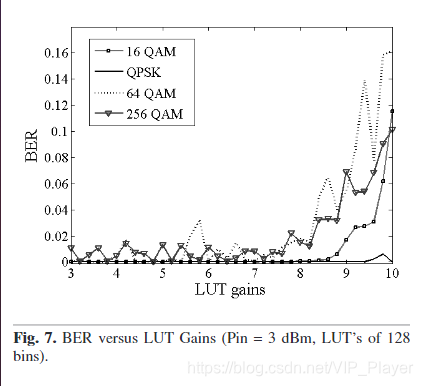
图7. BER与LUT增益(引脚= 3 dBm,LUT为128bins)
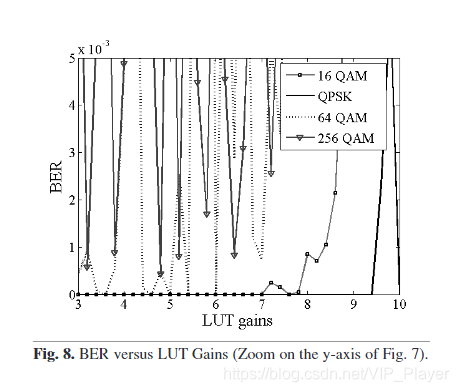
考虑到BER <10–3(在包含编码增益之前)的BER限制并观察图8(图7的放大图),表2列出了每种调制的LUT增益。
C)正常流程
图9显示了AWGN信道的不同SNR的BER和不同的调制格式。调制8和7对应于256 QAM正常和安全模式增益LUT。 调制6和5对应于64 QAM; 4和3至16 QAM; 最后,分别为QPSK的正常模式和安全模式的2和1增益LUT。如图9所示,可以识别图5中描述的LUT决策算法。直到可以有效放大之前,正常增益LUTi都是首选,但是当信道条件变得更糟时 ,如果安全模式增益LUT不够,则更改调制格式。 请注意,自适应后,算法将以更有效的放大(或调制格式,如果适用)重试。
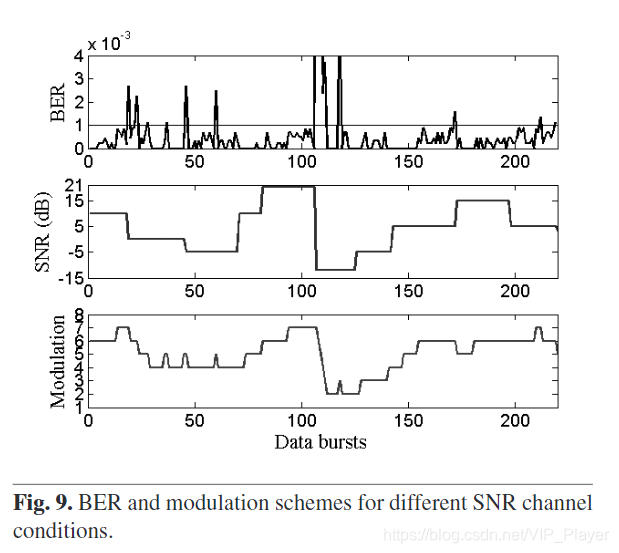
图9.不同SNR信道条件的BER和调制方案。
VII. Conclusion
本文提出了一种多LUT数字自适应预失真器,该预失真器能够同时支持不同的调制格式,并通过在接收机处反馈BER信息来确保高效的线性放大。 文中给出了设计过程和基本原理,并给出了仿真结果,证明了其良好的性能。在不同的模型参数辨识方案中,考虑了计算量较小的方案,目的是在现代通信系统中已有的DSP基础设施上建立预失真器算法,从而最大限度地减少对其它DSP功能的干扰。这种多LUT预失真器的主要优点在于,即使将动态范围调整到最佳补偿水平,也不会对放大增益造成不利影响,因为在接收允许的情况下,它始终会像指定的BER一样接近饱和。





 本文介绍了一种基于Hammerstein模型的数字自适应预失真器,用于处理使用自适应调制的现代通信标准。该预失真器利用返回通道的误码率信息来训练和调整LUT增益,以实现线性高效放大,同时保证接收质量。通过仿真,验证了多查找表结构在不同信道条件下的优势。
本文介绍了一种基于Hammerstein模型的数字自适应预失真器,用于处理使用自适应调制的现代通信标准。该预失真器利用返回通道的误码率信息来训练和调整LUT增益,以实现线性高效放大,同时保证接收质量。通过仿真,验证了多查找表结构在不同信道条件下的优势。
















 143
143

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








