变色:结点的颜色由红变黑或由黑变红。
红黑树的查找也不说了,它是二叉树,所以二叉树怎么查找,红黑树就怎么查找。
插入节点
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
第二步:将插入的节点着色为"红色"。为什么是红色?你猜啊
(看一下性质五)
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
第二步中,将插入节点着色为"红色"之后,不会违背"特性(5)"。那它到底会违背哪些特性呢?
很显然,只有性质4.(每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点))比较危险。
那接下来,想办法使之"满足性质4. ",就可以将树重新构造成红黑树了。
昨天我躺在床上,辗转反侧,梦中顿悟,红黑树插入会有以下这么几种情况:
1、被插入的节点是根节点。
那最好办,那说明是空树,直接涂黑就好。
2、新插入节点的父节点是黑的(新插入的节点,不会有子节点存在,这个可以放心)
这个更好办,就插入就完了
3、新插入节点的父节点是红的
那就有意思了。具体情况下面讨论
对于上面第三种情况的再分析:
1、新节点的父节点的兄弟节点是红的
//以下两种情况默认包含了父节点没有兄弟的情况
2、新节点的父节点的兄弟节点是黑的,且当前节点是其父节点的 右 孩子
3、新节点的父节点的兄弟节点是黑的,且当前节点是其父节点的 左 孩子
(为什么要这样分?不急慢慢看,我也纳闷儿呢!!!)
上面三种情况处理问题的核心思路都是:将红色的节点移到根节点;然后,将根节点设为黑色。下面对它们详细进行介绍。
情况一:
策略:
(01) 将“父节点”设为黑色。
(02) 将“叔叔节点”设为黑色。
(03) 将“祖父节点”设为“红色”。
(04) 将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作。
这里需要说明一下,当祖父节点被染红,它可能会和它自己的父节点起冲突,所以需要向上递归。
就碧如这样:
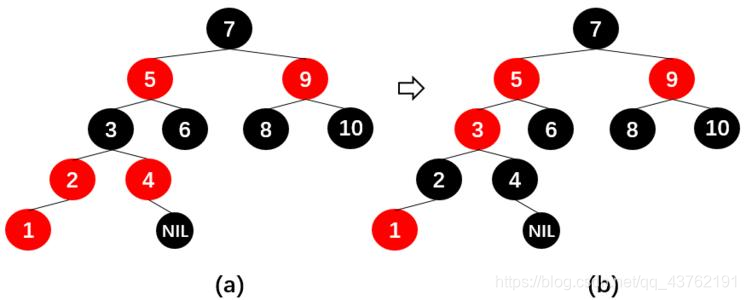
为什么采用这个策略?
“当前节点”和“父节点”都是红色,违背“性质4. ”。所以,将“父节点”设置“黑色”以解决这个问题。
但是,将“父节点”由“红色”变成“黑色”之后,违背了“性质5. ”:因为,包含“父节点”的分支的黑色节点的总数增加了1。
解决这个问题的办法是:将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”。
这里为什么要将“叔叔节点”也变黑?思考思考,不难理解的。
理解不了的话对着上面那张图去数性质5.
这里需要再说明一下,当祖父节点被染红,它可能会和它自己的父节点起冲突,所以需要向上递归。
情况二:
策略:
(01) 将“父节点”作为“新的当前节点”。
(02) 以“新的当前节点”为支点进行左旋。
草率了。。。
哎,看图吧:
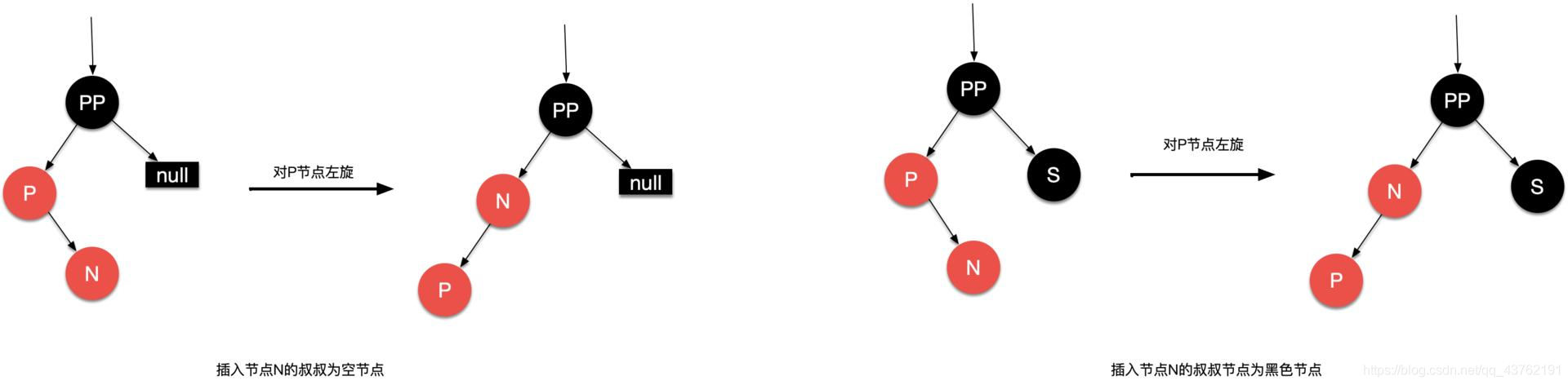
呐,弄完之后,变成了第三种情况了。
情况三:
策略:
(01) 将“父节点”设为“黑色”。
(02) 将“祖父节点”设为“红色”。
(03) 以“祖父节点”为支点进行右旋。
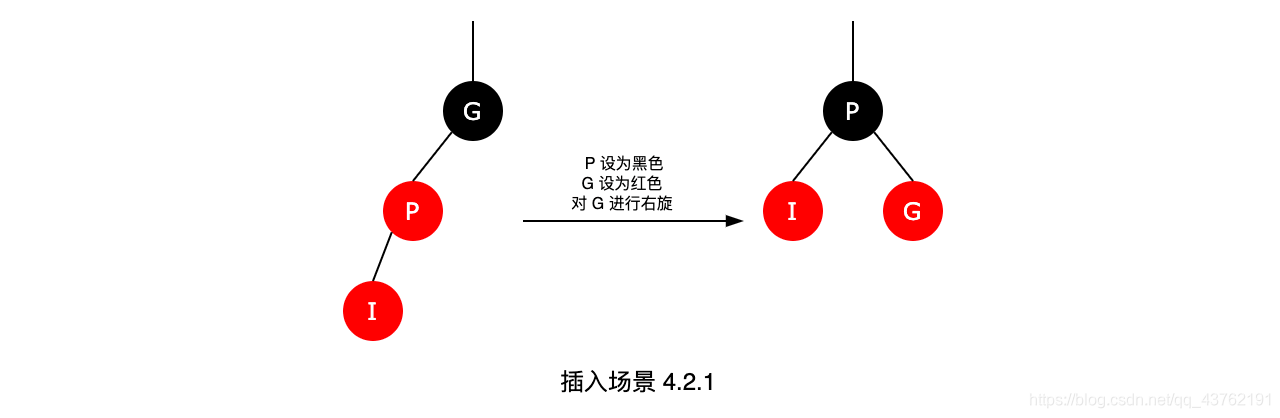
为什么采用这个策略?
为了便于说明,我们设置“当前节点”为S(Original Son),“兄弟节点”为B(Brother),“叔叔节点”为U(Uncle),“父节点”为F(Father),祖父节点为G(Grand-Father)。
S和F都是红色,违背了红黑树的“性质4. ”,我们可以将F由“红色”变为“黑色”,就解决了“违背‘性质4. ’”的问题;但却引起了其它问题:违背“性质5. ”,因为将F由红色改为黑色之后,所有经过F的分支的黑色节点的个数增加了1。那我们如何解决“所有经过F的分支的黑色节点的个数增加了1”的问题呢? 我们可以通过“将G由黑色变成红色”,同时“以G为支点进行右旋”来解决。
对于红黑树的节点插入,我讲明白了吗?
关注点赞收藏,我们继续往下。
删除节点
相较于插入操作,红黑树的删除操作则要更为复杂一些。删除操作首先要确定待删除节点有几个孩子,如果有两个孩子,不能直接删除该节点。而是要先找到该节点的前驱(该节点左子树中最大的节点)或者后继(该节点右子树中最小的节点),然后将前驱或者后继的值复制到要删除的节点中,最后再将前驱或后继删除。
第一步:将红黑树当作一颗二叉查找树,将节点删除。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
在第一步中"将红黑树当作一颗二叉查找树,将节点删除"后,可能违反"性质(2)、(4)、(5)"三个性质。第二步需要解决上面的三个问题,进而保持红黑树的全部特性。
删除一个红色节点,并不会有什么不适。
所以我们将目光聚焦在删除一个黑色节点上。
删除一个节点有以下四种情况:
1.删除的节点没有孩子
2.删除的节点只有左子树
3.删除的节点只有右子树
*4.删除的节点拥有左子树和右子树
其实只有上面前三种情况,对于第四种情况,可以找到待删除节点的直接后继节点,用这个节点的值替代待删除节点,接着情况转变为删除这个直接后继节点,情况也变为前三种之一。(前驱和后继至多只有一个孩子节点)
1.删除的节点只有左子树或只有右子树:
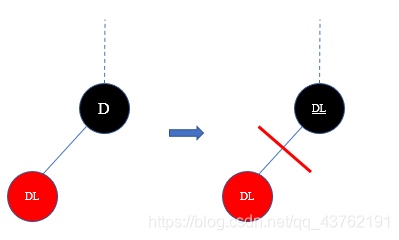
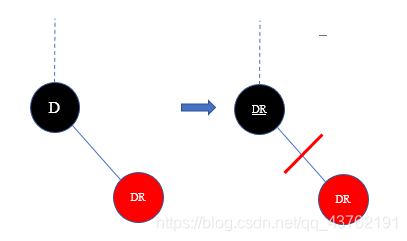
2.删除的节点没有孩子
1)待删除节点是红色的,直接删去这个节点。
2)父节点P是红色节点
解决方案:把P节点染成黑色,兄弟节点染成红色,删除节点D。
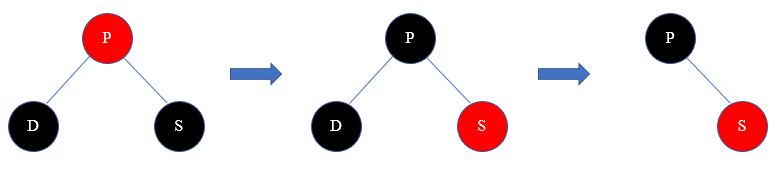
3)兄弟节点S是红色节点
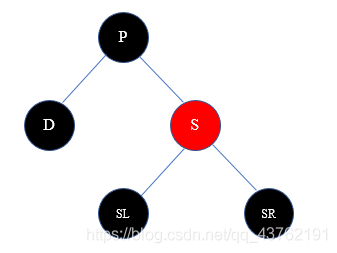
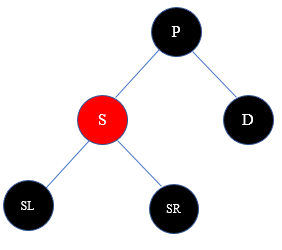
解决方案:把P染成红色,S染成黑色,然后以P为轴做相应的旋转操作(D为P的左子树则左旋,否则右旋)
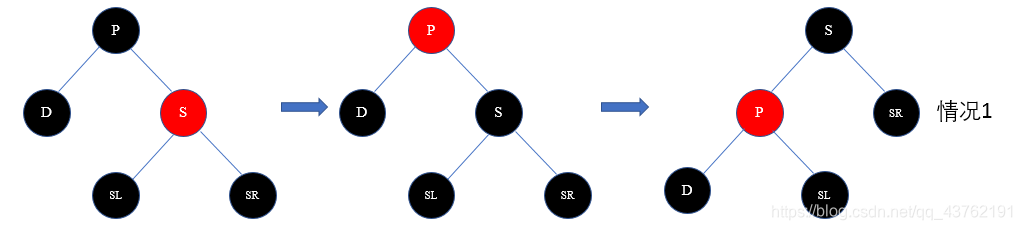
4)节点D的远亲侄子为红色节点的情况(父节点P可红可黑)
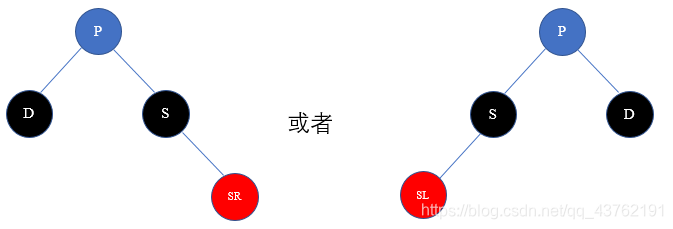
解决方案:交换P和S的颜色,然后把远亲侄子节点SR/SL设置为黑色,再已P为轴做相应的旋转操作(D为P的左子树则左旋,否则右旋),删除节点D。

5)节点D的近亲侄子为红色节点的情况(父节点P可红可黑)

解决方案:把S染成红色,把近亲侄子节点SR/SL染成黑色,然后以节点S为轴做相应的旋转操作(D为P的左子树则右旋,否则左旋),变成了情况4,按照情况4进行操作。
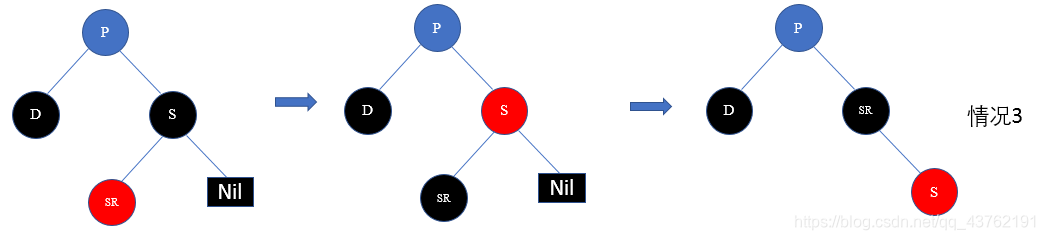
6)节点D,P,S均为黑色节点

解决方案:把D删去,然后把节点S染成红色。
①从节点P往上依然是全黑的情况

②从节点P往上是其他情况

#include
using namespace std;
class RB_tree{
//还得去重载一下这个 “=”
public:
RB_tree():
RB_tree(int x, bool color) : val(x),color(color), left(NULL), right(NULL) {}
//寻找插入位置,并插入
RB_tree search_and_insert(RB_tree* head, int val){
/*
副函数,没别的意思,就是觉得全堆在一个函数里不好看
*/
RB_tree* node = head;
while(1){
if(val>node->val){
if(node->right){
node = node->right;
}
else{
node->right = new RB_tree(val, 0);
node->right->parent = node;
node = node->right;
return node;
}
}
else{
if(node->left){
node = node->left;
}
else{
node->left = new RB_tree(val, 0);
node->left->parent = node;
node = node->left;
return node;
}
}
}
}
RB_tree* adopt(RB_tree* node_now){
//开始调整
RB_tree* parent_node = node_now->parent; // 目前节点的父节点
if(!parent_node->color){ // #3
/*
父红,子红,开始分
3.1、父没有兄弟节点
将父节点调黑,祖父节点调红,一字则左/右旋,之字先旋转成为一字
3.2、父有兄弟节点
3.2.1 父的兄弟节点是红的
直接把父节点染黑,父的兄弟节点也染黑,父的父节点染红
父的父节点成为当前节点
3.2.2 父的兄弟节点是黑的,这不可能,它有个屁的兄弟节点啊,性质5不允许它有兄弟
*/
if(parent_node == parent_node->parent->left){ //如果父节点是祖父节点的左子节点, 后面旋转的时候也用得上
if(NULL == parent_node->parent->right){ // #3.1
parent_node->parent->color = 0;
if(parent_node->parent->parent->left == parent_node->parent){
if(node_now == parent_node->right){
parent_node->color = 1;
parent_node->parent->parent->left = LL(parent_node->parent);
}
else{
node_now->color = 1;
parent_node->parent->parent->left = RL(parent_node->parent);
}
}
else{
if(node_now == parent_node->right){
parent_node->color = 1;
parent_node->parent->parent->right = LL(parent_node->parent);
}
else{
node_now->color = 1;
parent_node->parent->parent->right = RL(parent_node->parent);
}
}
}
else{ // #3.2
parent_node->color = 1;
parent_node->parent->right->color = 1;
return adopt(parent_node->parent);
}
}
else{
if(NULL == parent_node->parent->left){ // #3.1
parent_node->parent->color = 0;
if(parent_node->parent->parent->left == parent_node->parent){
if(node_now == parent_node->left){
parent_node->color = 1;
parent_node->parent->parent->left = RR(parent_node->parent);
}
else{
node_now->color = 1;
parent_node->parent->parent->left = LR(parent_node->parent);
}
}
else{
if(node_now == parent_node->left){
parent_node->color = 1;
parent_node->parent->parent->right = RR(parent_node->parent);
}
else{
node_now->color = 1;
parent_node->parent->parent->right = LR(parent_node->parent);
}
}
}
else{ // #3.2
parent_node->color = 1;
parent_node->parent->left->color = 1;
return adopt(parent_node->parent);
}
}
}
return head; // #2
}
//插入新节点
RB_tree* insert_node(RB_tree* head,int val){
/*
1、如果头结点是空的
2、如果插入节点的父节点的颜色是黑的
3、如果插入节点的父节点的颜色是红的
*/
if(NULL == head){ // #1
head = new RB_tree(val, 1);
return head;
}
else{
RB_tree* node = search_and_insert(head, val);
return adopt(node);
}
}
//找到要删除的节点,并返回
RB_tree* search_and_delete(RB_tree* head, int val){
}
//删除节点
RB_tree* delete_node(RB_tree* head, int val){
RB_tree* node = search(head, val);
/*
1、如果被删除的节点是红色节点,直接删除即可
2、如果被删除的节点是黑色节点,另当别论
*/
if(node->color == 0){
node->parent->left = node->right; //统一寻找后继
delete node;
node = NULL;
}
else{ //旋转玩记得删节点
/*
自我介绍一下,小编13年上海交大毕业,曾经在小公司待过,也去过华为、OPPO等大厂,18年进入阿里一直到现在。
深知大多数Java工程师,想要提升技能,往往是自己摸索成长或者是报班学习,但对于培训机构动则几千的学费,着实压力不小。自己不成体系的自学效果低效又漫长,而且极易碰到天花板技术停滞不前!
因此收集整理了一份《2024年Java开发全套学习资料》,初衷也很简单,就是希望能够帮助到想自学提升又不知道该从何学起的朋友,同时减轻大家的负担。
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,基本涵盖了95%以上Java开发知识点,真正体系化!
由于文件比较大,这里只是将部分目录截图出来,每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频,并且会持续更新!
如果你觉得这些内容对你有帮助,可以扫码获取!!(备注Java获取)

总结
在这里,由于面试中MySQL问的比较多,因此也就在此以MySQL为例为大家总结分享。但是你要学习的往往不止这一点,还有一些主流框架的使用,Spring源码的学习,Mybatis源码的学习等等都是需要掌握的,我也把这些知识点都整理起来了

《互联网大厂面试真题解析、进阶开发核心学习笔记、全套讲解视频、实战项目源码讲义》点击传送门即可获取!
能够帮助到想自学提升又不知道该从何学起的朋友,同时减轻大家的负担。**[外链图片转存中…(img-0bZcbOZ6-1713714927997)]
[外链图片转存中…(img-tFUfYoAZ-1713714927998)]
[外链图片转存中…(img-ebdOF9jh-1713714927998)]
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,基本涵盖了95%以上Java开发知识点,真正体系化!
由于文件比较大,这里只是将部分目录截图出来,每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频,并且会持续更新!
如果你觉得这些内容对你有帮助,可以扫码获取!!(备注Java获取)

总结
在这里,由于面试中MySQL问的比较多,因此也就在此以MySQL为例为大家总结分享。但是你要学习的往往不止这一点,还有一些主流框架的使用,Spring源码的学习,Mybatis源码的学习等等都是需要掌握的,我也把这些知识点都整理起来了
[外链图片转存中…(img-ZPqS2sC1-1713714927998)]
[外链图片转存中…(img-Md2nnFPb-1713714927998)]
《互联网大厂面试真题解析、进阶开发核心学习笔记、全套讲解视频、实战项目源码讲义》点击传送门即可获取!





















 1181
1181

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








