代码随想录算法训练营第 21 天 | 77. 组合、216. 组合总和 III、17. 电话号码的字母组合

原创 已于 2025-11-01 21:32:21 修改 · 660 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #java #数据结构

于 2025-10-31 00:26:56 首次发布

77. 组合

题目链接

易错点：

  1. startNumber 不是索引，就是实际的数，因为本题是 [1, n]，是从 1 开始的。
  2. 回溯时是 i + 1，不是startNumber + 1。

未剪枝；全局变量：

class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtrack(n, k, 1);
        return result;
    }

    public void backtrack(int n, int k, int startNumber) {
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startNumber; i <= n; i++) {
            path.add(i);
            backtrack(n, k, i + 1); // 注意这里是 i + 1，不是 startNumber + 1
            path.remove(path.size() - 1);
        }
    }
}

未剪枝；局部变量 -> 参数增多：

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<Integer> path = new ArrayList<>();
        List<List<Integer>> result = new ArrayList<>();        
        backtrack(n, k, 1, path, result);
        return result;
    }

    public void backtrack(int n, int k, int startNumber, List<Integer> path, List<List<Integer>> result) {
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startNumber; i <= n; i++) {
            path.add(i);
            backtrack(n, k, i + 1, path, result); // 注意这里是 i + 1，不是 startNumber + 1
            path.remove(path.size() - 1);
        }
    }
}

剪枝：

class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtrack(n, k, 1);
        return result;
    }

    public void backtrack(int n, int k, int startNumber) {
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startNumber; i <= n; i++) {
            // 剪枝
            if (path.size() + n - i + 1 < k) {
                break;
            }

            path.add(i);
            backtrack(n, k, i + 1); // 注意这里是 i + 1，不是 startNumber + 1
            path.remove(path.size() - 1);
        }
    }
}

216. 组合总和 III

题目链接

初始：有参数 sum

class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(k, n, 0, 1);
        return result;
    }

    public void backtrack(int k, int n, int sum, int startNum) {
        if (path.size() == k) {
            if (n == sum) {
                result.add(new ArrayList<>(path));
            }
            return;
        }
        for (int i = startNum; i <= 9; i++) {
            sum += i;
            path.add(i);
            backtrack(k, n, sum, i + 1);
            path.remove(path.size() - 1);
            sum -= i;
        }
    }
}

优化：用 n 减减来判断是否等于 0

class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(k, n, 1);
        return result;
    }

    public void backtrack(int k, int n, int startNum) {
        if (path.size() == k) {
            if (n == 0) {
                result.add(new ArrayList<>(path));
            }
            return;
        }
        for (int i = startNum; i <= 9; i++) {
            path.add(i);
            backtrack(k, n - i, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

剪枝：剪去 n 过小和元素数量不够了

class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(k, n, 1);
        return result;
    }

    public void backtrack(int k, int n, int startNum) {
        // 剪枝 1
        if (n < 0 || n > 45) { // 45 = 1 + 2 + ... + 9
            return;
        }


        if (path.size() == k) {
            if (n == 0) {
                result.add(new ArrayList<>(path));
            }
            return;
        }
        for (int i = startNum; i <= 9; i++) {
            if (path.size() + 9 - i + 1 < k) { // 剪枝 2
                return;
            }
            path.add(i);
            backtrack(k, n - i, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

17. 电话号码的字母组合

题目链接

树的深度由数字个数确定
树的宽度由字母表长度确定

index：digits 的下标，即树的深度
letters.length()：树的宽度

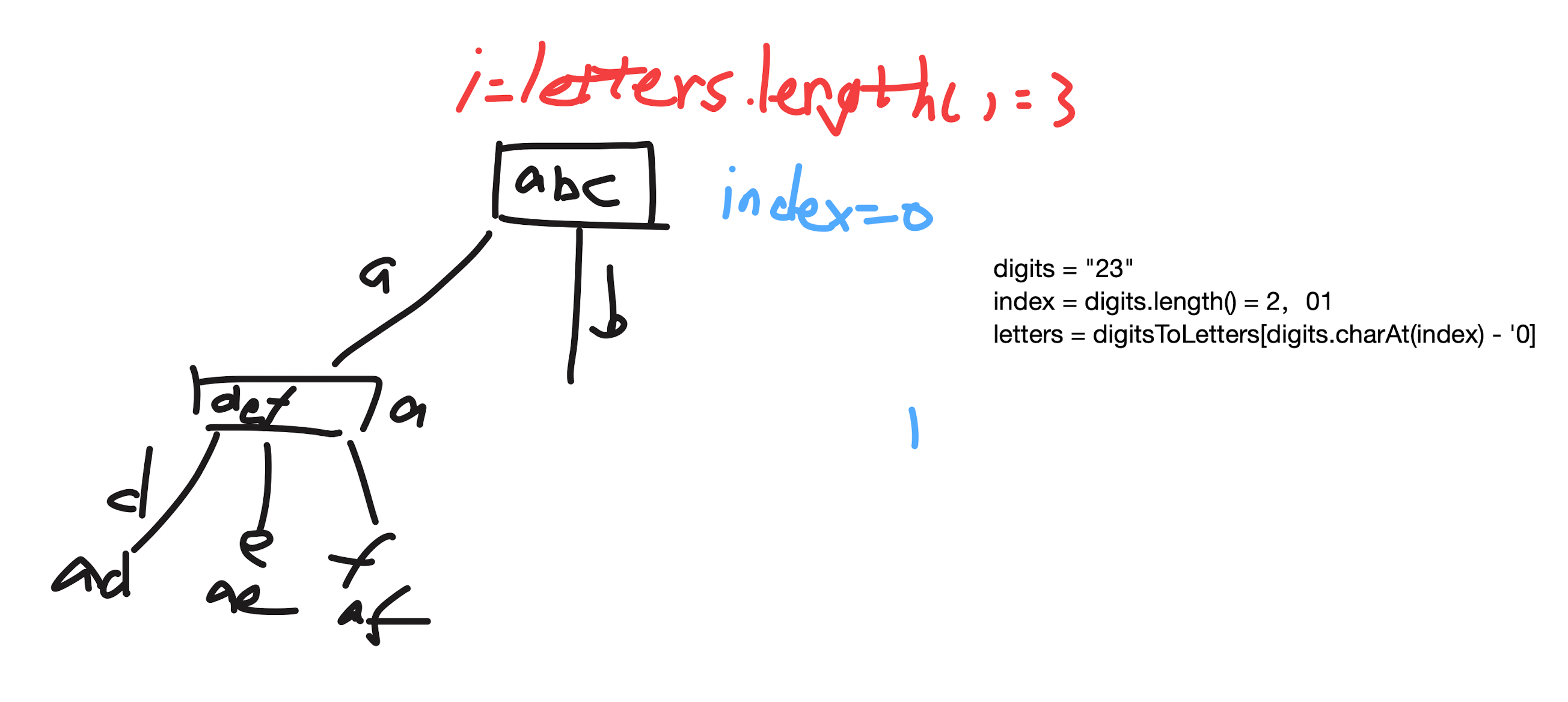
在这里插入图片描述

class Solution {
    String[] digitToLetters = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};

    StringBuilder path = new StringBuilder();
    List<String> result = new ArrayList<>();

    public List<String> letterCombinations(String digits) {
        backtrack(digits, 0);
        return result;
    }

    public void backtrack(String digits, int index) { // index：digits 的下标，即树的深度
        if (index == digits.length()) {
            result.add(path.toString());
            return;
        }

        int digit = digits.charAt(index) - '0'; 
        String letters = digitToLetters[digit];

        for (int i = 0; i < letters.length(); i++) { // letters.length()：树的宽度
            path.append(letters.charAt(i));
            backtrack(digits, index + 1);
            path.deleteCharAt(path.length() - 1);
        }
    }
}

评论区题解看到的迭代法，但只适用于每一层遍历都是从 0 开始的情况。还是回溯法更好更具有通用性。

public List<String> letterCombinations(String digits) {
        List<String> result = new ArrayList<>();
        int n = digits.length();
        if (n == 0){
            return result;
        }
        Map<Character, List<String>> map = new HashMap<>();
        map.put('2', Arrays.asList("a","b","c"));
        map.put('3', Arrays.asList("d","e","f"));
        map.put('4', Arrays.asList("g","h","i"));
        map.put('5', Arrays.asList("j","k","l"));
        map.put('6', Arrays.asList("m","n","o"));
        map.put('7', Arrays.asList("p","q","r","s"));
        map.put('8', Arrays.asList("t","u","v"));
        map.put('9', Arrays.asList("w","x","y","z"));
        result = map.get(digits.charAt(0));
        if (n == 1){
            return result;
        }
        int i = 1;
        while (i < n){
            List<String> temp = new ArrayList<>();
            for (String s1 : result) {
                for (String s2 : map.get(digits.charAt(i))) {
                    temp.add(s1+s2);
                }
            }
            result = temp;
            i++;
        }
        return result;
    }

回溯法总结

包含 5 类问题

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 棋盘问题：N皇后，解数独等等

模板：

void backtracking(参数) {
	if (终止条件) {
		收集结果;
		return ;
	}
	for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
		处理节点;
		递归函数;
		回溯操作;
	}
	return ;
}

回溯算法解决的任何问题都可以抽象成一棵树。
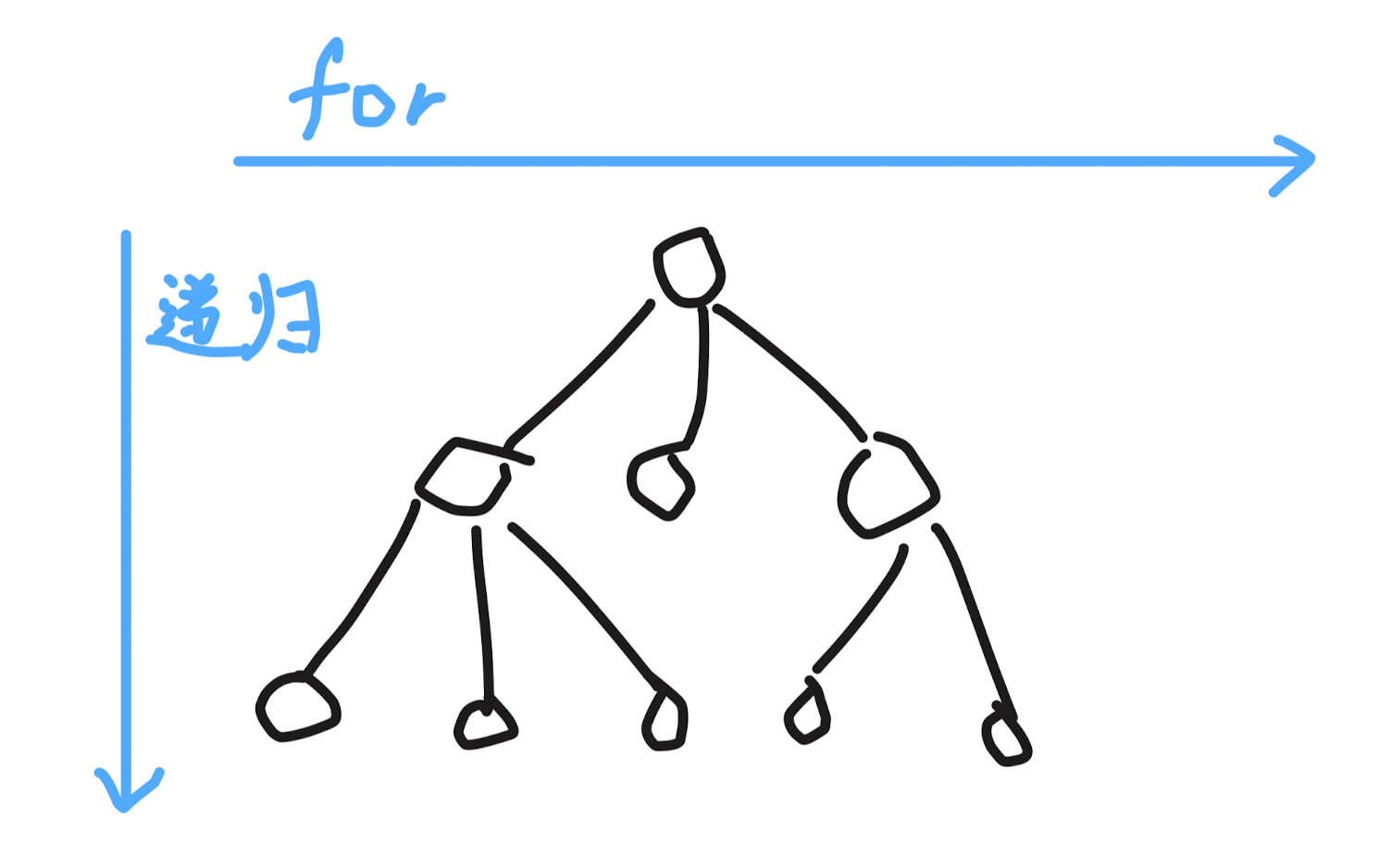
在这里插入图片描述

注：
组合、切割、排列和部分棋盘问题都是在叶子节点收集结果。
只有子集问题是在每个节点收集结果。

我对回溯法的理解：回溯法就是解决 Java 中没有办法可控 1~n 个 for 循环嵌套的问题，不然直接 n 个 for 循环暴力解决了。

代码随想录算法训练营Day25 | 216.组合总和III、17.电话号码的字母组合 | Python | 个人记录向
Python基本算法
04-27 1015
回溯算法：216.组合总和III、17.电话号码的字母组合。
代码随想录算法训练营第三天| 203.移除链表元素 707.设计链表| 206.反转链表
kkksij的博客
10-28 1185
建议： 本题最关键是要理解 虚拟头结点的使用技巧，这个对链表题目很重要。思路：1.直接使用原来的链表进行删除操作。 2.设置一个虚拟头结点在进行删除操作题目链接：. - 力扣（LeetCode）视频链接：手把手带你学会操作链表 | LeetC de：203.移除链表元素_哔哩哔哩_bilibili文章链接：手把手带你学会操作链表 | LeetCode：203.移除链表元素_哔哩哔哩_bilibili具体实现：定义一个cur = head 的结点，遍历链表，每次遍历时 cur.val 和
代码随想录算法训练营第22天 | 77. 组合、216.组合总和III、17.电话号码的字母组合
Athenaand的博客
08-01 904
第22天，继续加油。
代码随想录算法训练营第19天| 77. 组合，216.组合总和III，17.电话号码的字母组合
weixin_65605615的博客
08-06 315
思路：先把每个数字对应的字母写好，构成完整的可选列表。后面就是根据这个每一层遍历即可（和之前遍历1~9自然数一样）。
创作代码随想录算法训练营第22天 | 77. 组合 、216.组合总和III、17.电话号码的字母组合
2303_79169027的博客
08-02 1020
回溯算法第一次接触，感觉在形式上是递归加上循环，其中每一层的递归对应一套循环。这道组合的题目，开始接触解决方法是无脑的暴力搜索，但是组合的个数一多就不行了。为了解决这个问题，采用了回溯法，。首先回溯法也是结合了递归，首先要确定结束的条件，为当前结果数组中的个数是否等于要求的个数。接下来就是循环的判断，在每一层的循环中，首先将当前层的开始数字放进数组中，然后进入递归，递归出来后还需要当前层之前的数字弹出，达到回溯的效果。
代码随想录算法训练营第22天| 77. 组合、216.组合总和III 、17.电话号码的字母组合
2301_76253115的博客
11-21 352
最后一题有点小变化，可以再理解一下。理解一下相当于多层的循环遍历。学习链接：​​​​​​​。妈呀 完全自己写出来了。总体这三题思路差不多。
代码随想录算法训练营第22天| 77. 组合、216.组合总和III、 17.电话号码的字母组合
weixin_74933841的博客
12-04 290
回溯需要勤加练习。
代码随想录算法训练营第22天| 77. 组合 ，216.组合总和III，17.电话号码的字母组合
qq_44932556的博客
07-24 527
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。返回 所有可能的有效组合的列表。该列表不能包含相同的组合两次，组合可以以任何顺序返回。给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。你可以按 任何顺序 返回答案。哈希表、字符串、回溯。
代码随想录算法训练营第22天|77.组合、216.组合总和III、17.电话号码的字母组合
meiqiuxiaohei的博客
07-14 373
遇到的困难：对于for循环的边界条件不是很理解，i < letter[digits[startindex] - '0'].size()的意思是对于每个数字，只循环它对应字符串的大小进行处理就可以，比如说3对应‘abc’，则for循环3次。思想：回溯本质上是把for循环一层一层的包装起来，把数组当作全局变量比较方便。一层一层访问并添加，满足条件之后将值push进答案数组，然后向上一层回溯（把这一层push的元素pop掉之后结束这一层的遍历即可）。17.电话号码的字母组合。216.组合总和III。
代码随想录算法训练营第19天|77. 组合、216. 组合总和 III、17. 电话号码的字母组合
cjkjj的博客
07-01 420
回溯三部曲1. 确定回溯函数的返回值和参数本题中返回结果为一个List，回溯函数肯定不能返回List，返回值为void即可参数为n和k2. 确定递归中止条件找到k个数字的集合就中止本次回溯3. 确定单层递归操作每层递归函数内，从当前位置向后遍历数字，将数字加入过程集合，进入下一层，之后回溯。
代码随想录算法训练营第22天|77.组合、216.组合总和Ⅲ、17.电话号码的字母组合
qq_62407923的博客
03-22 227
然后不停的遍历和回溯，将符合要求的结果存下，最后return即可。与组合基本类似，就是多了限制条件，且元素只有1-9，回溯的参数(startidx和sum)，startidx是用于下一次回溯搜索时，从下一个数搜索，sum可有可无，可以定义全局变量，终止条件两个，当path.size() == k && sum == n，添加该path，否则跳过，然后return;首先明确组合与排列的区别，组合不关心元素的顺序，而排列关心，如[1,2],[2,1]对于组合来说是同一个结果，而对于排列来说就是两个不同的结果。
代码随想录算法训练营第一天 - 704. 二分查找
05-08
代码随想录算法训练营第一天 - 704. 二分查找
代码随想录算法训练营第一天- 977.有序数组的平方 ， 209.长度最小的子数组，59.螺旋矩阵II
10-12
代码随想录算法训练营第一天- 977.有序数组的平方 ， 209.长度最小的子数组，59.螺旋矩阵II
LeetCode热题100--70. 爬楼梯--简单
2301_80071187的博客
12-20 189
这道题考察爬楼梯问题，每次可以爬1或2个台阶，求爬到n阶的不同方法数。采用动态规划解法，初始化dp数组，dp[0]=1，dp[1]=1。对于i≥2，dp[i]=dp[i-1]+dp[i-2]，即当前台阶的方法数等于前两个台阶方法数之和。最终返回dp[n]即为结果。该解法时间复杂度O(n)，空间复杂度O(n)。
智驾空间智能、物理智能、世界模型相关的最新论文和开源算法链接
Bonaventure的博客
12-16 1034
这些资源涵盖了2025年自动驾驶领域的前沿研究，从空间推理到物理建模和世界模拟，提供了丰富的开源工具和理论框架。建议用户通过链接深入探索论文和代码，以应用于实际项目或进一步研究。如果您需要更详细的解读或特定应用建议，请随时补充信息！
【算法笔记】AC自动机
u012559967的专栏
12-19 720
AC自动机: AC自动机是一种高效的多模式字符串匹配算法，它巧妙地将 Trie树的字典结构与 KMP算法的失配指针思想相结合，能同时在一段文本中查找多个模式串的所有出现位置，广泛应用于敏感词过滤、生物信息学序列分析等领域。在字符串匹配领域，我们会遇到两类问题：单模式匹配：给定一个文本字符串和一个模式字符串，判断模式字符串是否出现在文本字符串中。《【算法笔记】KMP算法》多模式匹配：给定一个文本字符串和多个模式字符串，判断所有模式字符串是否出现在文本字符串中。解决方案：AC自动机算法。
(leetcode) 力扣100 15轮转数组（环状替代）
qq_62235017的博客
12-18 985
我们利用这个过程，首先计算需要多少个从起点走回起点的圈数（count，为数组长度与步数的最大公约数，具体推推导后面会给），然后再遍历每一圈，通过创建一个临时变量（current,next，类似于指针的作用），来存储需要移动的变量将其移动到下一个位置，而下一个位置变为信的需移动变量，直到走完当前圈数。我们可以把数组想象一个圆圈，如果我们每次固定步数前进，肯定会在有限圈数回到出发点，这个过程中，有可能会遍历完数组所有数，有可能遍历有限数。这句话的意思是：在这个游戏中，你启动一次任务，只能覆盖到。
力扣刷题笔记-组合总和
最新发布
qq_42622072的博客
12-21 426
比如candidates = [2,3,6,7], target = 7的时候，第一次先选一个数2，把2加入到path中，这时还没有达到target的值，可以再选一个数，这时还是可以按顺序选[2,3,6,7]中的所有数，做循环尝试，可以就再选2试试，这时path中已经有[2，2]了，和还是没达到target，还可以继续加数，再加一个2试试，最后发现[2，2，2]后面再加数已经不行了，加任何数都走不通了，那么就会把最后加进去的那个 2 踢掉，回到 [2, 2] ，然后在这一层尝试别的选择。
Leetcode 79 最佳观光组合
im_AMBER的博客
12-17 578
每个元素只遍历一次只用了两个变量O(n)O(1)公式拆分是核心：将原得分公式拆分为，把双变量问题转化为单变量的遍历问题。贪心维护最优值：遍历j时，用best维护之前所有i < j中的最大值，这样每一步只需要 O (1) 计算，整体时间复杂度是 O (n)。遍历顺序：因为要求i < j，所以从j=1开始遍历，先计算当前j的得分，再更新best（避免 j 自己和自己配对）。
代码随想录算法训练营第五天
02-17
### 关于代码随想录算法训练营第五天学习内容 #### 动态规划入门 动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。在第五天的学习中，重点在于理解并掌握动态规划的核心概念及其应用。 #### 解决斐波那契数列问题 斐波那契数列是一个经典的例子来介绍动态规划的思想。对于给定的n值，计算第n项斐波那契数值可以采用自底向上的方法构建解决方案[^1]： ```python def fib(n): if n <= 0: return 0 elif n == 1: return 1 dp = [0] * (n + 1) dp[1] = 1 for i in range(2, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[n] ``` 此实现方式避免了重复计算相同的子问题，从而提高了效率。 #### 攀爬楼梯问题 另一个典型的应用场景是攀爬楼梯问题，假设每次可以选择走一步或两步，则到达第n阶的不同路径总数也可以利用动态规划解决: ```python def climbStairs(n): if n == 1 or n == 2: return n dp = [0] * (n + 1) dp[1], dp[2] = 1, 2 for i in range(3, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[-1] ``` 上述两个案例展示了如何运用动态规划技巧有效地解决问题，并且强调了状态转移方程的重要性以及边界条件处理。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值