java-给一个数组，实现奇数在前，偶数在后的排序三种解法

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

思路一：从前向后找，找到一个数如果是偶数，就把这个数取出放到数组尾部，这个会产生数据的移动。时间复杂度也比较高，为O（n^2）。效率太低。

思路二：申请两个大小相等的数组，然后将奇数放在第一个数组中，偶数放在第二个数组中，然后把偶数数组拷贝到奇数数组中后面去。时间复杂度为O（n），空间复杂度为O（n）。

思路三：先计算出奇数的个数count，然后用双指针来遍历，一个从头遍历到count，一个从数组尾部遍历到count。从前向后找到一个偶数的下标，从后向前找到一个奇数的下标，然后交换对应的值。直到遍历完整个数组。时间复杂度为O（n），空间复杂度为O（1）。

当然无论从时间复杂度还是空间复杂度来说第三种方法更高效，所以我们在此利用第三种方法来实现。

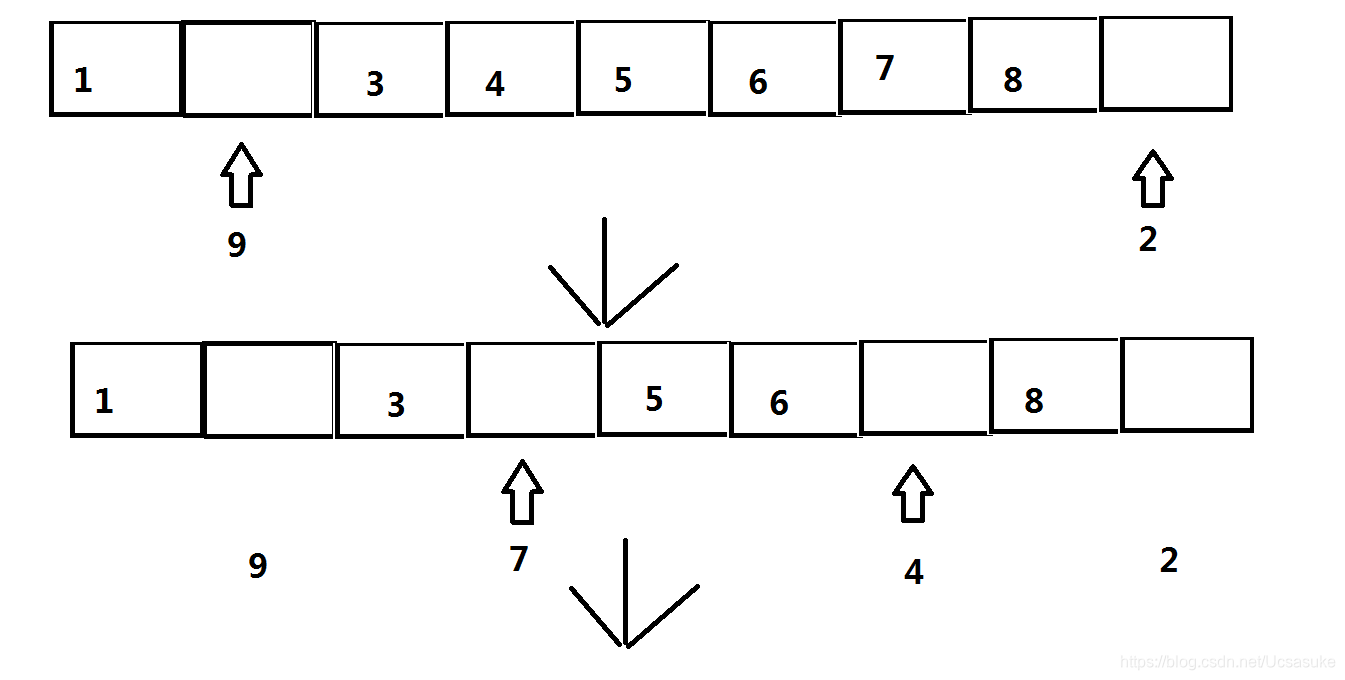
测试代码：

public static void main(String[] args) {
    int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
    fun(arr);
    System.out.println(Arrays.toString(arr));
}


private static void fun(int[] arr) {
    int front = 0,end = arr.length-1;//设置两个指针，一个指向头部，一个指向尾部
    if (arr.length == 0){//数组长度为0则返回
        return;
    }

    while (front < end){
        while (front < arr.length && arr[front]%2 == 1){//从前往后找偶数
            front++;
        }
        while (end >= 0 && arr[end]%2 == 0){//从后往前找奇数
            end--;
        }
        if (front < end){//将前面的偶数与后面奇数交换位置
            int temp = arr[front];
            arr[front] = arr[end];
            arr[end] = temp;
        }
    }
}

运行结果：