批标准化（Batch Normalization）

论文地址：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

BN是2015年提出的，现在已经被广泛地应用在神经网络当中。其实关于BN的方方面面在维基上有着很详细的阐述，想深入研究的同学可以看一看。

以下我只稍微讲讲我觉得比较重要的部分。

为什么要进行BN？

简单一句话，就是为了训练参数更好更有效地向前传播。

而为什么参数会出现不好传播的情况呢？主要原因是激活函数的使用。为了增加模型的非线性表达能力，在层与层之间常常加上一层激活函数。而这层激活函数的存在会使得数据分布产生变化，大部分激活函数都会有一个敏感区间，而非敏感区间的数据有可能就在多层的参数传递后丢失了。尤其是在层数特别深的情况下，未经过标准化的数据起到的作用相当有限。

这个情况有一个名词，叫内部协变量偏移（ internal covariate shift），即在训练过程中每一层网络的数据分布上参数的初始化与变化（层层叠加），将会影响整个网络的学习率。BN最初提出就是为了解决这个问题，但BN与covariate shift之间的关系实际上是未经实验严格证明的。

所以，BN层的作用是把一个mini-batch内的所有数据，从不规范的分布拉到正态分布。这样做的好处是使得数据能够分布在激活函数的梯度较大的区域，因此也提高了泛化能力，可以在一定程度上解决梯度消失的问题，同时可以减少dropout的使用。

当参数更好地向前传播后，梯度的下降会更加稳定，可以使用更大的学习率来加快学习。对数据分布的不断调整也减轻了对参数初始化的依赖，利于整体调参。

如何进行BN（BN的正向传播过程）？

BN其实就是将batch内的数据实现均值为0，方差为1的正态分布。BN一般放在激活函数之前。

如下图，步骤很简单：

1. 计算mini-batch中的均值（mini-batch mean）
2. 计算mini-batch内的方差（mini-batch variance）
3. 对每一个元素进行归一化（normalize）。我们知道正态分布的表达式是，其中是为了mini-batch的数值稳定性而加到方差中的一个常数。如果忽略它，每一个mini-batch的元素都是采样于同一个数据分布的值。
4. 进行尺度缩放与偏移操作（scale and shift）：其中偏移（对应于均值）和尺度（对应于方差）为参数，通过训练来学习的。目的是为了补偿网络的非线性表达能力。

为什么是mini-batch？

主要是由于目前主流的梯度更新方式是mini-batch gradient decent，小批的梯度下降，这种方法把数据分为若干个批，按批来更新参数，这样，一个批中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多，计算量也不是很大。

当mini-batch中只有一条数据，如何确定1.2.中的均值与方差？

可以采用训练收敛最后几批mini batch的 𝜇和𝜎的期望，作为预测阶段的𝜇和𝜎。

为什么？一开始我们就想用所有数据的均值和方差，但是对于模型训练迭代是不现实的，所以用了mini-batch的均值和方差。现在训练收敛最后几批的数据分布，可以看作是全局的数据分布，其均值和方差可以直接用当然更好。

BN的训练过程？

整个训练过程没有什么特别的，只是加上了BN层进行计算而已。但当训练结束后，每一层的BN就不是很必要了，因为它的两个参数和已经固定，inference时BN可以用一个线性变换来替换（11行）。

 BN的反向传播？

其实这就是用传播图与链式法则求导而来，原文中没有过多解释。我试了试，推的过程不是很难，就是要注意函数之间的复合情况，画一个计算图更不容易漏掉。

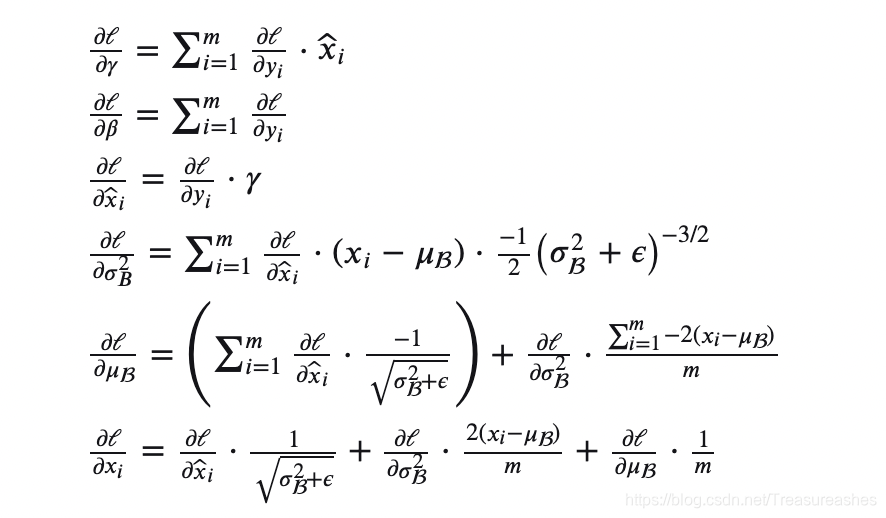
卷积层如何使用BN？

一个卷积核产生1个feature map， 一个feature map 就会有1对参数和。为了在卷积层上保持BN的性质，不仅要在mini-batch之间进行BN，也要在不同的位置的feature map之间进行BN。对于卷积层来说，不是在每个激活元之间共享参数，而是跨mini-batch的feature map 要共享一对参数。

所以此时，在算法中的从一个mini-batch（size m）的所有值集合变成了跨mini-batch的feature map（size m p q）的所有值集合。参数对的个数也从p*q*c（channel）变成了c。

如果还不是很理解，可以看这个答案：Batch Normalization in Convolutional Neural Network