[nlp] MLE，EM，MAP 三种算法对比和理解

参考：https://blog.youkuaiyun.com/zjm750617105/article/details/52696006

MLE（最大似然估计），EM（期望最大值估计），MAP （最大后验概率）

一、MLE
MLE是在“模型已定，参数未知”的情况下根据给定观察序列（所有序列服从同一分布）估计模型参数的估计方法。模型参数的准确性，跟观察序列直接相关。
最大似然估计(MLE)的计算过程是:
　　（1） 写出似然函数（已知模型，即已知概率密度函数）
　　（2） 对似然函数取对数，并整理
　　（3） 求导数
　　（4） 解似然方程

二、EM
EM 算法就是含有隐变量的MEL。 下例中的隐变量就是课程（数学 和 英语）。

抽取的成绩时，我们不知道哪些成绩是数学成绩，哪些成绩是英语成绩，，而数学和英语的成绩都满足正态分布，这时候应该怎么求这些参数呢 ？

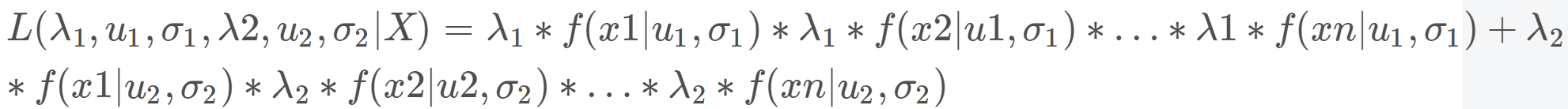
这就出现了隐变量的引入，就是我直接求L（θθ |X）不好求。我必须先知道成绩是英语还是数学然后再求参数，即：
L（θ|X）=p（x|z,θ）p（z|θ