【汽车功能安全】ECC校验原理

快乐工作，快乐生活！

通讯作者lixingyi09@qq.com 

---

目录

0. Glossary

1. 奇偶检验

2. ECC

2.1 Data Transmission with ECC Code

2.2 SEC

2.3 代码的实现

2.4 SECDED

总结

参考文献：

---

通信作者：940900746@qq.com

---

0. Glossary

ECC - Error Correction Code

SEC - Single Error Correction 

DED - Double Error Detection 

SECDED - Single Error Correction Double Error Detection 

Correctable Error - Single bit Error

Un-Correctable Error - Multiple bits error

1. 奇偶检验

奇偶校验（parity）增加一个校验位来检查数据是否正确。当数据中1的位数为奇数个时，校验位为1；否则校验位为0。

也就是说在数据和校验位总共的1的位数为偶数个时，数据被认为是正确的；否则数据被认为是奇偶校验错误。

如果你觉得我说的很绕，没有关系，看下面的这个表格。这下能看明白了吧。

Ø奇校验：确保整个被传输的数据中“1”的个数是奇数个，即载荷数据中“1”的个数是奇数个时校验位填“0”，否则填“1”；

Ø偶校验：确保整个被传输的数据中“1”的个数是偶数个，即载荷数据中“1”的个数是奇数个时校验位填“1”，否则填“0”。

 图1.1 奇偶校验

奇偶校验有两个不足的地方：

• 当出错的位数为偶数个时，奇偶校验会认为没有出错
• 奇偶校验只能反应数据出错，无法知道出错的到底是哪一位，无法恢复数据

奇偶校验常用于低速外设计接口，如UART。

重点来了!

图1.2 richard hamming 

理查德·汉明（Richard Hamming）发明了汉明纠错码（ECC），可以检查错误的同时做到纠错，因此获得了1968年的图灵奖。汉明码可以做到一位纠错两位检错。

什么是一位纠错两位检错呢？接下来会娓娓道来。

---

---

---

2. ECC

2.1 Data Transmission with ECC Code

图2.1 Data Transmission with ECC Code

(1) On Tx side, “ Pm_Ori ” is ECC generated and attached to the raw data

(2) Data is transmitted from Tx to Rx

(3) On Rx side, the received data is put into “ECC Gen” with the same algorithm, then calculate “ Pm_Gen ”

(4) Syndrome = Pm_Ori ^ Pm_Gen

If Syndrome == 0, there is no error bit, data transmission is correct

Otherwise, one-bit flip error occurs during transmission

2.2 SEC

计算汉明纠错码的步骤如下[1]：

1. 从左向右从1开始依次编号
2. 编号为2的幂次的位为奇偶校验位（1，2，4，8，16，……）对应图中绿色的Parity1和Parity2和Parity4,...

图2.2 parity的个数

1. 剩余其他位用作数据位（编号3，4，5，6，7，9，10，11，12，13，14，15，……）
2. 奇偶校验位的位置决定了与之相关的数据位，具体见下图1所示
3. 设置奇偶校验位，为各组进行偶校验

 

图2.3 绘制汉明码纠错表格 

With m parity bits, ECC can protect raw data width (2^m) – m – 1

Why minus “1”?

It corelates to “No Error” scenario

See the example above

•  m=5 (P0~P4), it can protect (2^5) – 5 – 1 = 26
• In (power of 2) Byte transfer, 26 bits can cover up to 2B, i.e. 16bit

校验位检查的数据位说明如下：

首先解释：对应图中的‘X’，这也就是‘X’是怎么来的？

校验位1（p1）检查1（01），3（11），5（101），7（111），9（1001），11（1011），……位，它们的编号2进制最右边第一位是1

校验位2（p2）检查2（10），3（11），6（110），7（111），10（1010），11（1011），……位，它们的编号2进制最右边第二位是1

校验位4（p4）检查4（0100），5（0101），6（110），7（111），12~15，20~23，……位，它们的编号2进制最右边第三位是1

校验位8（p8）检查8~15，24~31，40~47，……位，它们的编号2进制最右边第四位是1

注意，这里每一个数据位至少被2个校验码覆盖。

按照上面的步骤得到了汉明纠错码之后，就可以根据奇偶校验位来确定是哪一位数据出错了。在上图中的12位编码中，如果奇偶校验结果（p8,p4,p2,p1）的值为0000，则说明数据没有错。

假设数据某一个bit位发生翻转，如果四个校验位值为4'b1010，即'd10，那么就是下图第10位也就是这里的d5出错了。此时可以通过反转d5进行纠错。

图2.4 错误的bit位

举个例子：'h9A，就是2进制的1001_1010，按前述步骤编码的结果见如下图。

 

图2.5 汉明码表格

编码后的结果位0  1  1  1_0 0 1 0_1010。

                        p1 p2   p4          p8

(需要说明的地方是p1 p2 p4 p8 红色标记 的值不是随机给的，是要保证这些值填入到上图表格中1的个数为偶数。)

如果第9位（d4）出错变为011100100010。此时我们来做下奇偶校验。

图2.6 假定d4出错

p1的校验结果：011100100010有3个1，为奇性；该组有错误。

p2的校验结果：011100100010有4个1，为偶性；该组没有错误。

p4的校验结果：011100100010有2个1，为偶性；该组没有错误。

p8的校验结果：011100100010有1个1，为奇性；该组有错误。

综合校验结果，数据的第(1+8=)9位出错了，翻转一下第9位即可实现纠错。也就是d4。如果是奇偶校验无法发现问题。

图2.7 error bit

同样的，

{P8,P4,P2,P1} = 'b1001

 从列的角度看，只有位编号等于9的那一列是1001，也就是说d4数据位出错！

2.3 代码的实现

举个例子：

原始数据:10101. 5bit数据（D0，D1，D2，D3，D4），需要4bit校验位

P1 = D0 ^ D1 ^ D3 ^ D4

P2 = D0 ^ D2 ^ D3

P3 = D1 ^ D2 ^ D3

P4 = D4

原始数据：1001_1101, 8bit 数据，也需要4bit校验(参考下图4)

P1 = D0 ^ D1 ^ D3 ^ D4 ^ D6

P2 = D0 ^ D2 ^ D3 ^ D5 ^ D6

P3 = D1 ^ D2 ^ D3 ^ D7

P4 = D4 ^ D5 ^ D6 ^ D7

图2.8 对应8bit数据汉明码

 5bit数据实现的代码如下：

Table-1 

ecc[0] = dataecc[0] ^ dataecc[1] ^ dataecc[3] ^ dataecc[4];
ecc[1] = dataecc[0] ^ dataecc[2] ^ dataecc[3];
ecc[2] = dataecc[1] ^ dataecc[2] ^ dataecc[3];
ecc[3] = dataecc[4];

本文重点知识讲解：

 图2.9 32bit数据汉明码表格

P1         = D[0] ^ D[1] ^ D[3] ^ D[4] ^ D[6] ^D[8] ^ D[10] ^ D[11] ^ D[13] ^ D[15] ^ D[17] ^ D[19] ^ D[21] ^ D[23] ^ D[25] ^ D[26] ^ D[28] ^ D[30]
P2         = D[0] ^ D[2] ^ D[3] ^ D[5] ^ D[6] ^ D[9] ^ D[10] ^ D[12] ^ D[13] ^ D[16] ^ D[17] ^ D[20] ^ D[21] ^ D[24]  ^ D[25] ^ D[27] ^ D[28] ^ D[31]
P4         = D[1] ^ D[2] ^ D[3] ^ D[7] ^ D[8] ^ D[9] ^ D[10] ^ D[14] ^ D[15] ^ D[16] ^ D[17] ^ D[22] ^ D[23] ^ D[24] ^ D[25] ^ D[29] ^ D[30] ^ D[31]
P8         = D[4] ^ D[5] ^ D[6] ^ D[7] ^ D[8] ^ D[9] ^ D[10] ^ D[18] ^ D[19] ^ D[20] ^ D[21] ^ D[22] ^ D[23] ^ D[24] ^ D[25]
P16       = D[11] ^ D[12] ^ D[13] ^ D[14] ^ D[15] ^ D[16] ^ D[17] ^ D[18] ^ D[19] ^ D[20] ^ D[21] ^ D[22] ^ D[23] ^ D[24] ^ D[25]
P32       = D[26] ^ D[27] ^ D[28] ^ D[29] ^ D[31]

这里就不一一展开啦，但是可以看到的是。32bit数据，需要的校验位是6bit。

同样SEC的缺点也是很明显，如果有2bit位的数据发生错误，比如说数据位和奇偶校验位出错，

图2.10 2bits flipped

 这样即使纠错的结果也是不正确的，这时候就需要检测2bit错误信息。

2.4 SECDED

在纠错编码的基础上再增加一位给所有数据的奇偶校验，这样就可以纠错1位并且检测2位错。(如下图P72)

纠错码奇偶校验位（H）和最后追加的全组奇偶校验（h）可能存在以下四种情况：

• H为偶h为偶，数据没有错误 (正常的情况下，偶数个校验位，额外的校验位肯定是0)
• H为奇h为奇，数据有1位可纠正的错误（校验位为奇数，额外校验位必须是1）
• H位偶h为奇，仅有h位出错，h位取反即可（H为0，h理所应当是0，如果是1，取反）
• H为奇h为偶，发生了2位错（说明2bit错误）

纠1位错、检2位错（SEC/DED）这种技术在内存中广泛使用。特别是对于8字节字块做SEC/DED刚好需要一个字节的额外开销。

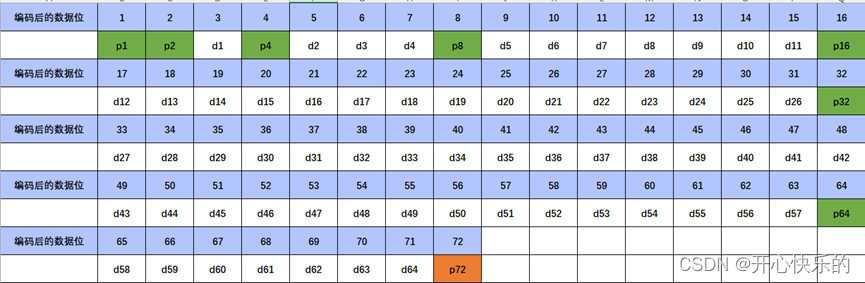
图2.11 SEC/DED 

 上图中，p1/p2/p4/p8/p16/p32/p64是用来一位纠错的奇偶校验位，p72是整组数据的奇偶校验位。奇偶校验位总共8位一个字节。

如果上述的内容不好理解的话，也可以这样理解：

图2.12 2bit检错 

Extra parity bit – Pe

• Regarding to Bit Index, with even number of “x” in the table, those bits will be involved into Pe calculation
• Pe = D0^D1^D2^D4^D5^D7^D10^D11^D12^D14

In the same case above

{Pe,P4,P3,P2,P1,P0} = 6’b10_0010 = ‘d34 > 21, means two bits error is detected

这些内容与上述的描述有着异曲同工之妙。每个读者的理解不同，所以看到问题的角度不同。

总结

ECC 1bit纠错理解比较容易，2bit可能会复杂一些，本文没有详细的说明。有任何的疑问，可以和我讨论！

参考文献：

[1]奇偶验码、ECC纠错检错算法 - 知乎 (zhihu.com)

 [2]ECC校验——汉明码（Hamming Code）_错误检测(ecc) :1个字节。采用hamming code的方式_北北纬30°的博客-优快云博客