非线系统控制算法学习3_双控制器设计(线性系统控制理论回顾)

非线系统控制算法学习3_双控制器设计(线性系统控制理论回顾)

1 引言

  在第一篇文章中，探讨了反馈线性化的理论，让系统可以收敛到平衡点。但在实际仿真测试中发现系统的超调量和调节时间等参数还是不够理想。在本文中，将使用反馈线性化和全状态反馈两个控制器共同完成对单摆系统的控制工作。并使用线性二次型调节器寻找控制器最佳参数。最后通过Simulink仿真来验证设计是否有效。

2 控制器设计

2.1 双控制器设计基本方案

  在第一篇文章中，使用反馈线性化方法消除系统的非线性部分，并使用Laypunov函数限制所构建的控制器中的参数，使得系统是渐进稳定的。这就意味着，系统控制的性能很大程度上取决于Laypunov函数的选择，不同的Laypunov函数往往会给出不完全相同的参数限制条件。而Laypunov函数的选择往往不存在统一的方法，且用Laypunov函数判断系统稳定性是一个充分条件，这就给直接使用反馈线性化控制器让系统达到理想的控制性能是困难。在此基础上，提出一种双控制器设计方案：使用反馈线性化使得系统稳定和线性化，利用全状态反馈控在系统已经线性化和稳定的基础上，调节系统的控制性能。两种控制器相互配合，以达到良好的控制效果。

图1-双控制器控制流程图

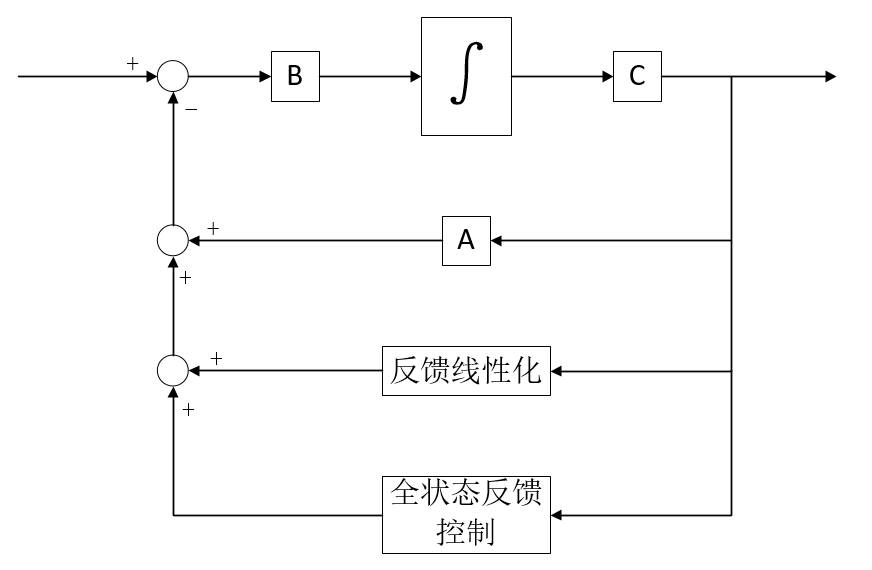
  反馈线性化部分已经在第一篇文章中进行了详细的讲解，在本文将重点阐述全状态反馈控制器的设计方法。

2.2 受控单摆系统的能控性与能观性

2.2.1 能控性能观性定义

  在进行正式的全状态反馈控制器设计器设计以前，首先需要评估系统的能控性和能观性。只有当系统是能控的，设计控制器才是有效的。如果系统是能观的，才可以考虑使用输出反馈来代替状态反馈。
  对于一个标准的$n$阶LTI系统，其状态方程和输出方程可以表示为：
$$\begin{gathered} \dot{\mathbf{x}}(t)=\mathbf{A}\mathbf{x}(t)+\mathbf{B}\mathbf{u}(t) \\ \mathbf{y}(t)=\mathbf{C}\mathbf{x}(t)+\mathbf{D}\mathbf{u}(t)\text{\hspace{1em}(2-1)} \end{gathered}$$
  能控性定义：
  如果存在无约束的控制信号$u(t)$能够让系统从任意一个初始状态$x(t_0)$变化到任意一个指定的预期状态$x(t)(t_0\le t\le T)$，则称系统是完全能控的。
  定义能控性矩阵：
$$\mathbf{S}=\left[\begin{array}{ccccc}B& AB& A^{2}B& \cdots & A^{n-1}B\end{array}\right]\text{\hspace{1em}(2-2)}$$
  系统完全能控的充分必要条件为，能控性矩阵的秩为系统的阶数：
$$rank(S)=n\text{\hspace{1em}(2-3)}$$

  能观性定义：
  在给定控制变量$u(t)$后，可以由输出$y(t)$在有限时间段$T$内的观测值确定系统的初始状态，则称系统是完全能观的。
  定义能观性矩阵：
$$\mathbf{Q}=\left[\begin{array}{c}C\\ CA\\ C{A}^2\\ ⋮\\ C{A}^{n-1}\end{array}\right]\text{\hspace{1em}(2-4)}$$
  系统完全能控的充分必要条件为，能控性矩阵的秩为系统的阶数：
$$rank(Q)=n\text{\hspace{1em}(2-5)}$$

2.2.2 受控单摆系统的能控能观分析

  为配合系统能控性和能观性分析，将反馈线性化之后的系统改写为：
$$\begin{gathered} \left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -K& -b\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ c\end{array}\right]u \\ y=\left[\begin{array}{cc}0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\text{\hspace{1em}(2-6)} \end{gathered}$$
  其中：$K=1;b=0.5;c=5$。
  计算系统（2-6）的能控性和能观性
  能控性计算：
$$\begin{gathered} \mathbf{S}=\left[\begin{array}{cc}B& AB\end{array}\right]=\left[\begin{array}{cc}0& c\\ c& -bc\end{array}\right] \\ rank(\mathbf{S})=2\text{\hspace{1em}(2-7)} \end{gathered}$$
  能观性计算：
$$\begin{gathered} \mathbf{Q}=\left[\begin{array}{c}C\\ CA\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -K& -b\end{array}\right] \\ rank(\mathbf{Q})=2\text{\hspace{1em}(2-8)} \end{gathered}$$
  综上所述：受控单摆系统是能控能观的。

2.3 全状态反馈控制器设计

2.3.1 状态反馈的思想

  在控制领域，有状态反馈和输出反馈两种反馈方式。而对于所有LTI系统的控制，归根结底就是寻找到一种方法，使得系统的极点可以被配置到复平面的任意位置。在实际控制器的设计中，因为输出变量的获取往往比状态变量的获取更为方便直接，所以输出反馈更容易实现。但根据上面2.2.1小结关于能观性的定义，不难发现，并非所有的系统的输出变量都可以表征系统的全部信息。为了让系统能够获得更加全面的反馈信息，使用状态反馈，特别是全状态反馈就显得很有必要。一般的，全状态反馈可以表示为：
$$\mathbf{u}(t)=f[\mathbf{x}(t)]\text{\hspace{1em}(2-9)}$$
  可以很自然地想到，如果$f[\mathbf{x}(t)]$是一个简单线性函数，就可以实现极点的任意配置，那整个控制器的结构就会被大大简化。这样的思想已经被前人所证实，也逐渐成为全状态反馈设计的核心思想。及使用状态的增益作为系统的反馈量，实现对系统极点的任意配置。

2.3. 全状态反馈控制器设计流程

  令状态反馈的信号为：
$$\mathbf{u}(t)=-\mathbf{k}\mathbf{x}(t)\text{\hspace{1em}(2-10)}$$
  可以得到闭环系统的状态方程为：
$$\begin{gathered} \dot{\mathbf{x}}(t)=\mathbf{A}\mathbf{x}(t)+\mathbf{B}\mathbf{u}(t)=\mathbf{A}\mathbf{x}(t)-\mathbf{B}\mathbf{k}\mathbf{x}(t) \\ =(\mathbf{A}-\mathbf{B}\mathbf{k})\mathbf{x}(t)\text{\hspace{1em}(2-11)} \end{gathered}$$
  则闭环系统的特征方程为：
$$det(\lambda \mathbf{I}-(\mathbf{A}-\mathbf{B}\mathbf{k}))=0\text{\hspace{1em}(2-12)}$$
  如果系统是可控的，则说明可以通过改变状态反馈的比例系数$\mathbf{k}$，将系统的极点配置到复平面内的任意位置，从而完成对系统控制性能的调节。
  对本系列的研究对象受控单摆来说：
  假设， 希望系统的特征值${\lambda }_{1,2}=-10$，则系统的预期的特征多项式为：
$${\lambda }^2+20\lambda +100=0\text{\hspace{1em}(2-13)}$$
  对比式（2-12）和（2-13）的系数，可以得到反馈系数：
$$\mathbf{k}=\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right]=\left[\begin{array}{c}19.8\\ 3.9\end{array}\right]\text{\hspace{1em}(2-14)}$$

3 线性二次型调节器优化

  在前面的章节，均是在预期特征值已知的情况下完成的，如何选择特征值同样是控制器设计过程中需要考虑的问题。一般的如果希望收敛速度快，则系统的输入值就会增加，从而造成系统能耗的增加，也就是说系统的收敛速度和能耗之间是一对矛盾量。为了平衡这对矛盾量，需要引入最优控制的思想。所谓最优控制，就是给一个系统的综合指标（代价函数），通过设置不同的校正方法，使得系统综合指标达到最小值，这个过程称为最优控制。在本小节讨论的是一种简单的线性二次型控制。
  定义一个常见的代价函数：
$$\begin{gathered} J={\int }_0^{\infty }{\mathbf{x}}^T\mathbf{Q}\mathbf{x}+{\mathbf{u}}^T\mathbf{R}\mathbf{u}dt \\ \mathbf{Q}={\mathbf{Q}}^T\mathbf{R}={\mathbf{R}}^T\mathbf{Q}\ge 0\mathbf{R}\ge 0\text{\hspace{1em}(3-1)} \end{gathered}$$

${\mathbf{x}}^T\mathbf{Q}\mathbf{x}$ ——实际状态与期望状态（平衡点）之间的距离，权重为$Q$。
${\mathbf{u}}^T\mathbf{R}\mathbf{u}$ ——输入量的大小，权重为$R$。

  可以发现，这种代价函数的被积函数是一个二次型的形式，所以这种控制方式也叫线性二次型控制。如果设置矩阵$\mathbf{Q},\mathbf{R}$为对角矩阵，且对角线上每个元素都大于等于0，那被积函数就是一个标准二次型的形式。及只考虑每个状态变量自己对代价函数的影响，而不考虑状态变量耦合对代价函数的影响。
  因此在本文中目标变为：通过改变反馈系数$\mathbf{k}=\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right]$，寻找到代价函数式（3-1）的最小值。
  关于寻找代价函数$J$取最小值时对应的反馈系数${\mathbf{k}}_{\mathbf{LQR}}$，需要求解Riccati方程。方程的具体求解过程可以交给Matlab进行处理。具体代码如下：

clc
%设置系统矩阵和权重矩阵
%具体权重可根据任务需要进行设置
A = [0 1;-1 -0.5];
B = [0;5];
Q = [50 0 ;0 1];
R = 20;
%计算反馈系数
k = lqr(A,B,Q,R)

  本文设置权重的依据是，希望收敛速度尽可能快的同时，输入量尽可能的小。计算结果为：
$${\mathbf{k}}_{\mathbf{LQR}}=\left[\begin{array}{c}{k}_{LQR1}\\ k_{LQR2}\end{array}\right]=\left[\begin{array}{c}1.3937\\ 0.6858\end{array}\right]$$

4 仿真测试

  双控制器下受控单摆Simulink仿真模型如下图所示：

图2-双控制器下受控单摆Simulink仿真模型图

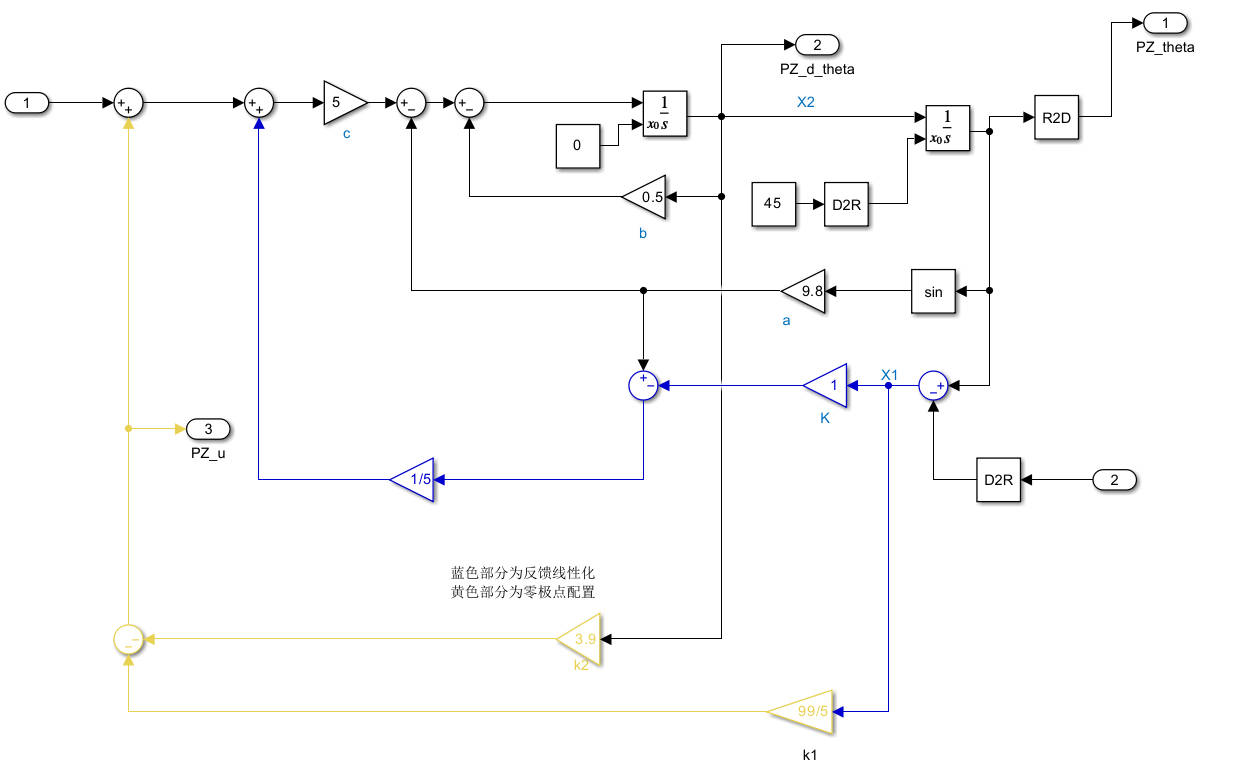
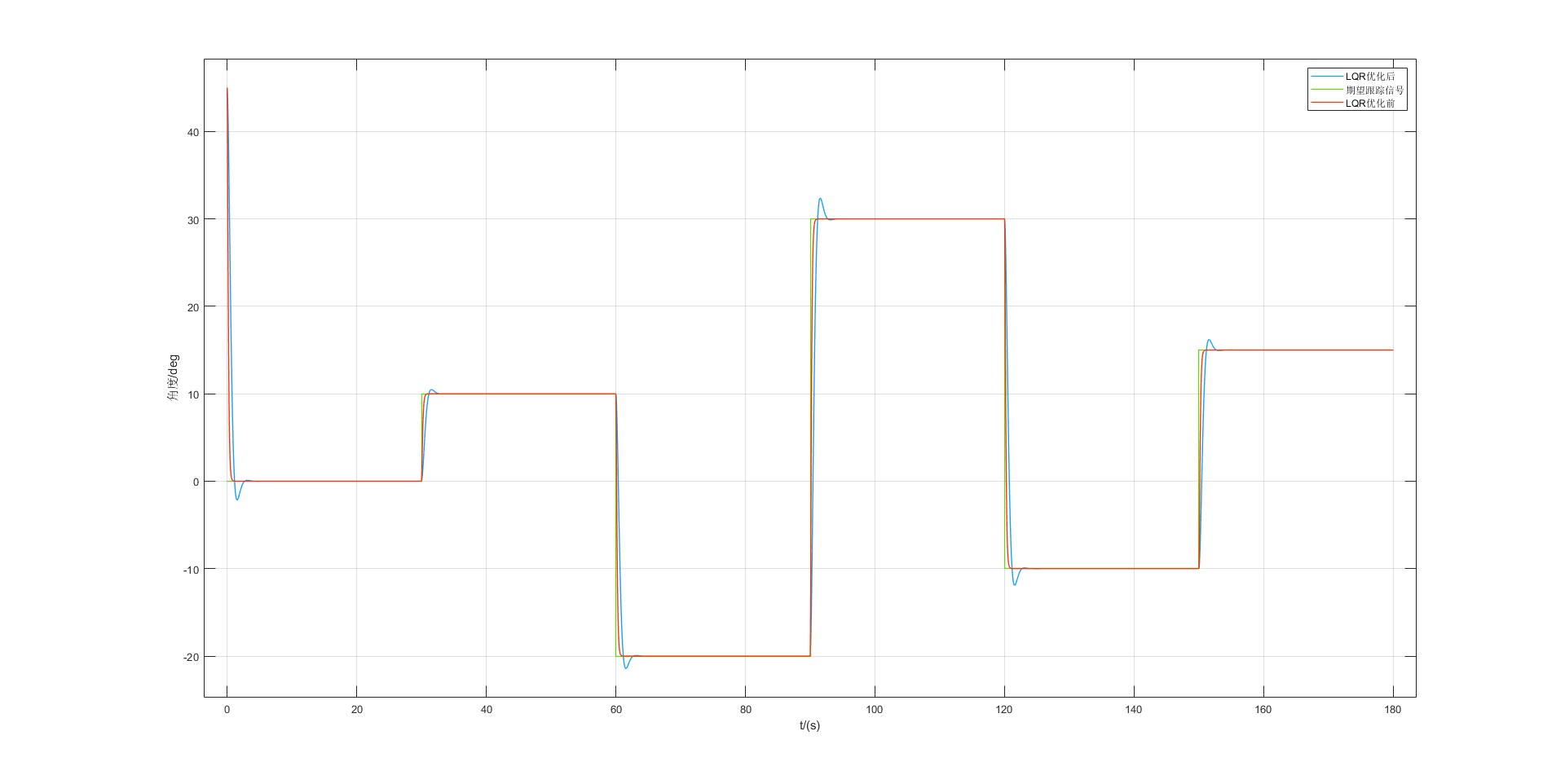
  对比直接使用零极点配置和使用线性二次型调节器优化参数的结果如下：
  动态响应：

图3-不同参数设置下响应曲线图

  输入量：

图4-不同参数下的输入量图

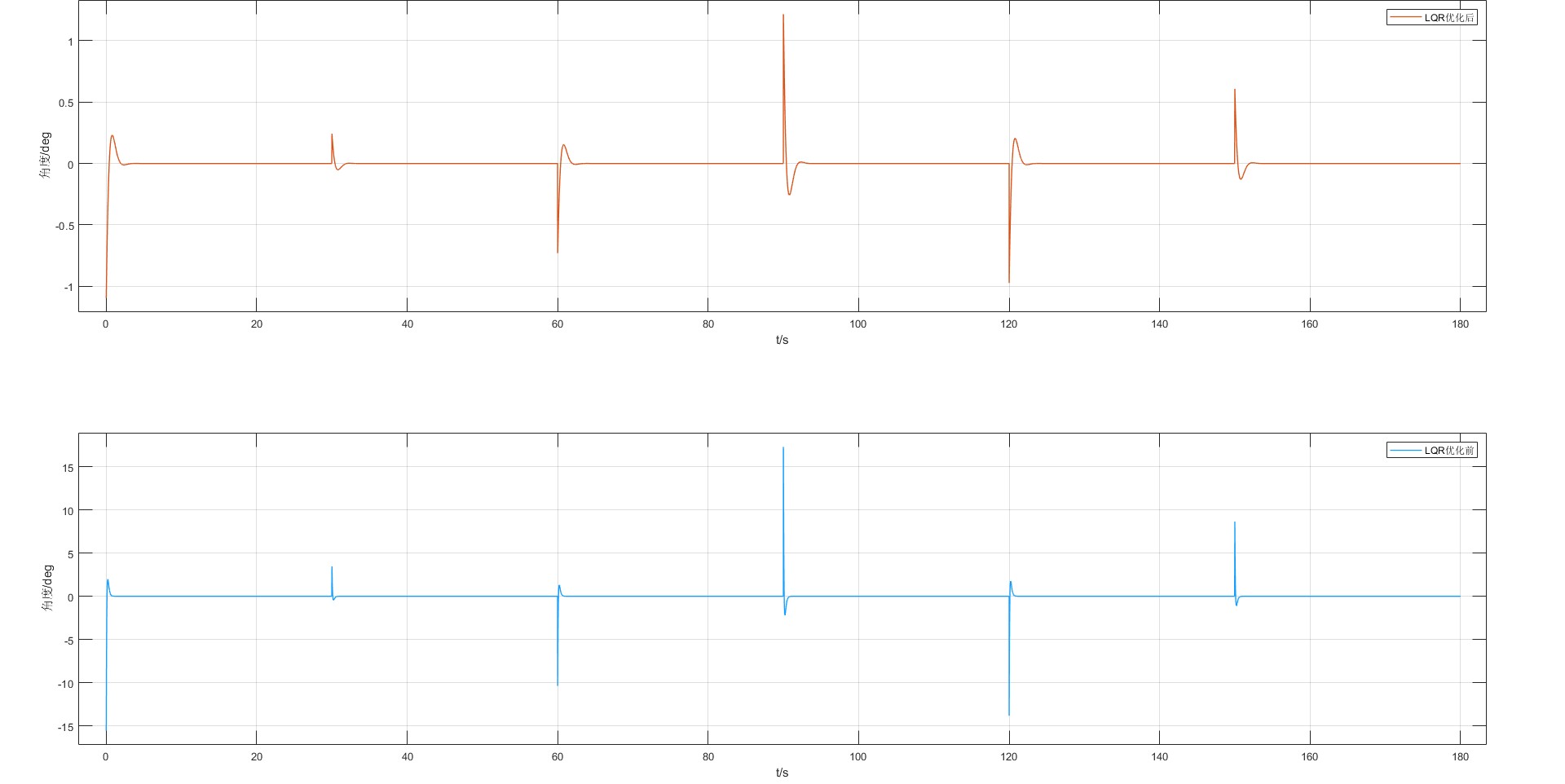
  通过对比图2和图3可以发现，使用LQR对全状态反馈控制器优化以后，虽然牺牲了一部分动态响应性能，但换脸的是输入量的大幅度降低。这在实际的控制器设计中，将有效的降低对实际控制器输入性能的要求，从而降低成本。

5 总结

  本文回顾了经典的线性系统控制理论，并提出了一种双控制器设计方案。通过反馈线性化消除系统的非线性部分，并利用Laypunov函数使系统渐进稳定。然后，利用全维观测器调节系统的控制性能。根据受控单摆系统的能控性和能观性，设计了全状态反馈控制器，并通过改变状态反馈的比例系数k，将系统的极点配置到复平面内的任意位置成为可能，从而实现了对系统控制性能的调节。此外，本文还讨论了线性二次型调节器（LQR）优化，通过定义代价函数，平衡系统的收敛速度和能耗，最终通过求解Riccati方程，找到代价函数最小值时对应的反馈系数​。仿真测试结果表明，使用LQR优化后的全状态反馈控制器虽然牺牲了一部分动态响应性能，但显著降低了输入量，从而降低了实际控制器的成本。综上所述，本文提出的双控制器设计方案，通过反馈线性化和全状态反馈控制器的结合，显著提高了系统的控制性能，并通过LQR优化进一步降低了系统的能耗。