Support Vector Machine理论推导证明（一）

春招华为面试竟然让手推SVM，当时真的不会，学的时候只是理解了一下,吃了大亏，于是决定每周推一次，温故而知新嘛。

支持向量机的动机来源于对线性感知机模型的修正。又称为最大化间隔（maximize margin）。分为硬间隔和软间隔。今天先总结手推一下。

SVM的关键就是无约束优化条件的转换、KKT条件以及核方法。

SVM包含soft margin和hard margin，这一点与Perceptron algorithm类似

函数间隔：

                                                                              

                                                                                     

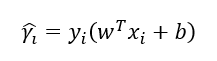
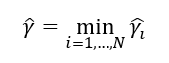
几何间隔：

                                                                              

                                                                                         

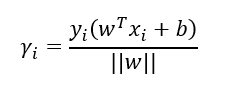
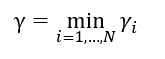
最大化间隔的数学表示：

                                                                

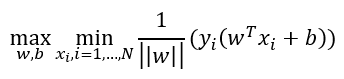
也就是各个样本点到分割超平面的最小间隔最大化，换一种更具体的写法：

                                                              

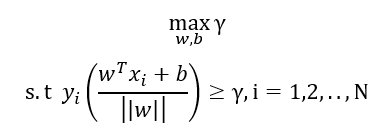
将几何距离用函数距离代替：

                                                              

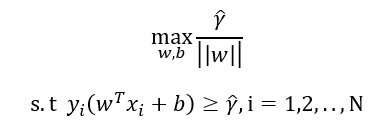
因为函数间隔和w,b是成正比的，可以将函数间隔设为1：

                                                                  

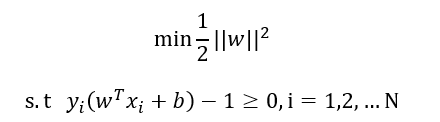
对于上述带不等式约束的优化使用广义拉格朗日函数进行无约束转换：

                                    

具体地说：

                                      

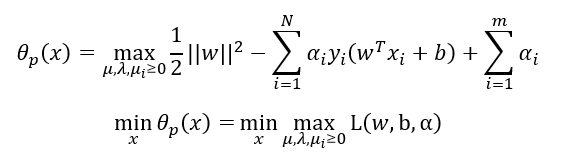
然后就是强对偶条件：

                                          

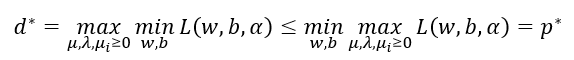
先对目标函数关于w,b进行优化

                                                      

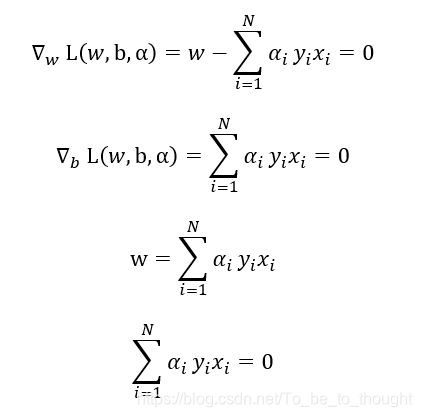
将等式条件代入：

                               

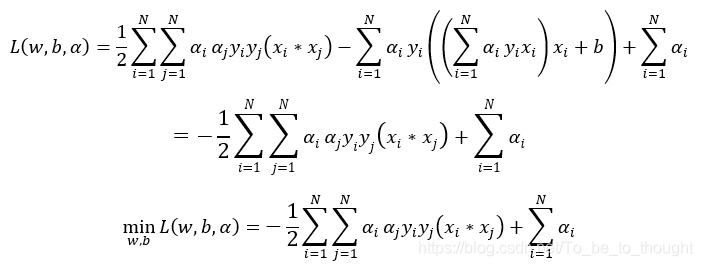
最终将问题转为关于拉格朗日系数的优化问题：

                                        

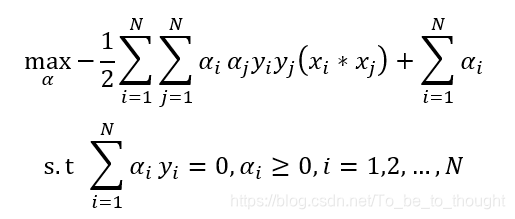
也就是：

                                                       

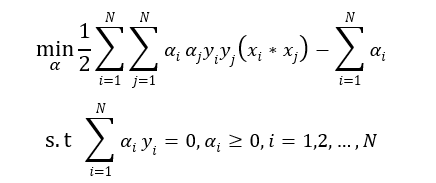
Hard margin要求数据线性可分，而soft margin允许少部分样本点在margin内部，margin内部的这些样本点对目标函数的损失需要定量的刻画。

0/1损失函数（不连续）：

                                                                    

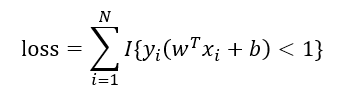
距离损失函数：

                                                    

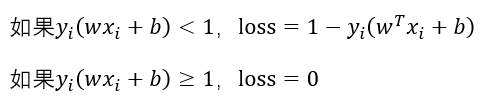
合在一起写为：

                                                                    

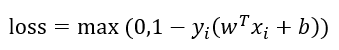
因此soft margin的优化目标函数写为：

                                             

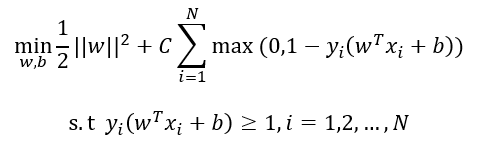
令

                                                  

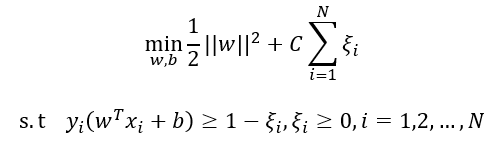
然后按照hard margin进行无约束转换和KKT对偶转换即可。

参考文献：《统计学习方法》