【题型总结】数位dp

数位动态规划

数位DP介绍

• 可以解决的问题

  对于「数位 DP」题，都存在「询问[a, b]（a 和 b 均为正整数，且 a<b）区间内符合特定条件的数值个数为多少」的一般形式，通常我们需要实现一个查询 [0,x] 有多少合法数值的函数 f(int x)，然后应用「容斥原理」求解出 [a,b] 的个数：f(b)−f(a−1)

  • 这个区间可能很大，暴力代码一般会超时，此时就可以使用数位DP解决该类问题。

  • 由于数位是按位dp，数的大小对复杂度的影响很小，时间复杂度为状态个数 * 单个状态的转移次数

• 模板题

  试计算在区间 1到 n的所有整数中，数字 x（0≤x≤9）共出现了多少次？例如，在 1 到 11 中，即在 1,2,3,4,5,6,7,8,9,10,11 中，数字 1出现了 4次。

• 模板

  • 首先将 $n$ 转换成字符串 $s$，定义 $f(i,condition,isLimit,isNum)$ 表示构造从左往右第 $i$ 位及其之后数位中的 满足特定条件的个数，其余参数的含义为：

    • $i$表示当前构造至从左往右第$i$位

    • $condition$表示与特定条件相关的变量或者计数

    • $isLimit$ 表示当前是否受到了 $n$的约束。若为真，则第 $i$ 位填入的数字至多为 $s[i]$，否则可以枚举至 最大值。如果在受到约束的情况下填了 $s[i]$，那么后续填入的数字仍会受到 $n$的约束。

      • 取决于第$i-1$位填充是否受限，以及当前填充的数是否达到上限值

    • $isNum$ 表示 $i$前面的数位是否填了数字。若为假，则当前位可以跳过（不填数字），或者要填入的数字至少为 $1$；若为真，则要填入的数字可以从 $0$开始。是否需要isNum取决于前导0对结果是否有影响

  • 实现

    • $dp$数组的含义为在不受到约束时，第$i$位枚举值固定时的合法方案数
    • 在实现过程中 Java/C++/Go 只需要记忆化 $(i,condition)$ 这个状态，因为：
      1. 对于一个固定的 $(i,condition)$，这个状态受到 isLimit或者isNum的约束在整个递归过程中至多会出现一次，没必要记忆化。
      2. 另外，如果只记忆化 $(i,condition)$，$dp$ 数组的含义就变成在不受到约束时的合法方案数，所以要在 !isLimit&&isNum成立时才去记忆化。

  作者：灵茶山艾府
  链接：https://leetcode.cn/problems/number-of-digit-one/solutions/1750339/by-endlesscheng-h9ua/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

相关题目

1.数字1的个数【LC233】

2022/11/25

给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。

• 思路：数位dp

  首先将 $n$ 转换成字符串 $s$，定义 $f(i,cnt1,isLimit,isNum)$ 表示构造从左往右第 $i$ 位及其之后数位中的 1 的个数，其余参数的含义为：

  • $i$表示当前构造至从左往右第$i$位

  • $cnt1$表示第$0$位至第$i-1$位填了多少个 $1$

  • $isLimit$ 表示当前是否受到了 $n$的约束。若为真，则第 $i$ 位填入的数字至多为 $s[i]$，否则可以枚举至 9。如果在受到约束的情况下填了 $s[i]$，那么后续填入的数字仍会受到 $n$的约束。

    • 取决于第$i-1$位填充是否受限，以及当前填充的数是否达到上限值

  • $isNum$ 可以忽略对于本题来说，由于前导零对答案无影响，isNum可以省略

  那么 $f(0,0,true)$ 即为最终结果

• 实现

  • 首先将$n$转化为字符串数组s，存储高位至低位的数值大小，会影响isLimit
  • 然后使用$dp$数组记录在不受到约束时，第$i$位枚举值固定时的合法方案数，即从左往右第$i$位之后所有枚举数中1的个数【不包括第$i$位】
  • 然后通过for循环，枚举每一位其所有可能的值

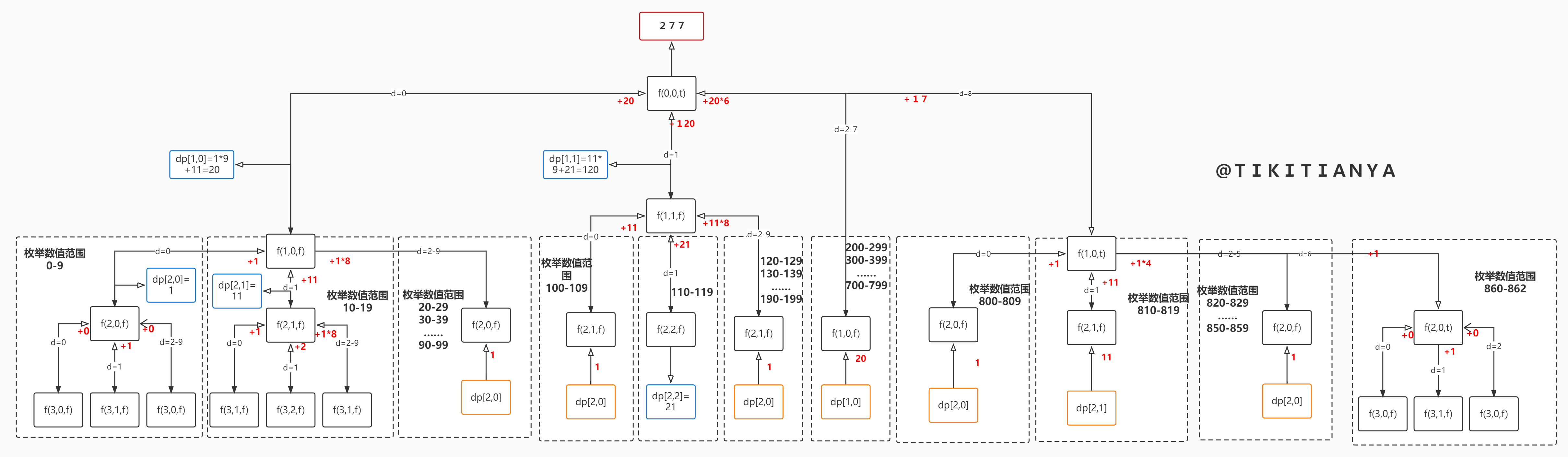
• 举例说明：计算所有小于等于 n 的非负整数中数字 1 出现的个数。

  如果当前的枚举数不受限，并且状态$dp[i,cnt1]$之前已经计算过，那么此时第$i$位枚举值固定时的合法方案数不需要重新计算，直接返回$dp[i,cnt1]$即可

  

• 代码

  class Solution {
      char s[];
      int dp[][];
  
      public int countDigitOne(int n) {
          s = Integer.toString(n).toCharArray();
          int m = s.length;
          dp = new int[m][m];
          for (int i = 0; i < m; i++) Arrays.fill(dp[i], -1);
          return f(0, 0, true);// 第i位受isLimit约束
      }
  
      int f(int i, int cnt1, boolean isLimit) {
          if (i == s.length) return cnt1;
          if (!isLimit && dp[i][cnt1] >= 0) return dp[i][cnt1];
          int res = 0; // 记录从左往右第i+1位之后所有枚举数中1的个数
          for (int d = 0, up = isLimit ? s[i] - '0' : 9; d <= up; ++d)
              // d代表枚举要填入的数字 up代表上限值 不受限则为9 受限则为第i位的值
              // 以下代码运用到了回溯
              // 具体含义为：寻找从左往右第i+1为以及之后数位中1的个数，因此需要更新cnt1以及isLimit
              // cnt1含义为前面i位填充1的个数，因此如果当前位填入的数字为i，那么cnt1 + 1,否则加0
              // isLimit含义为该位填充数字是否受限，取决于前一次填充是否受限，以及当前填充是否达到up
              res += f(i + 1, cnt1 + (d == 1 ? 1 : 0), isLimit && d == up);
          if (!isLimit) dp[i][cnt1] = res;// dp数组的含义为在不受到约束时第i位的合法方案数，即从左往右第i位之后所有枚举数中1的个数【不包括第i位】
          return res;
      }
  }
  
  

  • 复杂度

    • 时间复杂度：$O(logn)$，$\lceil log_{10}n \rceil+1 $为数字的位数，时间复杂度 = 状态个数 * 单个状态的转移次数，状态个数就是 dp 数组的长度，即 $O(logn)$，而单个状态的转移次数 = O(2) = O(1)，所以时间复杂度为 $O(logn)$
    • 空间复杂度：$O(logn)$

2.不含连续1的非负整数【LC600】

Given a positive integer n, return the number of the integers in the range [0, n] whose binary representations do not contain consecutive ones.

2022/11/25

同LC233的思路相同，区别在于把数使用二进制表示

• 思路：数位dp

  首先将 $n$ 转换成二进制int数组binary，定义 $f(i,pre,isLimit,isNum)$ 表示构造从左往右第 $i$ 位及其之后数位的合法方案数，即不存在连续1的个数，其余参数的含义为：

  • $i$表示当前构造至从左往右第$i$位

  • $pre$表示第$i-1$位填充的值

  • $isLimit$ 表示当前是否受到了 $n$的约束。若为真，则第 $i$ 位填入的数字至多为 $binary[i]$，否则可以枚举至 1。如果在受到约束的情况下填了 $s[i]$，那么后续填入的数字仍会受到 $n$的约束。

    • 取决于第$i-1$位填充是否受限，以及当前填充的数是否达到上限值

  • $isNum$ 可以忽略对于本题来说，由于前导零对答案无影响，isNum可以省略

  那么 $f(0,0,true)$ 即为最终结果

• 实现

  • 首先将$n$转化为二进制形式，并使用int数组binary存储
  • 然后使用$dp[i][j]$数组代表在不受到约束时，第$i$位枚举值固定为$j$时的，合法方案数，即从左往右第$i$位之后所有枚举数中不含1的个数【不包括第$i$位】
  • 然后对于每一位枚举其所有可能的值，由于枚举值只可能为0或者1，因此可以不使用for循环，直接判定
    • 如果不受限并且前一位不为1并且最大值为0，那么第$i$位可以填充1
    • 任何情况均可以填充0

• 代码

  class Solution {
      int [] binary;
      int[][] dp;
      public int findIntegers(int n) {
          int m = 32;        
          binary = new int[m];// 转化为二进制数组
          for (int i = 0; i < m; i++){
              binary[i] = (n >> (31-i)) & 1;
          }        
          dp = new int[m][2];
          for (int i = 0; i < m; i++){
              Arrays.fill(dp[i],-1);
          }
          int i = 0;
          while (i < m && binary[i] == 0){// 找到第一个不为0的二进制
              i++;
          }
          return f(i,0,true);
      }
      public int f(int i, int pre, boolean isLimit){
          if (i == binary.length){
              return 1;
          }
          if (!isLimit && dp[i][pre] >= 0){// 不受限 并以及计算过
              return dp[i][pre];
          }
          int res = 0;// 记录第i位之后的枚举可能性
          int up = isLimit ? binary[i] : 1;// 
          res += f(i + 1, 0, isLimit && up == 0);// 第i+1位填0 
          if (pre != 1 && up == 1){
              res += f(i + 1, 1, isLimit);// 第i位填1
          }               
          if (!isLimit){
              dp[i][pre] = res;
          }
          return res;
          
      }    
  }
  

  • 复杂度

    • 时间复杂度：$O(logn)$，$\lceil log_{10}n \rceil+1 $为数字的位数，时间复杂度 = 状态个数 * 单个状态的转移次数，状态个数就是 dp 数组的长度，即 $O(logn)$，而单个状态的转移次数 = O(10) = O(1)，所以时间复杂度为 $O(logn)$
    • 空间复杂度：$O(logn)$

3.统计各位数字都不同的数字个数【LC357】

Given an integer n, return the count of all numbers with unique digits, x, where 0 <= x < 10ⁿ.

排列组合

2022/11/27

• 思路：根据排列组合原理，由于要求各位数字都不相同，因此每位数字可以选择的范围是一定的，最高位可选择的数值个数为 9，而从次高位开始到最低位，可选的个数从 9 开始逐一递减。因此使用乘法原理，每位数可选的数值个数相乘即是长度为 n的数的可能方案数 cur，而所有长度 [1,n] 的方案数累加即是答案。

  作者：宫水三叶
  链接：https://leetcode.cn/problems/count-numbers-with-unique-digits/solutions/1411205/by-ac_oier-6tfl/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

• 实现

  class Solution {
      public int countNumbersWithUniqueDigits(int n) {
          if (n == 0){
              return 1;
          }
          int res = 10;
          int last = 9;// 最高位可以选择的数字个数
          int choice = 9;// 次高位可以选择的数字个数 然后依次减1
          for (int i = 2; i <= n; i++){
              int cur = last * choice;
              res += cur;
              last = cur;
              choice--;
          }
          return res;
      }
  }
  

  • 复杂度

    • 时间复杂度：$O(n)$
    • 空间复杂度：$O(1)$

数位dp

2022/11/28

• 题目升级：回答任意区间$[l,r]$ 内合法数的个数。

• 思路：数位dp

  首先将 $n$ 转换成字符串 $s$，定义 $f(i,mask,isLimit,isNum)$ 表示构造从左往右第 $i$ 位及其之后数位的合法方案数，即各位数字都不同的数字个数，其余参数的含义为：

  • $i$表示当前构造至从左往右第$i$位

  • $mask$表示前面选过的数字集合，换句话说，第 $i$ 位要选的数字不能在 $mask$中。

    • 用低十位表示数字 [0,9] 是否被使用**(int 变量）**

  • $isLimit$ 表示当前是否受到了 $n$的约束。若为真，则第 $i$ 位填入的数字至多为 $s[i]$，否则可以枚举至 9。如果在受到约束的情况下填了 $s[i]$，那么后续填入的数字仍会受到 $n$的约束。

    • 取决于第$i-1$位填充是否受限，以及当前填充的数是否达到上限值

  • $isNum$ 表示 $i$前面的数位是否填了数字。若为假，则当前位可以跳过（不填数字），或者要填入的数字至少为 $1$；若为真，则要填入的数字可以从 $0$开始。

    • 在本题中，不允许前导0的存在，因此本题需要参数isNum

  那么 $f(0,0,true,false)$ 即为最终结果

• 实现

  • 首先位数$n$对应的数值最大值为$10^n-1$，将其存入字符数组s，存储高位至低位的数值大小，会影响isLimit【本题需要判断的数值范围为**[0,10^n-1]**】

  • 然后使用$dp$数组记录在不受到约束时，第$i$位枚举范围固定时的合法方案数，即从左往右第$i$位之后所有数位不相同的数字个数【不包括第$i$位】

  • 如果不受限并且前一位是数值，那么可以查询是否已经计算过第$i$位枚举范围一定时的合法方案数，若dp[i][mask] >= 0，则表示已经计算过，可直接返回

    • 比如当n=4时，枚举范围为0-9999，12XX和21XX的合法方案数相同，可直接查询得到

  • 否则枚举第$i$位的可能性【既可以填入数字，也可以不填入数字】

    • 不填入数字：如果isNum为false，那么第$i$位也可以不填入数字

      此时对结果的贡献为f(i+1,mask,false,false)

    • 填入数字：通过for循环，枚举每一位其所有可能的值d

      1. 初始值：可能为0或者1
         • isNum为true即前一位为数字时，那么第$i$位可以从0开始枚举
         • 否则，只有最低位可以从0开始枚举，其他位均从1开始枚举【LC1012 最低位也从1开始枚举】
      2. 上限值：由limit决定
         • 如果受限，那么枚举的最大值为s[i]
      3. 只有d不在mask中时，才对结果有贡献，共享为f(i+1,mask | d,isLimit && d==up,true)

  • 如果不受限并且前一位为数值，那么记录result至dp数组中

• 代码

  class Solution {
      char[] s;
      int[][] dp;
      public int countNumbersWithUniqueDigits(int n) {
          int num = (int)(Math.pow(10,n) - 1);
          s = Integer.toString(num).toCharArray();
          int len = s.length;
          dp = new int[len][1 << 10];
          for (int i = 0; i < len;i++){
              Arrays.fill(dp[i],-1);
          }
          return f(0, 0, true, false);
      }
      //最小值为0
      int f(int i, int mask, boolean isLimit, boolean isNum) {
         if (i == s.length) {
             return isNum ? 1 : 0;
         }
         if (!isLimit && isNum && dp[i][mask] >= 0){
             return dp[i][mask];
         }
         int res = 0;
         // isNum为false 可不填
         if (!isNum){
             res += f(i + 1, mask, false, false);
         }
         int up = isLimit ? s[i] - '0' : 9;
         for (int d = isNum || i == s.length - 1 ? 0 : 1;d <= up; d++){
             if ( (mask >> d & 1) == 0){
                 res += f(i + 1, mask | (1 << d),isLimit && d == up, true);
             }
         }
         if (!isLimit && isNum){
             dp[i][mask] = res;
         }
         return res;
      }
  }
  

  • 复杂度

    • 时间复杂度：$O(n)$，$n$为数字的位数，时间复杂度 = 状态个数 * 单个状态的转移次数，状态个数就是 dp 数组的长度，即 $O(n)$，而单个状态的转移次数 = O(10) = O(1)，所以时间复杂度为 $O(n)$
    • 空间复杂度：$O(n)$

4.至少有1位重复的数字【LC1012】

Given an integer n, return the number of positive integers in the range [1, n] that have at least one repeated digit.

2022/11/28

• 思路：将题目转化为[1,n]范围内所有数的个数减去各位数字都不同的数字个数，因此可采用同统计各位数字都不同的数字个数【LC357】相同的数位dp思路，只需将最低位的枚举数值改为从1开始即可

• 代码

  class Solution {
      char s[];
      int dp[][];
  
      public int numDupDigitsAtMostN(int n) {
          s = Integer.toString(n).toCharArray();
          var m = s.length;
          dp = new int[m][1 << 10];
          for (var i = 0; i < m; i++) Arrays.fill(dp[i], -1);
          return n - f(0, 0, true, false);
      }
      // 最小值为1
      int f(int i, int mask, boolean isLimit, boolean isNum) {
          if (i == s.length) return isNum ? 1 : 0;// 前一位为数字才有合法数字
          if (!isLimit && isNum && dp[i][mask] >= 0) return dp[i][mask];
          var res = 0;
          if (!isNum) res = f(i + 1, mask, false, false); // 前一位不是数字 那么可以跳过当前数位
          // 前一位为数字，那么第i位可以从0开始枚举；否则，均从1开始枚举【与LC357的区别，合法数的范围为[1,n]】
          for (int d = isNum ? 0 : 1, up = isLimit ? s[i] - '0' : 9; d <= up; ++d) // 枚举要填入的数字 d
              if ((mask >> d & 1) == 0) // d 不在 mask 中
                  // mask | (1 << d) 将mask的第d位赋值为1
                  res += f(i + 1, mask | (1 << d), isLimit && d == up, true);
          if (!isLimit && isNum) dp[i][mask] = res;
          return res;
      }
  }
  
  作者：灵茶山艾府
  链接：https://leetcode.cn/problems/numbers-with-repeated-digits/solutions/1748539/by-endlesscheng-c5vg/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  

  • 复杂度

    • 时间复杂度：$O(logn)$，n为数字的位数，时间复杂度 = 状态个数 * 单个状态的转移次数，状态个数就是 dp 数组的长度，即 $O(logn)$，而单个状态的转移次数 = O(10) = O(1)，所以时间复杂度为 $O(logn)$
    • 空间复杂度：$O(logn)$

5.最大为N的数字组合【LC902】

Given an array of digits which is sorted in non-decreasing order. You can write numbers using each digits[i] as many times as we want. For example, if digits = ['1','3','5'], we may write numbers such as '13', '551', and '1351315'.

Return the number of positive integers that can be generated that are less than or equal to a given integer n.

2022/11/29 终于自己做出来了！！！！！

• 思路：数位dp，与其他题目不同的是，每位的数字只能在数组digits内选，因此使用mask记录digits内的数字，并用位运算判断当前数字是否可以使用

  首先将 $n$ 转换成字符串 $s$，定义 $f(i,mask,isLimit,isNum)$ 表示构造从左往右第 $i$ 位及其之后数位的合法方案数，即各位数字都不同的数字个数，其余参数的含义为：

  • $i$表示当前构造至从左往右第$i$位

  • $mask$表示可以选则的数字集合，换句话说，第 $i$ 位可以选择的数字在 $mask$中。

    • 用低十位表示数字 [0,9] 能否被使用**(int 变量）**

  • $isLimit$ 表示当前是否受到了 $n$的约束。若为真，则第 $i$ 位填入的数字至多为 $s[i]$，否则可以枚举至 9。如果在受到约束的情况下填了 $s[i]$，那么后续填入的数字仍会受到 $n$的约束。

    • 取决于第$i-1$位填充是否受限，以及当前填充的数是否达到上限值

  • $isNum$ 表示 $i$前面的数位是否填了数字。若为假，则当前位可以跳过（不填数字），或者要填入的数字至少为 $1$；若为真，则要填入的数字可以从 $0$开始。

    • 在本题中，不允许前导0的存在，因此本题需要参数isNum

  那么 $f(0,0,true,false)$ 即为最终结果

• 实现

  • 首先将字符串$n$对应的数值存入字符数组s，存储高位至低位的数值大小，会影响isLimit【本题需要判断的数值范围为**[1,n]**】

  • 然后使用$dp$数组记录在不受到约束时，第$i$位枚举范围固定时的合法方案数，即从左往右第$i$位之后所有数字个数【不包括第$i$位】【由于mask为固定值，因此dp为一维数组即可存储】

  • 如果不受限并且前一位是数值，那么可以查询是否已经计算过第$i$位枚举范围一定时的合法方案数，若dp[i] >= 0，则表示已经计算过，可直接返回

  • 否则枚举第$i$位的可能性【既可以填入数字，也可以不填入数字】

    • 不填入数字：如果isNum为false，那么第$i$位也可以不填入数字

      此时对结果的贡献为f(i+1,mask,false,false)

    • 填入数字：通过for循环，枚举每一位其所有可能的值d

      1. 初始值：可能为0或者1
         • isNum为true即前一位为数字时，那么第$i$位可以从0开始枚举
         • 否则，均从1开始枚举
      2. 上限值：由limit决定
         • 如果受限，那么枚举的最大值为s[i]
      3. 只有d在mask中时，才对结果有贡献，共享为f(i+1,mask,isLimit && d==up,true)

  • 如果不受限并且前一位为数值，那么记录result至dp数组中

• 代码

  class Solution {
      char[] s;
      int[] dp;
      public int atMostNGivenDigitSet(String[] digits, int n) {
          s = Integer.toString(n).toCharArray();
          int m = s.length;
          dp = new int[m + 1];
          Arrays.fill(dp, -1);
          int mask = 0;
          for (int i = 0; i < digits.length; i++){
              int d = digits[i].toCharArray()[0] - '0';
              mask |= 1 << d;
          }
          return f(0,mask,true,false);
      }
      public int f(int i, int mask, boolean isLimit,boolean isNum){
          if (i == s.length) return isNum ? 1 : 0;
          if (!isLimit && isNum && dp[i] >= 0) return dp[i];
          int res = 0;
          if (!isNum){
              res += f(i + 1, mask, false, false);
          }
          for (int d = isNum ? 0 : 1, up = isLimit ? s[i] - '0' : 9; d <= up; d++){
              if ((mask >> d & 1) == 1){// d在mask中
                  res += f(i + 1, mask, isLimit && d == up, true);
              }
          }
          if (!isLimit && isNum){
              dp[i] = res;
          }
          return res;
      }
  }
  

  • 复杂度

    • 时间复杂度：$O(logn)$，$\lceil log_{10}n \rceil+1 $为数字的位数，时间复杂度 = 状态个数 * 单个状态的转移次数，状态个数就是 $dp$ 数组的长度，即 $O(logn)$，而单个状态的转移次数 = O(10) = O(1)，所以时间复杂度为 $O(logn)$
    • 空间复杂度：$O(logn)$，即为动态规划中存储状态需要使用的空间。

6.旋转数字【LC788】

An integer x is a good if after rotating each digit individually by 180 degrees, we get a valid number that is different from x. Each digit must be rotated - we cannot choose to leave it alone.

A number is valid if each digit remains a digit after rotation. For example:

• 0, 1, and 8 rotate to themselves,
• 2 and 5 rotate to each other (in this case they are rotated in a different direction, in other words, 2 or 5 gets mirrored),
• 6 and 9 rotate to each other, and
• the rest of the numbers do not rotate to any other number and become invalid.

Given an integer n, return the number of good integers in the range [1, n].

数位dp

2022/11/29 终于自己做出来了！！！！！

• 思路：数位dp，与LC902有点相似，但略复杂点，每位的数字只能在$\lceil$可旋转的数字$\rfloor$rotate=0,1,2,5,6,8,9内选，并且只有当某一位数字包含数字good=2,5,6,9任意一个时，该数字才是$\lceil$好数：经过旋转后与原数不相等$\rfloor$

  首先将 $n$ 转换成字符串 $s$，定义 $f(i,isGood,isLimit,isNum)$ 表示构造从左往右第 $i$ 位及其之后数位的合法方案数，即各位数字都不同的数字个数，其余参数的含义为：

  • $i$表示当前构造至从左往右第$i$位

  • $isGood$ 表示前$i$位数位是否为好数，只要前$i$位数字包含数组good=2,5,6,9中一个以上数字即为好数。使用int变量表示，不是好数时为0，是好数时为1。

    • 由于数字可以重复选取，因此前$i$位包含几个好数，不会影响后$i$位的合法方案数，因此只需要记录包含或者不包含即可

  • $isLimit$ 表示当前是否受到了 $n$的约束。若为真，则第 $i$ 位填入的数字至多为 $s[i]$，否则可以枚举至 9。如果在受到约束的情况下填了 $s[i]$，那么后续填入的数字仍会受到 $n$的约束。

    • 取决于第$i-1$位填充是否受限，以及当前填充的数是否达到上限值

  • $isNum$ 表示 $i$前面的数位是否填了数字。若为假，则当前位可以跳过（不填数字），或者要填入的数字至少为 $1$；若为真，则要填入的数字可以从 $0$开始。

    • 在本题中，有无前导0均不影响结果的，因此本题可以不需要参数isNum

  在本题中需要记录的状态是$dp[i][isGood]$， $f(0,0,true,false)$ 即为最终结果

• 实现

  • 首先将字符串$n$对应的数值存入字符数组s，存储高位至低位的数值大小，会影响isLimit【本题需要判断的数值范围为**[1,n]**】

  • 然后使用$dp$数组记录在不受到约束时，第$i$位枚举值固定时的合法方案数，即从左往右第$i$位之后所有数字个数【不包括第$i$位】【由于isGood只有两种值，因此使用二维数组存储】

  • 如果不受限，那么可以查询是否已经计算过第$i$位枚举范围一定时的合法方案数，若dp[i][isGood] >= 0，则表示已经计算过，可直接返回

  • 否则枚举第$i$位的可能性

    • 通过for循环，枚举每一位其所有可能的值d

      1. 初始值：从0开始枚举
      2. 上限值：由limit决定
         • 如果受限，那么枚举的最大值为s[i]-'0'
      3. 只有d在0,1,2,5,6,8,9中时，才对结果有贡献，贡献为f(i+1,isGood,isLimit && d==up)
         • 若存在2,5,6,9，那么isGood为1
         • 不存在2,5,6,9，那么isGood为0

  • 如果不受限，那么记录result至dp数组中

• 代码

  class Solution {
      char[] s;
      int[][] dp;
      public int rotatedDigits(int n) {
          s = Integer.toString(n).toCharArray();
          int m = s.length;
          dp = new int[m][2];
          for (int i = 0; i < dp.length; i++){
              Arrays.fill(dp[i], -1);
          }
          return f(0, 0, true, false);
      }
      public int f(int i, int isGood, boolean isLimit,boolean isNum){
          if (i == s.length) return isGood == 1 && isNum ? 1 : 0;
          if (!isLimit && isNum && dp[i][isGood] > -1) return dp[i][isGood];
          int res = 0;
          if (!isNum){`
              res += f(i + 1, isGood, false, false);
          }
          int up = isLimit ? s[i] -'0' : 9;
          for (int d = isNum ? 0 : 1; d <= up; d++){
              if (d == 0 || d == 1 || d == 8){
                  res += f(i + 1, isGood, isLimit && d == up, true);
              }else if (d == 2 || d == 5 || d == 6 || d == 9){
                  res += f(i + 1, 1, isLimit && d == up, true);
              }
          }
          if (!isLimit && isNum) dp[i][isGood] = res;
          return res;
      }
  }
  

  • 复杂度

    • 时间复杂度：$O(logn)$，$\lceil log_{10}n \rceil+1 $为数字的位数，时间复杂度 = 状态个数 * 单个状态的转移次数，状态个数就是 $dp$ 数组的长度，即 $O(logn)$，而单个状态的转移次数 = O(10) = O(1)，所以时间复杂度为 $O(logn)$
    • 空间复杂度：$O(logn)$，即为动态规划中存储状态需要使用的空间。