堆排序与PriorityQueue

最新推荐文章于 2025-11-24 19:09:20 发布

原创

最新推荐文章于 2025-11-24 19:09:20 发布 · 1.5k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #堆排列 #PriorityQueue

堆是一种非线性结构，常用于实现优先队列。堆排序利用堆的特性进行排序，时间复杂度为O(NlogN)。Java中的PriorityQueue通过小顶堆实现，保证每次取出的元素是最小的。PriorityQueue提供了add、offer、element、peek、remove等方法，插入和删除元素时会自动调整堆结构以保持堆属性。

在做leetcode时碰到了应用PriorityQueue，巩固一下相关知识

堆
PriorityQueue
手写Heap

堆

堆是一种非线性结构，可以把堆看作一个数组，也可以被看作一个完全二叉树。堆其实就是利用完全二叉树的结构来维护的一维数组，按照堆的特点可以把堆分为大顶堆和小顶堆。堆的这种特性非常的有用，堆常常被当做优先队列使用，因为可以快速的访问到“最重要”的元素。
构建堆的过程，O（N）(调用一次)
堆排序，每次交换堆顶的元素和结尾的元素，调整堆，每次O（logN）
堆插入，每次将元素放在结尾，将结尾元素向上查找更大或更小的元素下沉，每次O（logN）

大顶堆：每个结点的值都大于或等于其左右子结点的值
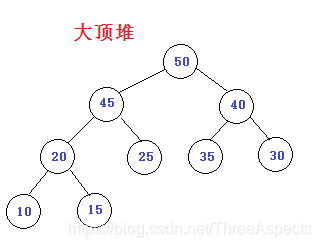
在这里插入图片描述
小顶堆：每个结点的值都小于或等于其左右子结点的值

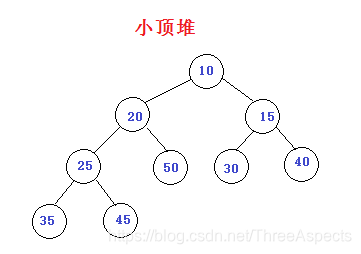
【堆和普通树的区别】
1、内存占用：普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配额外的内存。堆仅仅使用数组，且不使用指针。
2、平衡：二叉搜索树必须是“平衡”的情况下，其大部分操作的复杂度才能达到O(nlog2n)。可以按任意顺序位置插入/删除数据，或者使用 AVL 树或者红黑树，但是在堆中实际上不需要整棵树都是有序的。
3、搜索：在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作。
【堆排序的过程】
堆排序的基本思想：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值，如此反复执行，便能得到一个有序序列了，建立最大堆时是从最后一个非叶子节点开始从下往上调整的。升序----使用大顶堆；降序----使用小顶堆。

/* Function: 构建大顶堆 */
void BuildMaxHeap(int[] heap, int len)
{
   
   
    int i，temp;
    for (i = len/2-1; i >= 0; i--)
    {
   
   
        if ((2*i+1) < len && heap[i] < heap[2*i+1])    /* 根节点大于左子树 */
        {
   
   
            temp = heap[i];
            heap[i] = heap[2*i+1];
            heap[2*i+1] = temp;
            /* 检查交换后的左子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
            if ((2*(2*i+1)+1 < len && heap[2*i+1] < heap[2*(2*i+1)+1]) || (2*(2*i+1)+2 < len && heap[2*i+1] < heap[2*(2*i+1)+2]))
            {
   
   
                BuildMaxHeap(heap, len);
            }
        }
        if ((2*i+2) < len && heap[i] < heap[2*i+2])    /* 根节点大于右子树 */
        {
   
   
            temp = heap[i];
            heap[i] = heap[2*i+2];
            heap[2*i+2] = temp;
            /* 检查交换后的右子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
            if ((2*(2*i+2)+1 < len && heap[2*i+2] < heap