一、载流圆环线圈的磁场分布互感计算
1.公式推导:

2. MATLAB程序:
(1)一维:
clc
I=1;u0=4*pi*1e-7;K0=I*u0/4/pi;
a=input('输入线圈半径:');
X=input('输入x轴范围:');Y=input('输入y轴取值:');Z=input('输入z轴取值:');
N=1000;
dj=2*pi/N;
Bx=0;By=0;Bz=0;
for n=0:N
j=n*2*pi/N;
r=sqrt((X-a*cos(j)).^2+(Y-a*sin(j)).^2+Z.^2);
r3=r.^3;
Bx=Bx+K0.*dj.*a.*Z.*cos(j)./r3;
By=By+K0.*dj.*a.*Z.*sin(j)./r3;
Bz=Bz+K0.*dj.*a.*(a-Y.*sin(j)-X.*cos(j))./r3;
end
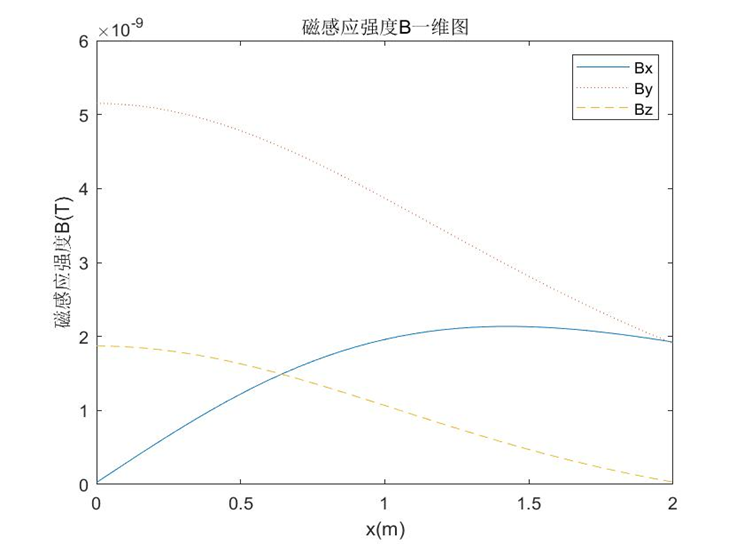
plot(X,Bx);hold on;plot(X,By,':');plot(X,Bz,'--');
xlabel('x(m)');ylabel('磁感应强度B(T)');
legend('Bx','By','Bz');title('磁感应强度B一维图');
(2)二维
clear all;
figure(1);
a=input('输入线圈半径;');X=input('输入x轴取值:');Y=input('输入y轴范围:');
Z=input('输入z轴范围:');
the=0:pi/20:2*pi;I=1;u0=4*pi*1e-7;K0=I*u0/4/pi;
[Y,Z,T]=meshgrid(Y,Z,the);
r=sqrt((X-a*cos(T)).^2+Z.^2+(Y-a*sin(T)).^2);
r3=r.^3; dby=a*Z.*sin(T)./r3;
by=K0*trapz(dby,3);dbz=a*(a-Y.*sin(T)-X.*cos(T))./r3;
bz=K0*trapz(dbz,3);
subplot(121);
[bSY,bSZ]=meshgrid([0:0.05:0.2],0);
h1=streamline(Y(:,:,1),Z(:,:,1),by,bz,bSY,bSZ,[0.1,1000]);
h2=copyobj(h1,gca); rotate(h2,[1,0,0],180,[0,0,0]);
h3=copyobj(allchild(gca),gca); rotate(h3,[0,1,0],180,[0,0,0]);
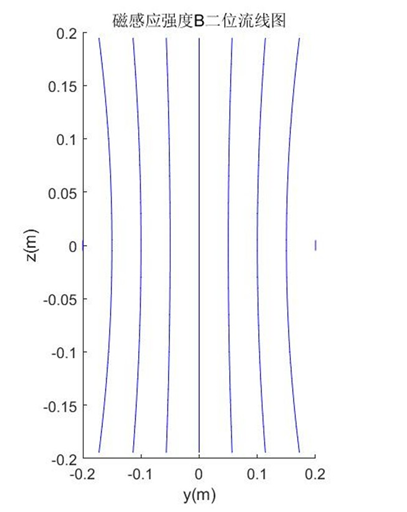
xlabel('y(m)'); ylabel('z(m)'); title('磁感应强度B二位流线图');
for kk=1:4
[bSY,bSZ]=meshgrid(0.2+kk*0.02,0);
streamline(Y(:,:,1),Z(:,:,1),by,bz,bSY,bSZ,[0.02/(kk+1),4500]);
end
(3)三维
clc;
a=0.3; I=1; u0=4*pi*1e-7; K0=I*u0/4/pi;
[X,Y,Z]=meshgrid(-0.5:0.04:0.5);
N=100;
dj=2*pi/N;
Bx=0; By=0; Bz=0;
for n=0:N
j=n*2*pi/N;
r=sqrt((X-a*cos(j)).^2+(Y-a*sin(j)).^2+Z.^2);
r3=r.^3;
Bx=Bx+K0.*dj.*a.*Z.*cos(j)./r3;
By=By+K0.*dj.*a.*Z.*sin(j)./r3;
Bz=Bz+K0.*dj.*a.*(a-Y.*sin(j)-X.*cos(j))./r3;
end
t=0:pi/100:2*pi;
v=[-0.2,-0.1,0,0.1,0.2];
[Vx,Vy,Vz]=meshgrid(v,v,0);
plot3(Vx(:),Vy(:),Vz(:),'r*');hold on;
streamline(X,Y,Z,Bx,By,Bz,Vx,Vy,Vz,[0.01,2000]);hold on;
plot(a*exp(1i*t),'r-','LineWidth',3);hold on;
axis([-0.5,0.5,-0.5,0.5,-0.5,0.5]);
view(-35,45);
box on;
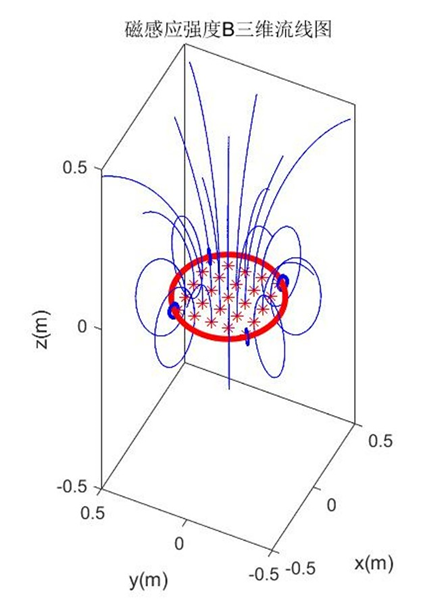
xlabel('x(m)');ylabel('y(m)');zlabel('z(m)');title('磁感应强度B三维流线图');
(4)互感计算
clc;
a=input('输入a线圈半径:');b=input('输入b线圈半径:'); x=input('输入x步长:');y=input('输入y步长:');d=input('输入线圈距离:');
u=4*pi*10^-7;N=1000;M=1000;i=1;Q=0;
l=sqrt(x.^2+y.^2);
for n=0:N
for m=0:N
j=n*2*pi/N; k=m*2*pi/M;
Q=Q+a.*b.*cos(j-k).*4.*pi.*pi./N./M./((a.^2+b.^2+d.^2+l.^2-2.*a.*b.*cos(j-k)+2.*y.*(b.*sin(j)-a.*sin(k))+2.*x.*(b.*cos(j)-a.*cos(k)))).^(1/2);
end
end
w=Q*u/(4*pi)/1e-8
3.结果展示

二、多边形线圈的互感计算
1.公式推导

2.结果展示:
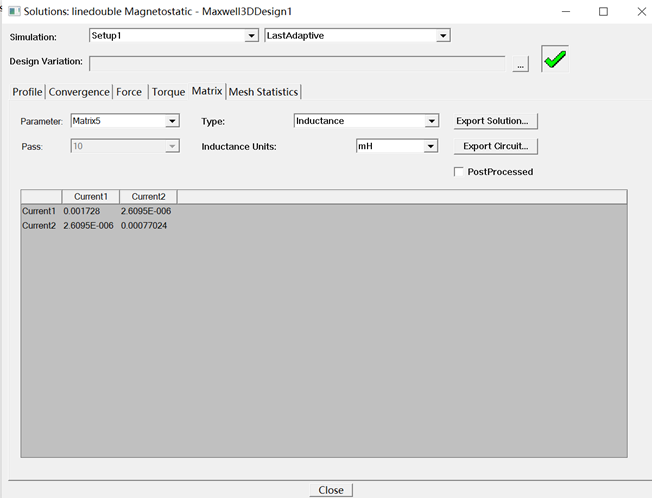
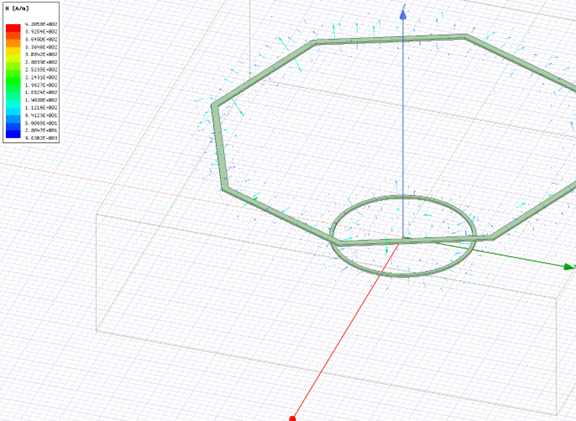








 MATLAB仿真载流与多边形线圈互感计算
MATLAB仿真载流与多边形线圈互感计算























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








