SDNU ACM-ICPC 2020 Competition For the End of Term(11-29)【解题报告】

前言

\quad 今天出了一坨锅，原因是出题组人手不够（没人验题…，求轻喷

说明

\quad 以下内容为现场赛时写的，一边看榜，一边写，所以是按照每道题被拿走FB的顺序写的。

题解

1644.Euler YYDS![找规律]

出题人：lhr \quad 验题人：ymf

\quad 全场最简单的题目，于 00:15:10 被 Visiter 拿走全场 First Blood！

题目大意

\quad $T(1\le T\le 10)$ 组数据，每组给一个整数 $n(1\le n\le 10^{100})$，问 $\phi (n)$ 的奇偶性.

分析

\quad 找规律可知：当 $n\ge 3$ 时 $\phi (n)$ 恒为偶数.

\quad 可使用更相减损之术：$\gcd (x,n)=gcd(n-x,n)$ 简单证明.

代码实现

#include <bits/stdc++.h>
using namespace std;

const int M = (int)1e2;

char n[M + 5];

void work()
{
   
   
	scanf("%s", n);
	puts(strcmp(n, "1") == 0 || strcmp(n, "2") == 0 ? "odd" : "even");
}

int main()
{
   
   
	// freopen("3.in", "r", stdin);
	// freopen("3.out", "w", stdout);
	int T; scanf("%d", &T);
	while(T--) work();
	return 0;
}

1649.Palindrome of prime number[模拟 + 暴力判断质数]

出题人：wx \quad 验题人：lhr

\quad 00:19:41 FB 诞生，By：18XiWenjuan

题目大意

$T(1\le T\le 10^5)$ 组数据，每组一个质数 $n(1\le n\le 10^5)$，问 $n$ 的回文数是否是质数.

分析

\quad 直接模拟 + 暴力循环 $[1, \sqrt{n}] $ 判断，事实证明这样不会 TLE.

代码实现

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

char n[20];

bool is_prime(ll n)
{
   
   
    for(int i = 2; 1ll * i * i <= n; ++i)
    {
   
   
        if(n % i == 0) return 0;
    }
    return 1;
}

void work()
{
   
   
    scanf("%s", n);
    int len = strlen(n);
    for(int i = len; i < 2 * len - 1; ++i) n[i] = n[2 * len - i - 2];
    ll m = 0;
    for(int i = 0; i < 2 * len - 1; ++i) m = m * 10 + n[i] - '0';
    puts(is_prime(m) ? "prime" : "noprime");
}

int main()
{
   
   
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    int T; scanf("%d", &T);
    while(T--) work();
    return 0;
}

1652.The Magic LMR Ring[找规律]

出题人：lhr \quad 验题人：

\quad 00:57:30 FB 诞生，By：2019jiyi

题目大意

\quad 求解大小为 $n$，间隔为 $1$ 的约瑟夫环.

分析

\quad 找规律可得

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
答案	1	1	3	1	3	5	7	1	3	5	7	9	11	13	15

\quad 答案显然.

\quad 证明：

\qquad 记 $f(n)$ 为大小为 $n$，间隔为 $1$ 约瑟夫环的答案.

\qquad 当 $n$ 为偶数时

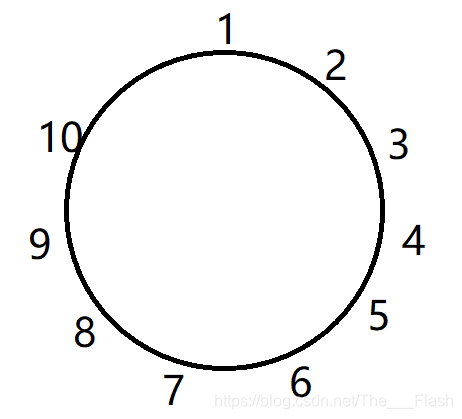
\qquad 删完一圈后发现，答案为 $2f(n/2)-1$.

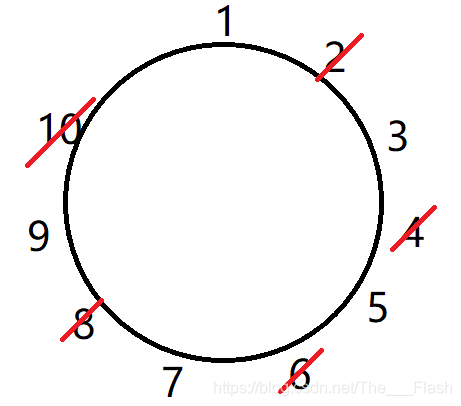
\qquad 当 $n$ 为奇数时

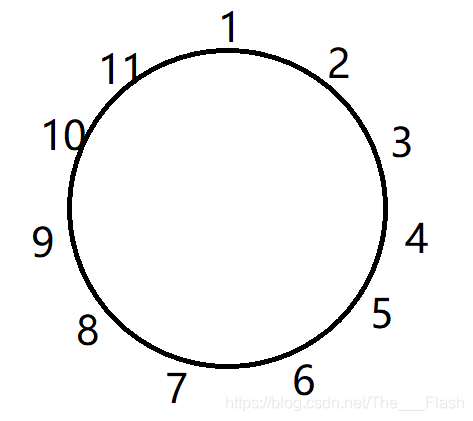
\qquad 删完一圈后发现，答案为 $2f(n/2)+1$.

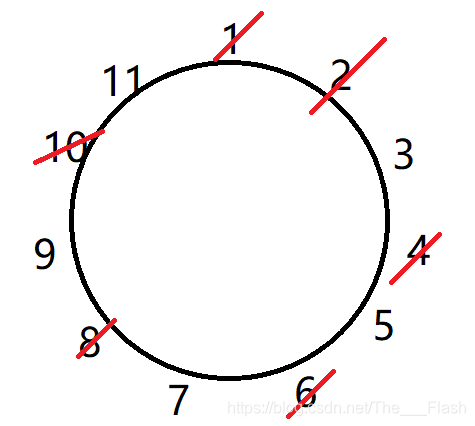
\qquad 分析到这里，使用递归即可 $AC$.

\qquad 剩下的部分留给读者自行证明.

代码实现

\quad 2019jiyiの代码

#include <queue>
#include <vector>
#include <set>
#include <stack>
#