本文探讨了基于增量信息的因子模型框架搭建，详细介绍了资本资产定价模型(CAPM)与套利定价模型(APT)，并讨论了均衡模型与统计模型的区别及应用。文中还对比了时间序列模型与横截面模型的特点。
-
因子模型系列之一：基于增量信息逐层解释的因子模型框架搭建
-
关键字
关键字 关键字 关键字 横截面模型 逐层增量解释的多因子检验 时间序列模型 因子暴露目标配置 经典均衡模型 统计模型 -
经典均衡模型
关于“均衡模型”，参见《理解资产定价领域的“均衡模型”：APT、CAPM、马歇尔、瓦尔拉斯、无套利均衡》
-
资本资产定价模型CAPM
1952年 H a r r y M a r k o w i t z Harry\;Markowitz HarryMarkowitz提出的分散投资与效率组合投资理论第一次以数理工具构建投资组合。其中最优投资组合需要计算协方差，受制于当时的计算能力，理论并未广泛运用到实践中。
1964年 W i l l i a m F . S h a r p e William \;F.Sharpe WilliamF.Sharpe等经济学家从实践角度提出了资本资产定价模型（ C a p i t a l A s s e t P r i c i n g M o d e l , C A P M Capital\;Asset\;Pricing\;Model,\;CAPM CapitalAssetPricingModel,CAPM）。其一般数学形式为：
E [ R S ] − r f = β S M ( E [ R M ] − r f ) E[R_S]-r_f=\beta^M_S(E[R_M]-r_f) E[RS]−rf=βSM(E[RM]−rf)
E [ R S ] E[R_S] E[RS]：投资组合 S S S的期望收益；E [ R M ] E[R_M] E[RM]：市场组合 M M M的期望收益；
β S M \beta^M_S βSM：市场组合的配置权重；
将公式(1)重写，现实意义会更清晰，其中令 w S M = β S M , w S f = 1 − β S M w^M_S=\beta^M_S,w^f_S=1-\beta^M_S wSM=βSM,wSf=1−βSM，得到新公式：
E [ R S ] = w S M ⋅ E [ R M ] + w S f r f E[R_S]=w^M_S\cdot E[R_M]+w^f_Sr_f E[RS]=wSM⋅E[RM]+wSfrf均衡条件下，投资组合的期望收益中，市场组合的配置权重为 w S M w^M_S wSM，无风险资产的配置权重为 w S f w^f_S wSf
-
套利定价模型APT
由套利定价理论得出的模型和资本资产定价模型一样，都是均衡模型。
套利定价理论（ A r b i t r a g e P r i c i n g T h e o r y , A P T Arbitrage\;Pricing\;Theory,APT ArbitragePricingTheory,APT）认为，资产的价格会受到多个因素的影响，这些
因素会影响资产的风险，从而改变资产的收益。
E [ R S ] − r f = ∑ j = 1 k β S j ( E [ R F j ] − r f ) E[R_S]-r_f=\sum^k_{j=1}\beta^j_S(E[R^j_F]-r_f) E[RS]−rf=j=1∑kβSj(E[RFj]−rf)
E [ R S ] E[R_S] E[RS]：资产 S S S的期望收益；E [ R F j ] E[R^j_F] E[RFj]：纯因素组合 j j j的期望收益；
跟上节内容一样，令 w S j = β S j , w S f = 1 − ∑ j = 1 k β S j w_S^j=\beta^j_S,w^f_S=1-\sum^k_{j=1}\beta^j_S wSj=βSj,wSf=1−∑j=1kβSj，得到：
E [ R S ] = ∑ j = 1 k w S j ⋅ E [ R F j ] + w S f r f E[R_S]=\sum^k_{j=1}w^j_S\cdot E[R^j_F]+ w^f_Sr_f E[RS]=j=1∑kwSj⋅E[RFj]+wSfrf均衡条件下，投资者持有一组纯因素组合与无风险资产，其中没想纯因素组合配置权重为 w S j , j = 1 , 2 , . . . , k w^j_S,j=1,2,...,k wSj,j=1,2,...,k，共配置 ∑ j = 1 k \sum^k_{j=1} ∑j=1k( w S j ⋅ 纯 因 素 组 合 j w^j_S \cdot 纯因素组合j wSj⋅纯因素组合j)，并持有权重为 w S f w^f_S wSf的无风险资产。
资本资产定价模型、套利定价理论模型，得出的模型都是均衡模型，描述了资产预期风险与预期收益率之间存在的线性关系。均衡模型构建了一种理想的状态，在这种理想状态下，每个投资者的行为都是可以被预测的。
然而，现实资本市场中基本不存在假设情况，也因此利用均衡模型在直接面向“未来、预期”的实证检验中存在困难。
在实证中，需要转换为
统计模型，来描述资产价格的决定因素，基于历史数据对均衡模型进行实证检验。
-
均衡模型
-
均衡模型与统计模型
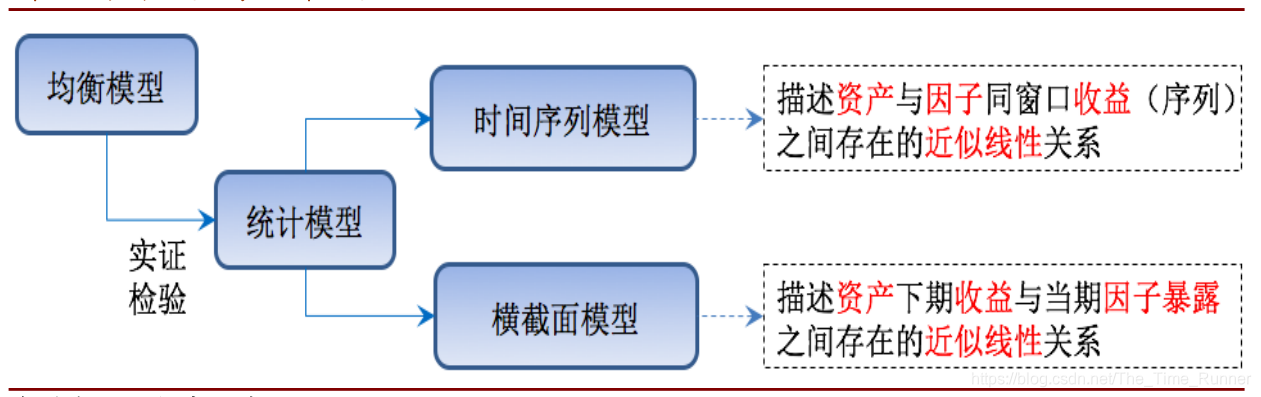
统计模型有两类基础模型形式：
-
时间序列模型；
时间序列模型，以
资产收益序列作为被解释变量，描述资产与因子同窗口收益序列之间存在的近似线性关系。
r S , t = α S + ∑ k β S k ⋅ r k , r + ϵ S , t r_{S,t}=\alpha_S + \sum_k\beta^k_S \cdot r_{k,r}+\epsilon_{S,t} rS,t=αS+k∑βSk⋅rk,r+ϵS,t
k k k：因子；r k , t r_{k,t} rk,t：因子 k k k的收益序列（可观测）；
β S k \beta^k_S βSk：资产 S S S对因子 k k k在序列观察窗口内平均的暴露（需要估计）；
-
横截面模型；
横截面模型，以
同期多资产收益作为被解释变量，描述资产下期收益与当期因子暴露之间存在的近似线性关系。 -
时间序列模型与横截面模型的共性
- 都给出了资产收益率、波动（收益率方差）分解的线性、可加形式；
- 都要求解释变量互不相关，即正交化；
-
时间序列模型与横截面模型的区别
- 时间序列模型采用滚动窗口估计方法，因此对资产价格波动的解释相对迟缓
- 横截面模型对不同资产价格波动差异的解释更及时；
- 横截面模型由于不同个股波动率结构有差异，而存在异方差性；
-
-
模型框架
-
横截面因子模型
-
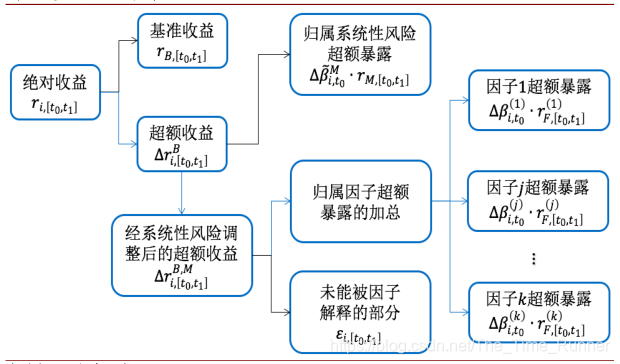
References
- 《基于增量信息逐层解释的因子模型框架搭建》2017.11.22 叶涛、崔浩瀚
扫一扫
3465
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
