激活函数

1）sigmoid

sigmoid的俩个问题：
1.梯度消失。

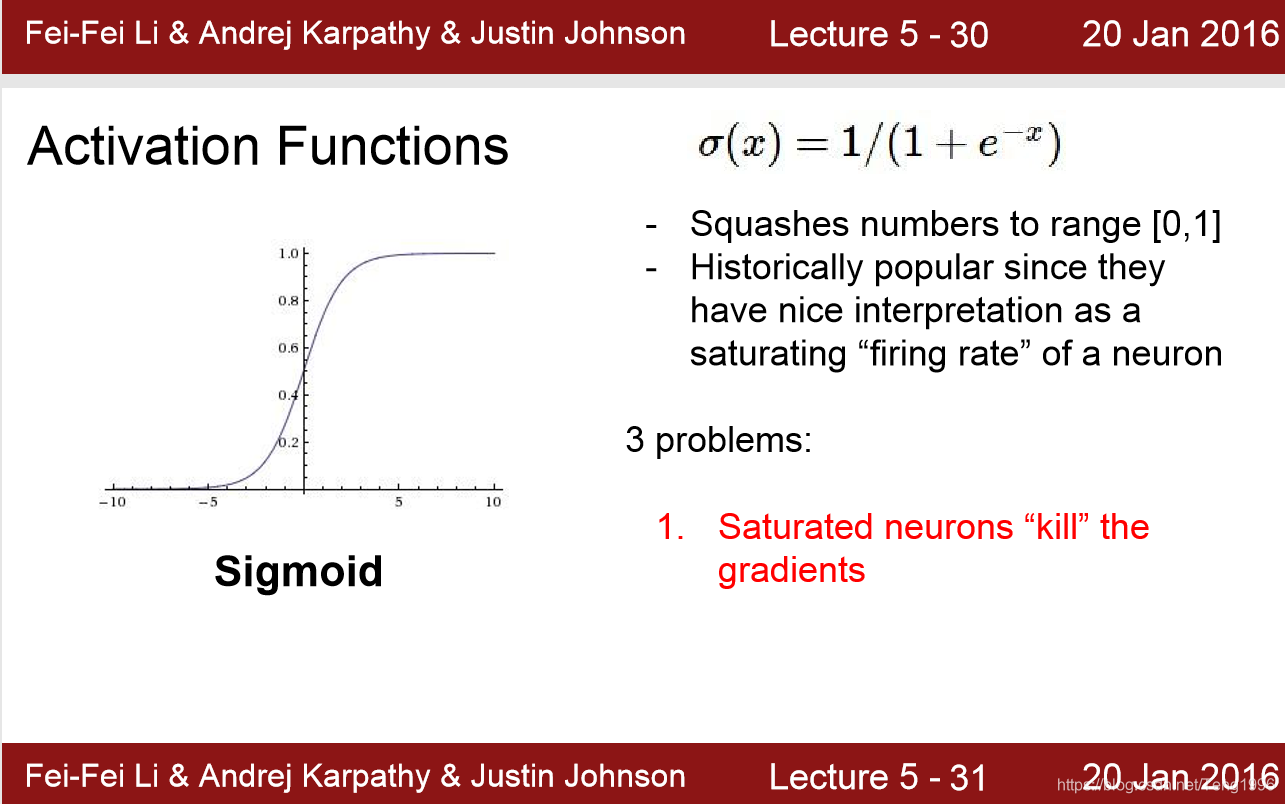
如上图所示，饱和的神经元会kill 梯度。
当x取值为-10和10的时候，$\sigma (x)$对x的导数几乎为0。所以此局部梯度变成了0，不管上游梯度为多少，再利用链式法则求导时，会将损失函数对x的偏度置为0。所以梯度无法继续传递。造成无法进行梯度更新。

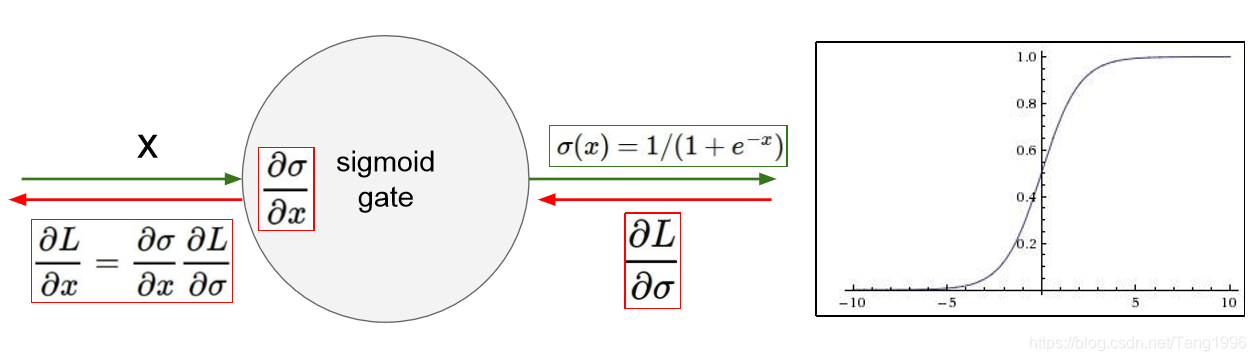
如上图所示，当该神经元达到饱和时(即，经过一定时间训练，输入到该神经元的数据将会远离原点，使得该神经元的输出非0即1，因为这就是训练的初衷)，$\frac{\partial \sigma }{\partial x}$会变为0，这样不管$\frac{\partial L}{\partial \sigma }$为什么值，都会将$\frac{\partial L}{\partial x}$置为0，造成梯度消失。
2.输出不是关于原点对称。

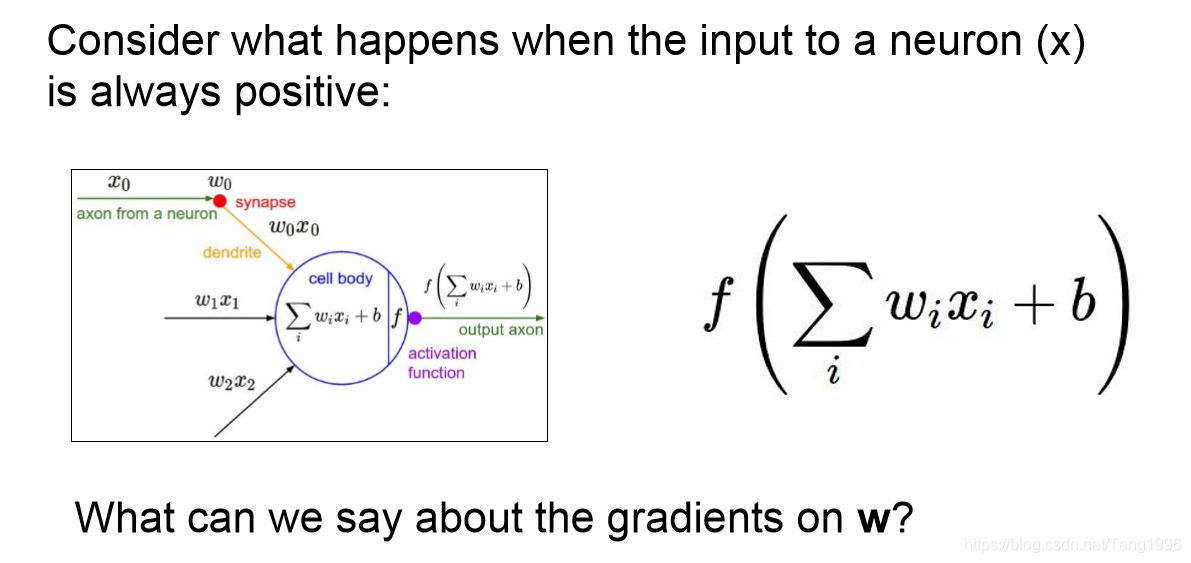这里的f即为sigmoid()函数。考虑到f对$h=\sum _i{w}_i{x}_i+b$的偏导总是正值。所以当上游梯度为正值时，损失函数对h的偏导也为正值。故当$x_i$的值全为正值时（考虑到上一层也可能是sigmoid激活时，其输出值全为正），损失函数对w的偏导也全为正值。
根据经验，当输入数据不是关于原点对称的时候，收敛速度很慢。
下面是一段代码：

import numpy as np
x = np.array([[1,5,3],[2,4,6],[4,8,2],[1,3,5]])
y = np.array([[0,1,1,0]]).T
w1 = np.random.random((3,5))-1
w2 = np.random.random((5,1))-1
for i in range(60000):
    l1 = 1/(1+np.exp(-np.dot(x,w1)))
    l2 = 1/(1+np.exp(-np.dot(l1,w2)))
    loss = np.sum(-(y*np.log(l2)+(1-y)*np.log(1-l2)))
    l2_delta = (l2-y)*(l2*(1-l2))
    l1_delta = l2_delta*(l1*(1-l1))
    l2_delta = (l2-y)*(l2*(1-l2))
    l1_delta = l2_delta*(l1*(1-l1))
    w2 = w2 - l1.T.dot(l2_delta)
    w1 = w1  -x.T.dot(l1_delta)
    if i %1000:
        print('经过了%d次迭代，loss为：%f'%(i,loss))
        print('gradient on w1',x.T.dot(l1_delta))

gradient on w1 [[ 0.00360993  0.00081865  0.00143991 -0.00288004  0.00182933]
 [ 0.01723609  0.00330125  0.00665042  0.01630395  0.00944408]
 [ 0.02164253  0.00383471  0.00800272  0.02268538  0.01032718]]

经过验证，当输入x全为正值时，w1的梯度全为正值.
3.exp() is a bit compute expensive
相比于其他激活函数，进行exp()操作是相对耗时间的。尤其是在卷积神经网络时，计算应该都用来进行卷积操作。

2）tanh

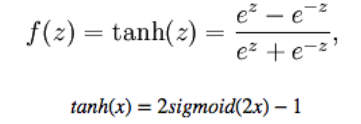
相对于sigmoid()，tanh比较好点，因为它的输出是关于原点对称的。
但还是有梯度消失的问题。

3）relu

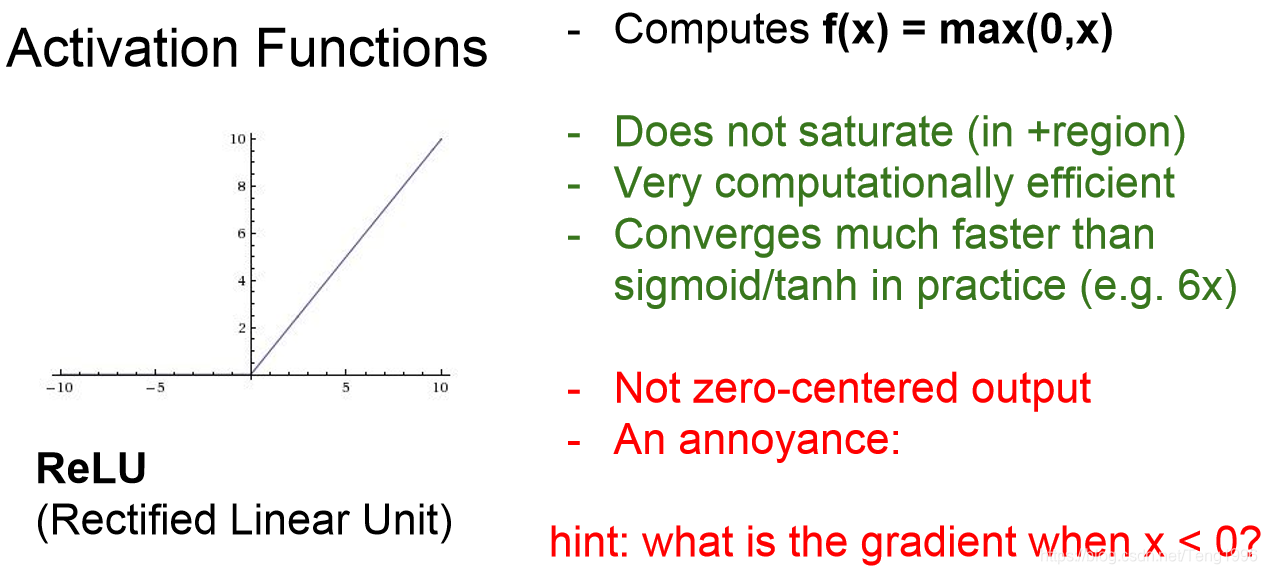
相对于前面的激活函数，这个优点比较明显。
首先，至少一半的梯度不会为0.神经元不会饱和。
问题：
当前向传播时，relu一直处于未激活状态。那么在反向传播时，梯度会消散。
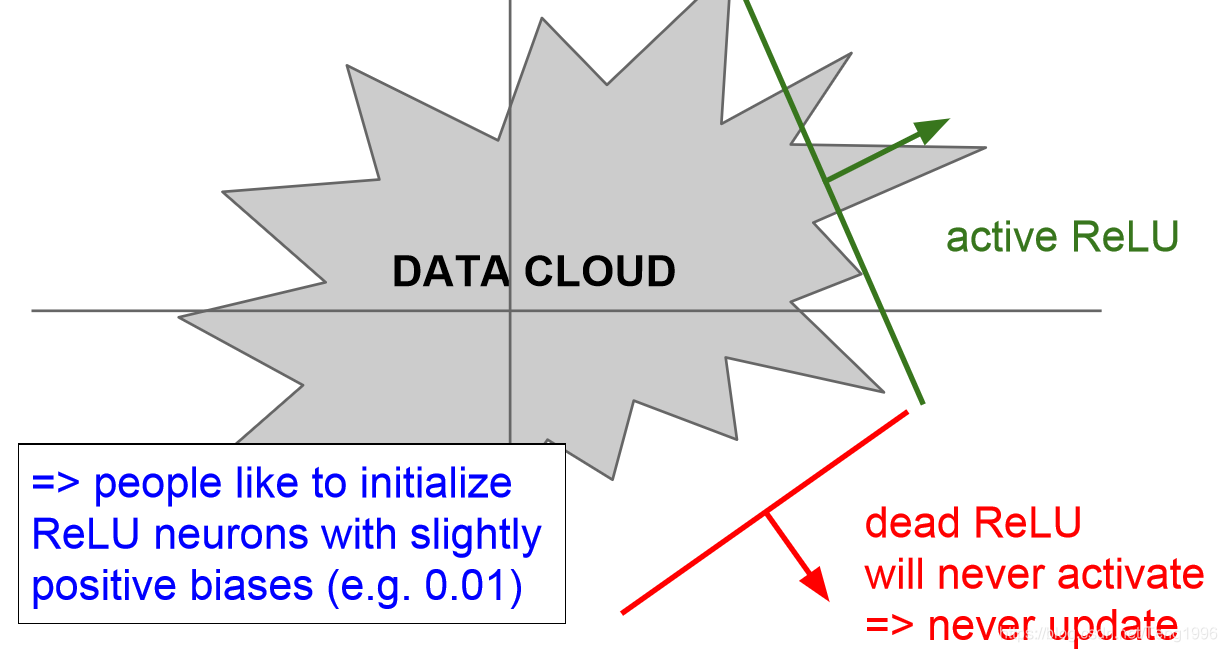一般有两种情况会造成dead relu。
1.在初始化权重时，非常不巧的得到了不能使relu激活的输入。但是这种情况不是很常见
2.另一种是学习率过大的时候，神经元在一定范围内波动，发生数据多样性的消失。这样会使一些神经元永久失活。这种情况比较常见。
针对relu还有一些改进的激活函数。比如Leaky Relu，Elu。

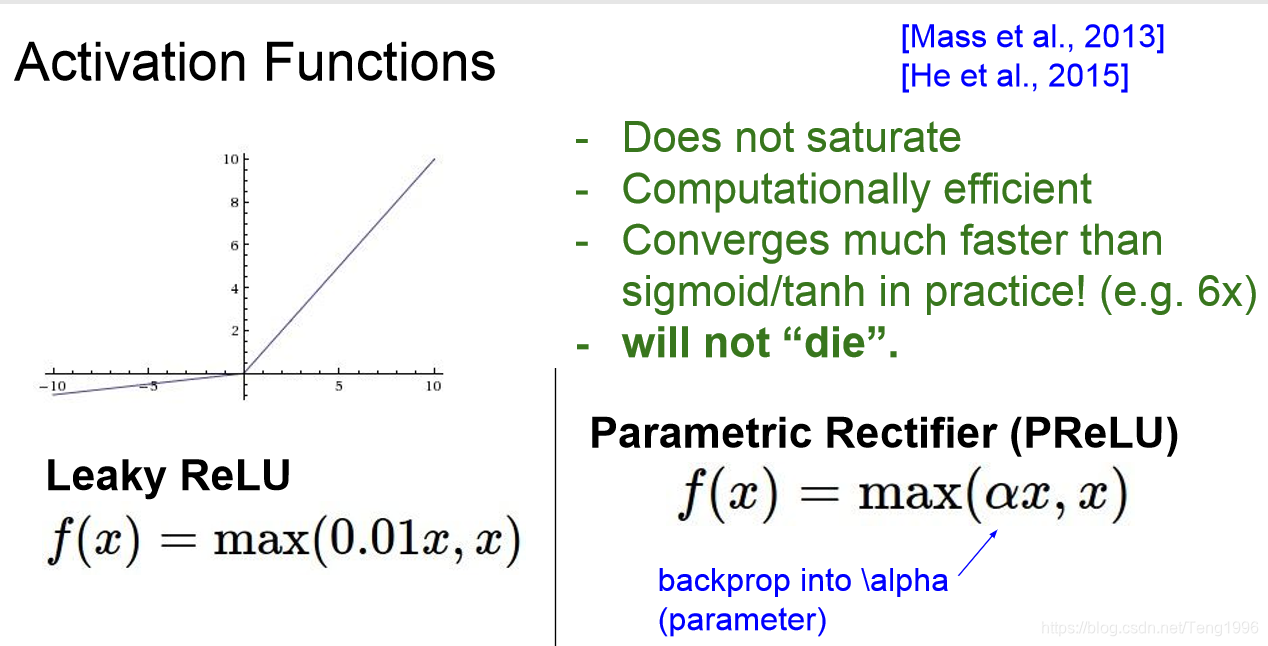
总结

在实际使用中，需要注意的问题：

感觉上面的建议是对于隐层使用的。因为在逻辑回归中，一般都会使用sigmoid作为最后的激活函数，使得输出都被map到[0,1]之间作为概率。