[DataAnalysis]支持向量机的软间隔与正则化

最新推荐文章于 2023-07-08 14:41:58 发布

原创最新推荐文章于 2023-07-08 14:41:58 发布 · 2.7w 阅读

·

0

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

数据分析专栏收录该内容

47 篇文章

订阅专栏

本文探讨了支持向量机(SVM)从理想化的硬间隔转向更为实用的软间隔的概念转变。在现实世界的数据集中，找到能够完全线性分离各类别的核函数通常是不可能的，甚至如果找到了这样的核函数，也可能是因为过拟合。为了解决这个问题，SVM引入了软间隔的概念，允许某些样本点违反分类边界，通过引入松弛变量和惩罚系数，以最小化错误分类的样本数量同时保持最大间隔。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

由硬间隔转为软间隔

理想化的支持向量机存在一个超平面将不同类的样本完全划分开。然而在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中完全线性可分。退一步说，即便恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合造成的。

因此缓解该问题的办法是允许支持向量机在某些样本上出错，为此要引入“软间隔”的概念。如下图所示：

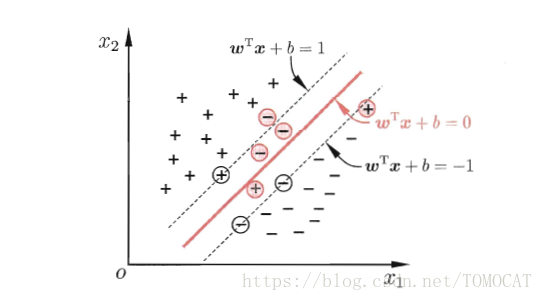
即允许某些样本不满足约束 $y_i(w^Tx_i+b)\geq 1$

优化目标函数

在最大化间隔的同时，我们需要不满足约束的样本点尽可能少，于是优化目标可以写成：

$\min_{w,b}\quad \frac{1}{2}||w||^2+C\sum_{i=1}^{m}l _{0/1}(y_i(w^Tx_i+b)-1)$

其中 $C$ 是一个常数， $l_{0/1}$ 是一个损失函数

$l_{0/1}(z)=\left\{\begin{matrix} 1, & ifz<0\\ 0,& otherwise \end{matrix}\right.$

但是由于 $l_{0/1}$ 非凸，非连续，数学性质不太好，使得参数不容易直接求解。于是人们通常用其他一些函数来代替 $l_{0/1}$ ，称为“替代损失”。常见的替代损失函数有：

损失函数	公式
hinge损失函数	$l_{hinge}(z)=\max(0,1-z)$
指数损失函数	$l_{exp}(z)=exp(-z)$
对率损失函数	$l_{log}(z)=log(1+exp(-z))$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。