DeepSeek-MLA 是什么？

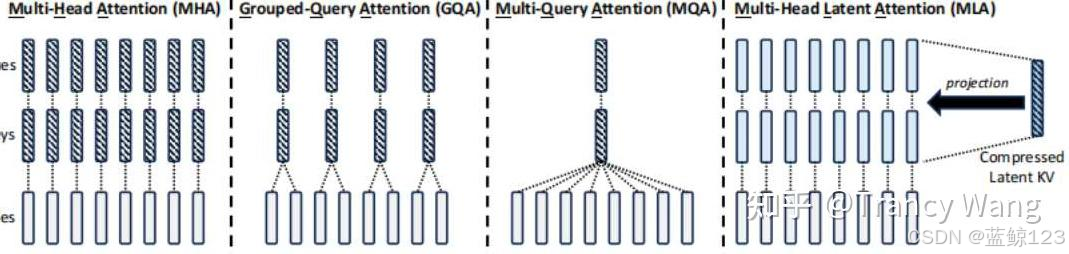
MLA （多头潜注意力，Multi-HeadLatentAttention）

现规定几个变量啊

d: 嵌入维度（Embedding dimension），表示词向量的维度。
nh: 注意力头的数量（Number of attention heads）。
dh: 每个注意力头的维度（Dimension per head）。
ht: 第t个token在某个注意力层的输入（Attention input for the t-th token）。

MLA 的核心思路

1. 先对 token 的特征进行一个“低秩”或“小维度”的压缩（称为 latent vector），再通过少量的变换将它还原/扩展到各头所需要的 Key、Value 空间。
2. 一部分必要的信息（如旋转位置编码 RoPE）的矩阵则保持单独处理，让网络依然能保留时序、位置信息。

首先定义一个矩阵潜注意力W^{DKV}
你就理解成一个下投影的矩阵，维度是 d x d_c，d_c是非常小的。原始肯定是dh*nh啊,也就是每个头的hidden_size,也可以说embedding size。

第t个token在某个hidden_layer的输出你经过我刚才说的下投影矩阵给一压缩，那就变得非常小了

c_t^{KV} = W^{DKV} h_t

_c 表示压缩后的维度，远小于 d_h * n_h，所以你kv对就小了呗，因为小了，所以占显存也少了，推理的时候kv_cache也少，推的也快。

当然你肯定还得逆向把你压缩的回复到原来的维度，那就乘一个上矩阵，要不也推不了么，可以简单认为存的时候存这玩意c_t^{KV} （不占空间），用的时候还得矩阵乘一个上矩阵来还原。

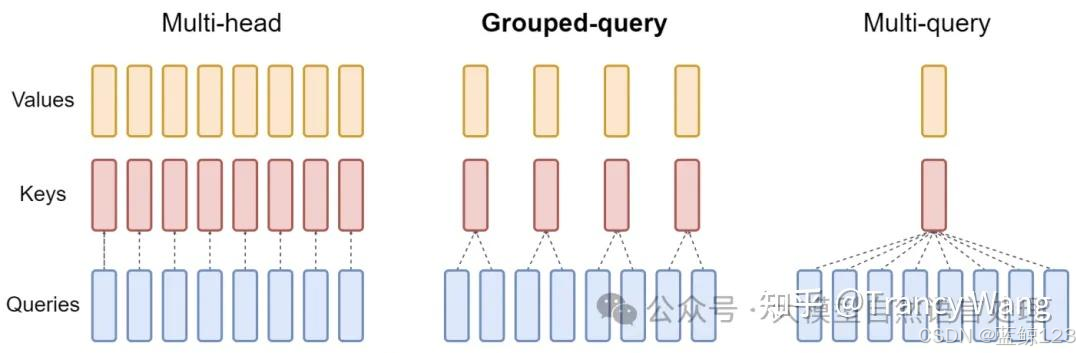
MHA、MQA、MLA

MHA计算复杂度

头的个数是n, 头的大小是m， d = n *m
假设 Q, K ,V的投影矩阵是 [d, m]

对于输入[s, d] 分别进行Q， K，V 投影
所有header的单个投影的Q计算复杂度：

 s * d * 2 * m  = 2dsm = 2nsd^2

Q， K， V投影的复杂度：

6nsd^2

需要保存的中间状态的k，v大小：
2sm*n

GQA

分组查询注意力（GQA）是对 MQA 的进一步改进，介于 MHA 和 MQA 之间，通过分组的方式在效率和表现之间取得平衡。

核心思想：
将多个 Query 分组，每组共享一组 Key 和 Value。通过减少 Key 和 Value 的数量，降低计算复杂度，同时保持多样性。

对于MQA，K，V的个数变小了，共享K， V，所以单个token需要保存的KV数也变小了。所以同样GQA也是减少了KV数。

MQA需要保存的中间状态的k，v大小：
2表示字节的大小

2*s*m

MGA需要保存的中间状态的k，v大小：

2*s*m * G 
G是Group的个数。

MLA