本文深入探讨了多项算法竞赛题目，包括二次方程求解、背包加密系统、人际关系网络分析、竹子切割策略及对称绘画问题。通过具体实例解析，提供高效算法实现思路，如二次剩余法、折半搜索、并查集维护、主席树更新及函数图像叠加等高级技巧。
传送门
B.Quadratic equation
解：没参与讨论
，分析一波，用二次剩余即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p = 1e9+7;
ll w;
struct num {
ll x,y;
};
num mul(num a,num b,ll p) {
num ans= {0,0};
ans.x=((a.x*b.x%p+a.y*b.y%p*w%p)%p+p)%p;
ans.y=((a.x*b.y%p+a.y*b.x%p)%p+p)%p;
return ans;
}
ll powwR(ll a,ll b,ll p) {
ll ans=1;
while(b) {
if(b&1)ans=1ll*ans%p*a%p;
a=a%p*a%p;
b>>=1;
}
return ans%p;
}
ll powwi(num a,ll b,ll p) {
num ans= {1,0};
while(b) {
if(b&1)ans=mul(ans,a,p);
a=mul(a,a,p);
b>>=1;
}
return ans.x%p;
}
ll solve(ll n,ll p) {
n%=p;
if(p==2)return n;
if(powwR(n,(p-1)/2,p)==p-1)return -1;//不存在
ll a;
while(1) {
a=rand()%p;
w=((a*a%p-n)%p+p)%p;
if(powwR(w,(p-1)/2,p)==p-1)break;
}
num x= {a,1};
return powwi(x,(p+1)/2,p);
}
int main() {
srand(time(0));
int t;
scanf("%d",&t);
while(t--) {
long long x[5] = {0},y[5] = {0};
ll b,c;
scanf("%lld%lld",&b,&c);
ll ans3 = b;
ll ans4 = b+p;
ll n = b*b-4*c;
if(n==0) {
if(ans3%2==0) printf("%lld %lld\n",ans3/2,ans3/2);
else if(ans4%2==0) printf("%lld %lld\n",ans4/2,ans4/2);
continue;
}
ll ans1=solve(n,p);
ll ans2=p-ans1;
if(ans1>ans2) swap(ans1,ans2);
if(ans1<0 || ans2<0 || ans3<0 || ans4<0) {
printf("-1 -1\n");
continue;
}
int cnt = 0;
x[++cnt] = (ans1+ans3)%2==0 ? (ans1+ans3)/2 : -1;
x[++cnt] = (ans1+ans4)%2==0 ? (ans1+ans4)/2 : -1;
x[++cnt] = (ans2+ans3)%2==0 ? (ans2+ans3)/2 : -1;
x[++cnt] = (ans2+ans4)%2==0 ? (ans2+ans4)/2 : -1;
cnt = 0;
y[++cnt] = (ans3-ans1)%2==0 ? (ans3-ans1)/2 : -1;
y[++cnt] = (ans3-ans2)%2==0 ? (ans3-ans2)/2 : -1;
y[++cnt] = (ans4-ans1)%2==0 ? (ans4-ans1)/2 : -1;
y[++cnt] = (ans4-ans2)%2==0 ? (ans4-ans2)/2 : -1;
long long ansx,ansy;
bool found = false;
for(int i=1; i<=4; i++) {
for(int j=1; j<=4; j++) {
if(x[i]>=0 && y[j]>=0 && x[i]<p && y[j]<p && (x[i]+y[j])%p==b && x[i]*y[j]%p==c) {
ansx = x[i];
ansy = y[j];
found = true;
}
}
}
if(found) {
if(ansx>ansy) swap(ansx,ansy);
printf("%lld %lld\n",ansx,ansy);
}
if(!found) printf("-1 -1\n");
}
}D.Knapsack Cryptosystem
题意：给你一堆数，选出一些数的和为s，求解方案输出。
解：36直接搜索剪枝肯定是会T的，折半搜索，直接暴力二进制枚举就可以了。
#include<bits/stdc++.h>
#define il inline
#define pb push_back
#define ms(_data,v) memset(_data,v,sizeof(_data))
#define SZ(a) int((a).size())
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int mod=1000000007;
const int maxn=1e6+5;
//il int Add(ll &x,ll y) {return x=x+y>=mod?x+y-mod:x+y;}
//il int Mul(ll &x,ll y) {return x=x*y>=mod?x*y%mod:x*y;}
ll n,s,b[maxn],a[40];
unordered_map<ll,string> sum;
int main() {
scanf("%lld%lld",&n,&s);
for(int i=1; i<=n; ++i) scanf("%lld",&a[i]);
int cnt=0,bit;
for(int i=(n+1)/2+1;i<=n;++i) b[++cnt]=a[i];
bit=(1<<(cnt));
ll ns;
string ss;
for(int i=0;i<bit;++i){
ns=0,ss="";
for(int j=cnt-1;j>=0;--j){
if((i>>j)&1) ns+=b[cnt-j],ss+="1";
else ss+="0";
}
sum[ns]=ss;
}
int pcnt=n-cnt;
bit=(1<<(pcnt));
for(int i=0;i<bit;++i){
ns=0,ss="";
for(int j=pcnt-1;j>=0;--j){
if((i>>j)&1) ns+=a[pcnt-j],ss+="1";
else ss+="0";
}
if(sum.count(s-ns)!=0){
cout<<ss<<sum[s-ns]<<endl;
break;
}
}
return 0;
}
E.All men are brothers
题意：n个人，m次交朋友，每次都要询问所有人中选出4个人互不是朋友的方案数。
解：朋友关系用并查集维护就行了，一开始答案为C(n,2),每次交朋友，如果还不是朋友，那么SZ【U】和SZ【V】中出现在一起将会不合法，我们现在其余的n-sz[U]-sz[V]选出两个组成不合法，但是要减去在其他同一个块中取两个的方案数，这就是这次合并所以不在合法的了，减去。用一个sum取维护所有块中取两个的方案数即可。
#include<bits/stdc++.h>
#define il inline
#define pb push_back
#define ms(_data,v) memset(_data,v,sizeof(_data))
#define SZ(a) int((a).size())
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int N=1e5+5;
int fa[N];
ll sz[N];
int find(int x) {
if(fa[x]==x) return x;
else return fa[x]=find(fa[x]);
}
int main() {
ll n,m;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=n;i++) sz[i]=1;
ll tot=n,sum=0;
ll ans=(unsigned long long)n*(n-1)/2*(n-2)/3*(n-3)/4;
printf("%lld\n",ans);
for(int i=1;i<=m;i++) {
int u,v;
scanf("%d%d",&u,&v);
int U=find(u);
int V=find(v);
if(U==V) {
printf("%lld\n",ans);
continue;
}
else {
tot--;
if(tot<4) ans=0;
else {
ll cnt=n-sz[U]-sz[V];
cnt=(cnt-1)*cnt/2;
sum-=(sz[U]*(sz[U]-1)/2);
sum-=(sz[V]*(sz[V]-1)/2);
cnt-=sum;
ans-=sz[U]*sz[V]*(cnt);
sum+=(sz[U]+sz[V])*(sz[U]+sz[V]-1)/2;
sz[U]+=sz[V];
fa[V]=U;
}
printf("%lld\n",ans);
}
}
return 0;
}H.Cutting Bamboos
题意：砍竹子，给出所有竹子的高度，有q次查询，l,r,x,y,就是对于l，r区间的竹子要用y次砍完，而且每次砍掉的长度要是一样的，求第x砍竹子的高度。
解：先用主席数维护高度在【l,r】 竹子的总高度和个数。查询二分x的高度mid即可（不晓得怎么直接算），看看高度为mid时能否砍掉x次需要砍掉的高度即可。
#include<bits/stdc++.h>
#define il inline
#define pb push_back
#define ms(_data,v) memset(_data,v,sizeof(_data))
#define SZ(a) int((a).size())
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const double eps=1e-7;
const int maxn=2e5+5;
//il int Add(ll &x,ll y) {return x=x+y>=mod?x+y-mod:x+y;}
//il int Mul(ll &x,ll y) {return x=x*y>=mod?x*y%mod:x*y;}
struct node{
ll sum,num;
}tr[maxn*20];
int tot=0,ls[maxn*20],rs[maxn*20],rt[maxn];
il void build(int &rt,int l,int r){
rt=++tot;
tr[rt].sum=tr[rt].num=0;
if(l==r) return ;
int mid=(l+r)>>1;
build(ls[rt],l,mid);
build(rs[rt],mid+1,r);
}
il void update(int &rt,int l,int r,int pre,int h){
rt=++tot;
ls[rt]=ls[pre],rs[rt]=rs[pre];
tr[rt].num=tr[pre].num+1;
tr[rt].sum=tr[pre].sum+h;
if(l==r) return;
int mid=(l+r)>>1;
if(h<=mid) update(ls[rt],l,mid,ls[pre],h);
else update(rs[rt],mid+1,r,rs[pre],h);
}
ll ss,nn;
il void query(int x,int y,int l,int r,int nh){
if(l>=nh){
ss+=tr[y].sum-tr[x].sum;
nn+=tr[y].num-tr[x].num;
return ;
}
int mid=(l+r)>>1;
if(nh<=mid){
ss+=tr[rs[y]].sum-tr[rs[x]].sum;
nn+=tr[rs[y]].num-tr[rs[x]].num;
query(ls[x],ls[y],l,mid,nh);
}
else query(rs[x],rs[y],mid+1,r,nh);
}
int n,q,h[maxn],mx=100000;
ll s[maxn];
int main(){
std::ios::sync_with_stdio(0);
scanf("%d%d",&n,&q);
for(int i=1;i<=n;++i){
scanf("%d",&h[i]);
s[i]=s[i-1]+h[i];
}
build(rt[0],1,mx);
for(int i=1;i<=n;++i) update(rt[i],1,mx,rt[i-1],h[i]);
int l,r,x,y;
for(int i=1;i<=q;++i){
scanf("%d%d%d%d",&l,&r,&x,&y);
double le=0.0,ri=mx*1.0,ans=0.0;
double solve=1.0*(s[r]-s[l-1])/y*x;
while(fabs(ri-le)>eps){
double mid=(le+ri)/2;
int mh=ceil(mid);
ss=0,nn=0;
query(rt[l-1],rt[r],1,mx,mh);
if(1.0*ss-1.0*nn*mid>solve){
le=mid+eps;
ans=mid;
}
else ri=mid-eps;
}
printf("%.15lf\n",ans);
}
return 0;
}J.Symmetrical Painting
题意：很多黑色竖条，你可以选择把任意的部分涂白，使得最后剩下的部分有水平对称轴。
解：有0.5的存在，将L，R全都拉长两倍先。全部看成横条，放在xy轴上看好了，用函数y=kx+b来表示当对称轴为x时，面积为x。考虑只有一根横线的时候，那他的函数图像就是一个山形的，最大值在中间，而且斜率为1的-1，因为当达到中间的时候面积就是黑条的实际长度，即现在黑条长的一半，好理解。而有很多黑条那就时多个一次函数的叠加。而且可能的极值就可能出现在每个黑条的左端点，中间和右端点。函数叠加如下图：
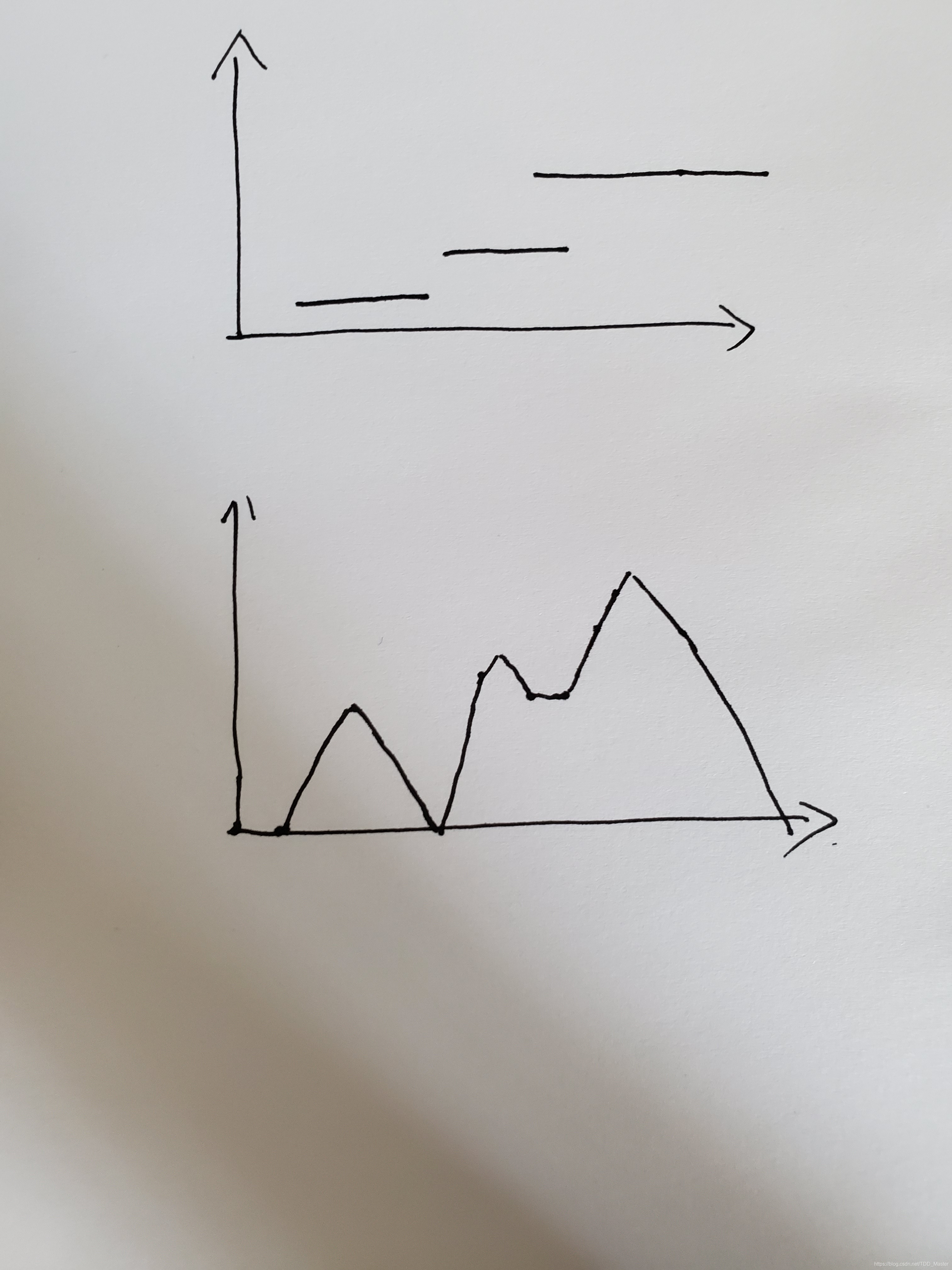
端点处，用1，-2，1来维护现在的斜率即可。
#include<bits/stdc++.h>
#define il inline
#define pb push_back
#define ms(_data,v) memset(_data,v,sizeof(_data))
#define SZ(a) int((a).size())
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int maxn=3e5+5;
//il int Add(ll &x,ll y) {return x=x+y>=mod?x+y-mod:x+y;}
//il int Mul(ll &x,ll y) {return x=x*y>=mod?x*y%mod:x*y;}
struct node{
ll x,k;
}s[maxn*3];
bool cmp(node x,node y) {return x.x<y.x;}
int main(){
int cnt=0,L,R,n;
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d%d",&L,&R);
s[++cnt]=node{L*2,1};
s[++cnt]=node{L+R,-2};
s[++cnt]=node{R*2,1};
}
sort(s+1,s+cnt+1,cmp);
ll px=0,nk=0,ans=0,tp=0;
for(int i=1;i<=cnt;++i){
if(i==1) px=s[i].x,nk+=s[i].k;
else{
tp+=nk*(s[i].x-px);
nk+=s[i].k,px=s[i].x;
ans=max(tp,ans);
}
}
printf("%lld\n",ans);
return 0;
}
扫一扫
1613
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
