题目:计算二重积分 ∫01dx∫0xex+ydy\int_{0}^{1}dx\int_{0}^{\sqrt{x}}e^{x+y}dy∫01dx∫0xex+ydy,并交换积分次序。
解题步骤:
-
确定原积分的积分区域:
原积分的积分区域是由曲线 y=xy = \sqrt{x}y=x,x=0x = 0x=0,x=1x = 1x=1 和 y=0y = 0y=0 所围成的。这个区域可以描述为 D={(x,y)∣0≤x≤1,0≤y≤x}D = \{(x, y) | 0 \leq x \leq 1, 0 \leq y \leq \sqrt{x}\}D={(x,y)∣0≤x≤1,0≤y≤x}。 -
绘制积分区域:
在坐标系中绘制出曲线 y=xy = \sqrt{x}y=x,以及 x=0x = 0x=0,x=1x = 1x=1 和 y=0y = 0y=0。可以看出,积分区域是一个由这些线围成的上半部分抛物线形状的区域。

-
计算原积分:
首先计算原积分 ∫01dx∫0xex+ydy\int_{0}^{1}dx\int_{0}^{\sqrt{x}}e^{x+y}dy∫01dx∫0xex+ydy。这个积分可能需要一些技巧或者数值方法来求解,但在这里我们主要关注交换积分次序的部分,因此不详细展开计算。
-
交换积分次序:
为了交换积分次序,我们需要找到新的积分变量的范围。观察积分区域,我们发现当 yyy 从 000 变化到 111 时,对应的 xxx 的取值范围是从 y2y^2y2 到 111。因此,交换积分次序后的积分可以表示为:∫01dy∫y21ex+ydx\int_{0}^{1}dy\int_{y^{2}}^{1}e^{x+y}dx∫01dy∫y21ex+ydx
-
计算新积分:
现在计算交换积分次序后的积分。这个积分同样可能需要一些技巧或者数值方法来求解。
-
比较结果:
最后,比较原积分和新积分的结果是否相同。由于这两个积分描述的是同一个积分区域,并且被积函数也相同,因此理论上它们的结果应该是一致的。
注意:在实际计算中,可能会遇到一些复杂的积分表达式,需要利用积分技巧或者数值方法来解决。此外,交换积分次序的目的是为了简化计算或者解决某些难以直接计算的问题,因此在实际应用中需要根据具体情况来判断是否进行交换。
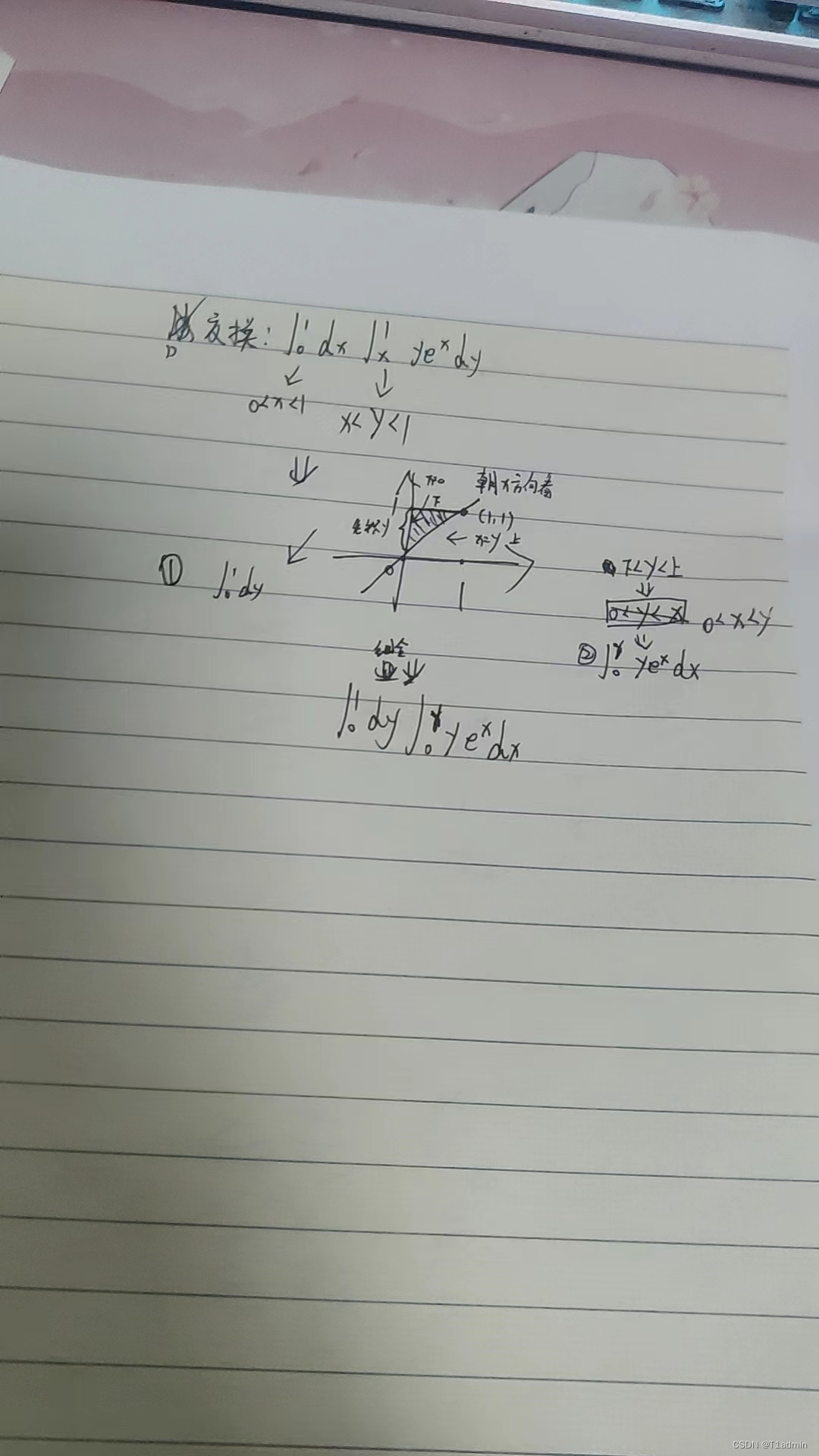





 本文详细解释了如何计算二重积分∫01dx∫0√xe^xdy,并演示了如何通过交换积分次序简化问题。积分区域是一个上半抛物线,通过观察发现新的积分变量范围,将原积分转化为∫01dy∫y21e^xdx,以求解过程和可能用到的技巧为主。
本文详细解释了如何计算二重积分∫01dx∫0√xe^xdy,并演示了如何通过交换积分次序简化问题。积分区域是一个上半抛物线,通过观察发现新的积分变量范围,将原积分转化为∫01dy∫y21e^xdx,以求解过程和可能用到的技巧为主。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








